Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Laboratory evidence for proton energization by collisionless shock surfing

Nature Physics volume 17, pages 1177–1182 (2021)Cite this article

Subjects

Abstract

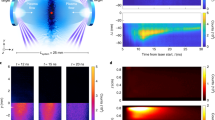
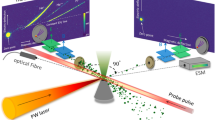
Charged particles can be accelerated to high energies by collisionless shock waves in astrophysical environments, such as supernova remnants. By interacting with the magnetized ambient medium, these shocks can transfer energy to particles. Despite increasing efforts in the characterization of these shocks from satellite measurements at Earth’s bow shock as well as powerful numerical simulations, the underlying acceleration mechanism or a combination thereof is still widely debated. Here we show that astrophysically relevant super-critical quasi-perpendicular magnetized collisionless shocks can be produced and characterized in the laboratory. We observe the characteristics of super-criticality in the shock profile as well as the energization of protons picked up from the ambient gas to hundreds of kiloelectronvolts. Kinetic simulations modelling the laboratory experiment identified shock surfing as the proton acceleration mechanism. Our observations not only provide direct evidence of early-stage ion energization by collisionless shocks but also highlight the role played by this particular mechanism in energizing ambient ions to feed further stages of acceleration. Furthermore, our results open the door to future laboratory experiments investigating the possible transition to other mechanisms, when increasing the magnetic field strength, or the effect that induced shock front ripples could have on acceleration processes.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Configuration and characterization of the laboratory-created super-critical shock.
Fig. 2: Laboratory characterization of electron and ion temperature in the shock.
Fig. 3: Evidence for the energization of protons picked up from the ambient medium.
Fig. 4: Dynamics of the shock surfing proton energization from PIC simulations.

Similar content being viewed by others

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper. Experimental data and simulations are archived on the servers at LULI and LERMA laboratories, respectively, and are available from the corresponding author upon reasonable request.

Code availability

The code used to generate the data shown in Fig. 1b is created using FLASH. The code used to generate a part of Figs. 3 and 4 is created using SMILEI. Both codes are detailed in Methods.

References

  1. Helder, E. A. et al. Measuring the cosmic-ray acceleration efficiency of a supernova remnant. Science 325, 719–722 (2009).

    Article  ADS  Google Scholar 

  2. Turner, D. L. et al. Autogenous and efficient acceleration of energetic ions upstream of earth’s bow shock. Nature 561, 206–210 (2018).

    Article  ADS  Google Scholar 

  3. Decker, R. et al. Mediation of the solar wind termination shock by non-thermal ions. Nature 454, 67–70 (2008).

    Article  ADS  Google Scholar 

  4. Caprioli, D. & Spitkovsky, A. Simulations of ion acceleration at non-relativistic shocks. I. Acceleration efficiency. Astrophys. J. 783, 91–108 (2014).

    Article  ADS  Google Scholar 

  5. Reynoso, E. M., Hughes, J. P. & Moffett, D. A. On the radio polarization signature of efficient and inefficient particle acceleration in supernova remnant SN 1006. Astron. J. 145, 104–113 (2013).

    Article  ADS  Google Scholar 

  6. Burrows, R., Zank, G., Webb, G., Burlaga, L. & Ness, N. Pickup ion dynamics at the heliospheric termination shock observed by Voyager 2. Astrophys. J. 715, 1109–1116 (2010).

    Article  ADS  Google Scholar 

  7. Zank, G., Heerikhuisen, J., Pogorelov, N., Burrows, R. & McComas, D. Microstructure of the heliospheric termination shock: implications for energetic neutral atom observations. Astrophys. J. 708, 1092–1106 (2009).

    Article  ADS  Google Scholar 

  8. Chalov, S., Malama, Y., Alexashov, D. & Izmodenov, V. Acceleration of interstellar pickup protons at the heliospheric termination shock: Voyager 1/2 energetic proton fluxes in the inner heliosheath. Mon. Not. R. Astron. Soc. 455, 431–437 (2016).

    Article  ADS  Google Scholar 

  9. Coroniti, F. Dissipation discontinuities in hydromagnetic shock waves. J. Plasma Phys. 4, 265–282 (1970).

    Article  ADS  Google Scholar 

  10. Edmiston, J. & Kennel, C. A parametric survey of the first critical Mach number for a fast MHD shock. J. Plasma Phys. 32, 429–441 (1984).

    Article  ADS  Google Scholar 

  11. Blandford, R. & Eichler, D. Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154, 1–75 (1987).

    Article  ADS  Google Scholar 

  12. Balogh, A. & Treumann, R. A. Physics of Collisionless Shocks: Space Plasma Shock Waves (Springer, 2013).

  13. Marcowith, A. et al. The microphysics of collisionless shock waves. Rep. Prog. Phys. 79, 046901 (2016).

    Article  ADS  Google Scholar 

  14. Shapiro, V. D. & Üçer, D. Shock surfing acceleration. Planet. Space Sci. 51, 665–680 (2003).

    Article  ADS  Google Scholar 

  15. Yang, Z., Lembège, B. & Lu, Q. Impact of the rippling of a perpendicular shock front on ion dynamics. J. Geophys. Res. Space Phys. 117, A07222 (2012).

    Article  ADS  Google Scholar 

  16. Zank, G., Pauls, H., Cairns, I. & Webb, G. Interstellar pickup ions and quasi-perpendicular shocks: implications for the termination shock and interplanetary shocks. J. Geophys. Res. Space Phys. 101, 457–477 (1996).

    Article  ADS  Google Scholar 

  17. Lee, M. A., Shapiro, V. D. & Sagdeev, R. Z. Pickup ion energization by shock surfing. J. Geophys. Res. Space Phys. 101, 4777–4789 (1996).

    Article  ADS  Google Scholar 

  18. Lembège, B. et al. Selected problems in collisionless-shock physics. Space Sci. Rev. 110, 161–226 (2004).

    Article  ADS  Google Scholar 

  19. Caprioli, D., Pop, A.-R. & Spitkovsky, A. Simulations and theory of ion injection at non-relativistic collisionless shocks. Astrophys. J. Lett. 798, L28 (2015).

    Article  ADS  Google Scholar 

  20. Schaeffer, D. B. et al. Direct observations of particle dynamics in magnetized collisionless shock precursors in laser-produced plasmas. Phys. Rev. Lett. 122, 245001 (2019).

    Article  ADS  Google Scholar 

  21. Albertazzi, B. et al. Production of large volume, strongly magnetized laser-produced plasmas by use of pulsed external magnetic fields. Rev. Sci. Instrum. 84, 043505 (2013).

    Article  ADS  Google Scholar 

  22. Ellison, D. C., Möbius, E. & Paschmann, G. Particle injection and acceleration at Earth’s bow shock: comparison of upstream and downstream events. Astrophys. J. 352, 376–394 (1990).

    Article  ADS  Google Scholar 

  23. Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W. & Lazarus, A. J. Cool heliosheath plasma and deceleration of the upstream solar wind at the termination shock. Nature 454, 63–66 (2008).

    Article  ADS  Google Scholar 

  24. Burlaga, L. et al. Magnetic fields at the solar wind termination shock. Nature 454, 75–77 (2008).

    Article  ADS  Google Scholar 

  25. Khiar, B. et al. Laser-produced magnetic-Rayleigh-Taylor unstable plasma slabs in a 20 T magnetic field. Phys. Rev. Lett. 123, 205001 (2019).

    Article  ADS  Google Scholar 

  26. Giagkiozis, S., Walker, S. N., Pope, S. A. & Collinson, G. Validation of single spacecraft methods for collisionless shock velocity estimation. J. Geophys. Res. Space Phys. 122, 8632–8641 (2017).

    Article  ADS  Google Scholar 

  27. Baraka, S. Large scale Earth’s bow shock with northern IMF as simulated by PIC code in parallel with MHD model. J. Astrophys. Astron. 37, 14 (2016).

    Article  ADS  Google Scholar 

  28. Hillas, A. M. The origin of ultra-high-energy cosmic rays. Annu. Rev. Astron. Astr. 22, 425–444 (1984).

    Article  ADS  Google Scholar 

  29. Drury, L. O. Origin of cosmic rays. Astropart. Phys. 39, 52–60 (2012).

    Article  ADS  Google Scholar 

  30. Katsouleas, T. & Dawson, J. Unlimited electron acceleration in laser-driven plasma waves. Phys. Rev. Lett. 51, 392–395 (1983).

    Article  ADS  Google Scholar 

  31. Matsukiyo, S. & Scholer, M. Microstructure of the heliospheric termination shock: full particle electrodynamic simulations. J. Geophys. Res. Space Phys. 116, A08106 (2011).

    Article  ADS  Google Scholar 

  32. Rho, J. & Petre, R. Mixed-morphology supernova remnants. Astrophys. J. Lett. 503, L167–L170 (1998).

    Article  ADS  Google Scholar 

  33. Nobukawa, K. K. et al. Neutral iron line in the supernova remnant IC 443 and implications for MeV cosmic rays. Publ. Astron. Soc. Jpn 71, 115 (2019).

    Article  ADS  Google Scholar 

  34. Nava, L. et al. Non-linear diffusion of cosmic rays escaping from supernova remnants—II. Hot ionized media. Mon. Not. R. Astron. Soc. 484, 2684–2691 (2019).

    Article  ADS  Google Scholar 

  35. Okon, H., Imai, M., Tanaka, T., Uchida, H. & Tsuru, T. G. Probing cosmic rays with Fe Kα line structures generated by multiple ionization process. Publ. Astron. Soc. Jpn 72, L7 (2020).

    Article  ADS  Google Scholar 

  36. Phan, V. H. M. et al. Constraining the cosmic ray spectrum in the vicinity of the supernova remnant W28: from sub-GeV to multi-TeV energies. Astron. Astrophys. 635, A40 (2020).

    Article  Google Scholar 

  37. Rigby, A. et al. Electron acceleration by wave turbulence in a magnetized plasma. Nat. Phys. 14, 475–479 (2018).

    Article  Google Scholar 

  38. Li, C. et al. Collisionless shocks driven by supersonic plasma flows with self-generated magnetic fields. Phys. Rev. Lett. 123, 055002 (2019).

    Article  ADS  Google Scholar 

  39. Fiuza, F. et al. Electron acceleration in laboratory-produced turbulent collisionless shocks. Nat. Phys. 16, 916–920 (2020).

    Article  Google Scholar 

  40. Lebedev, S., Frank, A. & Ryutov, D. Exploring astrophysics-relevant magnetohydrodynamics with pulsed-power laboratory facilities. Rev. Mod. Phys. 91, 025002 (2019).

    Article  ADS  Google Scholar 

  41. Fujioka, S. et al. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser. Sci. Rep. 3, 1170 (2013).

    Article  Google Scholar 

  42. Kar, S. et al. Plasma jets driven by ultraintense-laser interaction with thin foils. Phys. Rev. Lett. 100, 225004 (2008).

    Article  ADS  Google Scholar 

  43. Cole, A. J. et al. Measurement of Rayleigh–Taylor instability in a laser-accelerated target. Nature 299, 329–331 (1982).

    Article  ADS  Google Scholar 

  44. Higginson, D. et al. Laboratory investigation of particle acceleration and magnetic field compression in collisionless colliding fast plasma flows. Commun. Phys. 2, 60 (2019).

    Article  Google Scholar 

  45. Higginson, D. et al. Detailed characterization of laser-produced astrophysically-relevant jets formed via a poloidal magnetic nozzle. High Energ. Dens. Phys. 23, 48–59 (2017).

    Article  ADS  Google Scholar 

  46. Froula, D. H., Luhmann Jr., N. C., Sheffield, J. & Glenzer, S. H. Plasma Scattering of Electromagnetic Radiation Theory and Measurement Techniques (Academic Press, 2011).

  47. Froula, D. et al. Quenching of the nonlocal electron heat transport by large external magnetic fields in a laser-produced plasma measured with imaging Thomson scattering. Phys. Rev. Lett. 98, 135001 (2007).

    Article  ADS  Google Scholar 

  48. Faenov, A. Y., Pikuz, S. A., Erko, A. I. & Bryunetkin, B. A. et al. High-performance X-ray spectroscopic devices for plasma microsources investigations. Phys. Scr. 50, 333–338 (1994).

    Article  ADS  Google Scholar 

  49. Ryazantsev, S. N., Skobelev, I. Y., Faenov, A. Y. & Pikuz, T. A. et al. Diagnostics of laser-produced plasmas based on the analysis of intensity ratios of He-like ions X-ray emission. Phys. Plasmas 23, 123301 (2016).

    Article  ADS  Google Scholar 

  50. Mančić, A., Fuchs, J., Antici, P., Gaillard, S. & Audebert, P. Absolute calibration of photostimulable image plate detectors used as (0.5–20 MeV) high-energy proton detectors. Rev. Sci. Instrum. 79, 073301 (2008).

    Article  ADS  Google Scholar 

  51. Fryxell, B. et al. FLASH: an adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys. J. Suppl. Ser. 131, 273–334 (2000).

    Article  ADS  Google Scholar 

  52. Haines, M. Magnetic-field generation in laser fusion and hot-electron transport. Can. J. Phys. 64, 912–919 (1986).

    Article  ADS  Google Scholar 

  53. Atzeni, S. & Meyer-ter Vehn, J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter Vol. 125 (OUP, 2004).

  54. Derouillat, J. et al. SMILEI: a collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 222, 351–373 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  55. Shoji, Y. et al. Toward the generation of magnetized collisionless shocks with high-power lasers. Plasma Fusion Res. 11, 3401031 (2016).

    Article  ADS  Google Scholar 

  56. Decker, R. et al. Voyager 1 in the foreshock, termination shock, and heliosheath. Science 309, 2020–2024 (2005).

    Article  ADS  Google Scholar 

  57. Cosentino, G. et al. Interstellar plunging waves: ALMA resolves the physical structure of nonstationary MHD shocks. Astrophys. J. Lett. 881, L42 (2019).

    Article  ADS  Google Scholar 

  58. Slavin, J. A. & Holzer, R. E. Solar wind flow about the terrestrial planets. 1—Modeling bow shock position and shape. J. Geophys. Res. Space Phys. 86, 11401–11418 (1981).

    Article  ADS  Google Scholar 

  59. Bale, S., Mozer, F. & Horbury, T. Density-transition scale at quasi-perpendicular collisionless shocks. Phys. Rev. Lett. 91, 265004 (2003).

    Article  ADS  Google Scholar 

  60. Liebert, E., Nabert, C. & Glassmeier, K.-H. Statistical survey of day-side magnetospheric current flow using Cluster observations: bow shock. Ann. Geophys. 36, 1073–1080 (2018).

    Article  ADS  Google Scholar 

  61. Stasiewicz, K. & Eliasson, B. Quasi-adiabatic and stochastic heating and particle acceleration at quasi-perpendicular shocks. Astrophys. J. 903, 57 (2020).

    Article  ADS  Google Scholar 

  62. Velàzquez, P. F., Dubner, G. M., Goss, W. M. & Green, A. J. Investigation of the large-scale neutral hydrogen near the supernova remnant W28. Astronom. J. 124, 2145 (2002).

    Article  ADS  Google Scholar 

  63. Hoffman, I. M., Goss, W., Brogan, C. & Claussen, M. The OH (1720 MHz) supernova remnant masers in W28: MERLIN and VLBA polarization observations. Astrophys. J. 620, 257–273 (2005).

    Article  ADS  Google Scholar 

  64. Brogan, C. L. OH (1720 MHz) masers: signposts of SNR/molecular cloud interactions. In Proc. International Astronomical Union 3, 299–306 (IAU, 2007).

  65. Li, H. & Chen, Y. γ-rays from molecular clouds illuminated by accumulated diffusive protons from supernova remnant W28. Mon. Not. R. Astron. Soc. Lett. 409, L35–L38 (2010).

    Article  ADS  Google Scholar 

  66. Abdo, A. et al. Fermi large area telescope observations of the supernova remnant W28 (G6.4–0.1). Astrophys. J. 718, 348–356 (2010).

    Article  ADS  Google Scholar 

  67. Vaupré, S. et al. Cosmic ray induced ionisation of a molecular cloud shocked by the W28 supernova remnant. Astron. Astrophys. 568, A50 (2014).

    Article  Google Scholar 

  68. Okon, H., Uchida, H., Tanaka, T., Matsumura, H. & Tsuru, T. G. The origin of recombining plasma and the detection of the Fe-K line in the supernova remnant W 28. Publ. Astron. Soc. Jpn 70, 35 (2018).

    Article  ADS  Google Scholar 

  69. Miceli, M. et al. XMM-Newton observation of the supernova remnant Kes 78 (G32.8-0.1): evidence of shock-cloud interaction. Astron. Astrophys. 599, A45 (2017).

    Article  Google Scholar 

  70. Boumis, P. et al. Discovery of optical emission from the supernova remnant G 32.8-0.1 (Kes 78). Astron. Astrophys. 499, 789–797 (2009).

    Article  ADS  Google Scholar 

  71. Koralesky, B., Frail, D., Goss, W., Claussen, M. & Green, A. Shock-excited maser emission from supernova remnants: G32.8–0.1, G337.8–0.1, G346.6–0.2, and the HB 3/W3 complex. Astron. J. 116, 1323–1331 (1998).

    Article  ADS  Google Scholar 

  72. Lockett, P., Gauthier, E. & Elitzur, M. OH 1720 megahertz masers in supernova remnants: C-shock indicators. Astrophys. J. 511, 235–241 (1999).

    Article  ADS  Google Scholar 

  73. Frail, D. A. & Mitchell, G. F. OH (1720 MHz) masers as signposts of molecular shocks. Astrophys. J. 508, 690–695 (1998).

    Article  ADS  Google Scholar 

  74. Claussen, M., Frail, D., Goss, W. & Gaume, R. Polarization observations of 1720 MHz OH masers toward the three supernova remnants W28, W44, and IC 443. Astrophys. J. 489, 143–159 (1997).

    Article  ADS  Google Scholar 

  75. Greco, E. et al. Discovery of a jet-like structure with overionized plasma in the SNR IC 443. Astron. Astrophys. 615, A157 (2018).

    Article  Google Scholar 

  76. Cesarsky, D. et al. ISOCAM spectro-imaging of the H2 rotational lines in the supernova remnant IC 443. Astron. Astrophys. 348, 945–949 (1999).

    ADS  Google Scholar 

  77. Reach, W. T., Richter, M., Gusdorf, A. & Dewitt, C. et al. Supernova shocks in molecular clouds: velocity distribution of molecular hydrogen. Astrophys. J. 884, 81 (2019).

    Article  ADS  Google Scholar 

  78. Ghavamian, P., Laming, J. M. & Rakowski, C. E. A physical relationship between electron-proton temperature equilibration and Mach number in fast collisionless shocks. Astrophys. J. Lett. 654, L69–L72 (2006).

    Article  ADS  Google Scholar 

  79. Kaufman, M. J. & Neufeld, D. A. Far-infrared water emission from magnetohydrodynamic shock waves. Astrophys. J. 456, 611–630 (1996).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank the teams of LULI (France) and JLF (USA) laser facilities for their expert support, as well the Dresden High Magnetic Field Laboratory at Helmholtz-Zentrum Dresden-Rossendorf for the development of the pulsed power generator used at LULI. We thank the SMILEI dev team for technical support. We also thank Ph. Savoini (Sorbonne University, France) and L. Gremillet and C. Ruyer (CEA, France) for discussions. W.Y. thanks R. Li (SZTU, China) for discussions. This work was supported by funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement no. 787539; J.F.). The computational resources of this work were supported by the National Sciences and Engineering Research Council of Canada (NSERC), Fonds québécois de la recherche sur la nature et les technologies (FRQNT) - Projet Samuel-de Champlain 293688) and Compute Canada (Job: pve-323-ac; P.A.). Part of the experimental system is covered by a patent (1000183285, 2013, INPI-France). The FLASH software used was developed, in part, by the Flash Center for Computational Science at the University of Chicago supported by the DOE NNSA, ASC, and the DOE Office of Science, ASCR. The research leading to these results is supported by Extreme Light Infrastructure Nuclear Physics (ELI-NP) Phase II, a project co-financed by the Romanian Government and European Union through the European Regional Development Fund (S.N.C., S.K., V.N. and D.C.P.), and by the project ELI-RO-2020-23 funded by IFA, Romania (J.F.). JIHT RAS team members are supported by the Ministry of Science and Higher Education of the Russian Federation (State Assignment No. 075-00460-21-00; E.D.F. and S.P.). The reported study was funded by the Russian Foundation for Basic Research, project no. 19-32-60008 (E.D.F.).

Author information

Authors and Affiliations

  1. LULI–CNRS, CEA, UPMC Univ Paris 06:Sorbonne Université, École Polytechnique, Institut Polytechnique de Paris, Palaiseau, France

    W. Yao, A. Fazzini, K. Burdonov, S. Bolaños, R. Diab, V. Lelasseux, G. Revet & J. Fuchs

  2. Sorbonne Université, Observatoire de Paris, Université PSL, CNRS, LERMA, Paris, France

    W. Yao, K. Burdonov & A. Ciardi

  3. ELI-NP, ‘Horia Hulubei’ National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania

    S. N. Chen, S. Kisyov, V. Nastasa & D. C. Popescu

  4. IAP, Russian Academy of Sciences, Nizhny Novgorod, Russia

    K. Burdonov & E. D. Filippov

  5. INRS-EMT, Varennes, Québec, Canada

    P. Antici

  6. LNCMI, UPR 3228, CNRS-UGA-UPS-INSA, Toulouse, France

    J. Béard

  7. JIHT, Russian Academy of Sciences, Moscow, Russia

    E. D. Filippov & S. Pikuz

  8. Università degli Studi di Palermo, Dipartimento di Fisica e Chimica—Emilio Segrè, Palermo, Italy

    M. Miceli

  9. INAF—Osservatorio Astronomico di Palermo, Palermo, Italy

    M. Miceli & S. Orlando

  10. University of Bordeaux, Centre Lasers Intenses et Applications, CNRS, CEA, UMR 5107, Talence, France

    Q. Moreno, X. Ribeyre & E. d’Humières

  11. ELI Beamlines, Institute of Physics, Czech Academy of Sciences, Dolní Břežany, Czech Republic

    Q. Moreno

  12. NRNU MEPhI, Moscow, Russia

    S. Pikuz

Authors
  1. W. Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Fazzini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. N. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. K. Burdonov
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. P. Antici
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. J. Béard
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. S. Bolaños
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. A. Ciardi
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. R. Diab
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. E. D. Filippov
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. S. Kisyov
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. V. Lelasseux
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. M. Miceli
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Q. Moreno
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. V. Nastasa
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. S. Orlando
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. S. Pikuz
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. D. C. Popescu
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. G. Revet
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. X. Ribeyre
    View author publications

    You can also search for this author in PubMed Google Scholar

  21. E. d’Humières
    View author publications

    You can also search for this author in PubMed Google Scholar

  22. J. Fuchs
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.F. and S.N.C. conceived the project. A.F., S.N.C., K.B., J.B., S.B., S.K., V.L., V.N., S.P., D.C.P., G.R. and J.F. performed the experiments. A.F., E.D.F., S.N.C., K.B., R.D., S.P. and J.F. analysed the data. X.R. performed and analysed the FLASH simulations, while W.Y. and A.F. performed and analysed the SMILEI simulations, both with discussions with P.A., A.C., Q.M., X.R., E.d.H. and J.F. W.Y., S.N.C. and J.F. wrote the bulk of the paper, with major contributions from K.B., M.M. and S.O. All the authors commented and revised the paper.

Corresponding author

Correspondence to J. Fuchs.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Physics thanks Kai Germaschewski and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Table 1 Comparison between the parameters of the shocks
Full size table

Extended Data Fig. 1 X-ray emissivity of Lyα line measured by the FSSR.

The red curve represents the piston plasma emission in the range 0–10 mm in the case when the unmagnetized piston expands in the ambient gas. The black curve represents the same but when additionally, the transverse external magnetic field was applied.

Extended Data Fig. 2 Time sequence of experimental density measurement.

(integrated along the line of sight) recorded in the two different and complementary xy and xz planes in order to characterize in three-dimensions the overall plasma. Each image corresponds to a different laser shot. Specifically, the images shown in panels (a1-a4) correspond to the case without the external magnetic field; the images shown in panels (b1-b4) and (c1-c4) correspond to the case with the external magnetic field, which is aligned along the z-axis, the difference between panels (b1-b4) and (c1-c4) is the direction of the optical probing, which is along the z-axis for panels (b1-b4) and along the y-axis for panels (c1-c4). The color scale shown at the bottom applies to all images. The images shown in panels (d1-d4) correspond to the lineouts along the thin dark lines shown in each images of panels (a1-a4), (b1-b4) and (c1-c4). From top to bottom, each row represents a different time, that is, 2/4/6/8 ns. Magnetic field directions are indicated at the top of each column. Orange and green arrows indicate the piston and the shock front, respectively.

Extended Data Fig. 3 Temporal evolution of the electron temperature.

obtained from the solution of \(1.5{n}_{e}{d}_{t}{T}_{e}={\nu }_{B}{I}_{0}{e}^{-{t}^{2}/{\tau }^{2}}\). Here, ne = 1018 cm−3, νB is the inverse Bremsstrahlung absorption coefficient from the NRL formulary (p.58/Eq.32). The laser energy is 15 J, with duration τ = 3 ns, defocused focal spot d = 200μm and wavelength λl = 528 nm, leading to an maximum intensity of I0 = 1.5 × 1013 W ⋅ cm−2, and the initial electron temperature Te0 = 10 eV (left axis, blue). The intensity evolution of the laser (ITS) is superimposed as a red line (right axis).

Extended Data Fig. 4 Examples of plasma density and temperature measurement of the shock downstream (DS).

(a) Schematic diagram of the collective Thomson scattering (TS) diagnostic deployed at LULI2000. The measurement is performed, in a fixed volume (see Methods) through which the shock is sweeping, 4.3 mm away from the solid target surface, separating the downstream (DS) and upstream (US) regions. Panels (b) and (c) show TS measurement on the ion waves in the plasma, allowing to retrieve the local electron and ion temperatures, as stated. The vertical axis represents the amplitude of the scattered light; the horizontal axis represents the wavelength (λ) of the scattered light. Both measurements are performed 3 ns after the shock has passed, but (b) corresponds to the case without external B-field, while (c) corresponds to the case with B = 20 T applied. Solid lines – experimental data profiles; dashed lines – theoretical spectra, from which we extract the electron plasma density as well as the electron and ion temperatures in the plasma. The stated uncertainties in the retrieved plasma parameters represent the possible variation of the parameters of the theoretical fit, while still fitting well the data, as well as the shot-to-shot variations observed in the same conditions.

Extended Data Fig. 5 Examples of plasma density and temperature measurement upstream (US) and downstream (DS) of the shock.

(a) and (c) Schematic diagram of the collective Thomson scattering (TS) diagnostic deployed at LULI2000. The measurement is performed, in a fixed volume (see Methods) through which the shock is sweeping, 4.3 mm away from the solid target surface. Panel (b) illustrates a TS measurement on the electron waves in the plasma, allowing the retrieve the local electron density and temperature, as stated. The measurement is performed 3 ns before the shock sweeps through (as illustrated in (a)). Panel (d) corresponds to the measurement performed at the same location, 1 ns after the shock has passed (as illustrated in (c)). For both panels (b) and (d), the vertical axis represents the amplitude of the scattered light; the horizontal axis represents the wavelength (λ) of the scattered light. Solid lines – experimental data profiles; dashed lines – theoretical spectra, from which we extract the electron plasma density as well as the electron temperature in the plasma. The stated uncertainties in the retrieved plasma parameters represent the possible variation of the parameters of the theoretical fit, while still fitting well the data, as well as the shot-to-shot variations observed in the same conditions.

Extended Data Fig. 6 Maps of the magnetic field in the MHD simulations.

2 ns after the start of the plasma piston expansion inside the magnetized ambient medium. Shown are two-dimensional cross-section in the (a) xy and (b) xz planes, the latter with the corresponding magnetic field lines. The target is located on the left side of the box and the laser comes from the right side, as in the experiment. The colormap represents the strength of Bz in the unit of Tesla.

Extended Data Fig. 7 Proton phase space evolution in the PIC simulations.

The horizontal axis (x) is the proton position and the vertical axis (vx) is the proton velocity along the x-direction. The first row corresponds to the high-velocity case with initial velocity of 1500 km/s, while the second row is for the low-velocity one with initial velocity of 500 km/s (see text for more details), at (a) & (d) 0.5 ns, (b) & (e) 1.5 ns, and (c) & (f) 2.5 ns. The colorbar represents the normalized particle number N in logarithm scale.

Extended Data Fig. 8 Extended proton energy spectra.

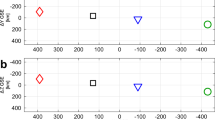
(a) Energy spectrum from the experiment represented by red dots (averaged over 5 shots) with blue error bars (correspond to one sigma deviation from the average), fitted by a power-law function (purple dashed line); together with PIC simulated spectra at t = 2.6 ns (black solid line) and t = 5.1 ns (green solid line). The horizontal axis (Ep) represents the kinetic energy of the protons, while the vertical axis represents the number of protons per bin of energy (dN/dE), divided by the solid angle (dΩ) subtended by the entrance pinhole of the spectrometer (in the case of the experimental spectrum). Note that the absolute scale in proton numbers applies only to the experimental spectrum; the simulated spectra are adjusted to the experimental one. The latter is also fitted by a power-law function (green dashed line). (b) The same experimental data, as well as the simulations with and w/o collisions (green dashed line and black solid line, respectively). (c) Energy spectra of protons in cases of different B-field strength, overlaid on the same experimental data. The B-field strength is varied by varying the angle between the B-field direction (along z) and the on-axis shock propagation direction (along x) in the xz-plane.

Extended Data Fig. 9 Extended PIC simulation results.

(a)-(e) Lineouts of density (ni) and EM fields (Bz, Ey, and Ex), as well as the corresponding phase-space distribution (Vx) at the same position and time as in Fig. 4c in the main paper, that is, from 0.4 mm to 1.2 mm at 1.5 ns, in SI units. (f) Trajectories of six randomly selected protons energized from the ambient gas in the x − t diagram, overlaid on the proton density map in the contact discontinuity reference frame; all this for a simulation run over 5.31 ns, that is, over longer time than the simulation shown in the paper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, W., Fazzini, A., Chen, S.N. et al. Laboratory evidence for proton energization by collisionless shock surfing. Nat. Phys. 17, 1177–1182 (2021). https://doi.org/10.1038/s41567-021-01325-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-021-01325-w

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing