Abstract
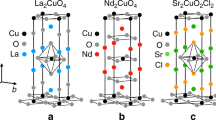
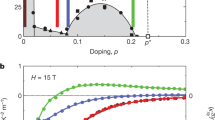
The nature of the pseudogap phase of cuprates remains a major puzzle1,2. One of its signatures is a large negative thermal Hall conductivity3, whose origin is as yet unknown. This is observed even in the undoped Mott insulator La2CuO4, in which the charge carriers are localized and therefore cannot be responsible. Here, we show that the thermal Hall conductivity of La2CuO4 is roughly isotropic; that is, for heat transport parallel and normal to the CuO2 planes, it is nearly the same. This shows that the Hall response must come from phonons, as they are the only heat carriers that are able to move with the same ease both normal and parallel to the planes4. For doping levels higher than the critical doping level at which the pseudogap phase ends, both La1.6−xNd0.4SrxCuO4 and La1.8−xEu0.2SrxCuO4 show no thermal Hall signal for a heat current normal to the planes, which establishes that phonons have zero Hall response outside the pseudogap phase. Inside the pseudogap phase, the phonons must become chiral to generate the Hall response, but the mechanism by which this happens remains to be identified. It must be intrinsic (from a coupling of phonons to their electronic environment) rather than extrinsic (from structural defects or impurities), as these are the same on both sides of critical doping.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
All of the data that support the plots in this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Keimer, B. et al. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Proust, C. & Taillefer, L. The remarkable underlying ground states of cuprate superconductors. Annu. Rev. Condens. Matter Phys. 10, 409–429 (2019).
Grissonnanche, G. et al. Giant thermal Hall conductivity in the pseudogap phase of cuprate superconductors. Nature 571, 376–380 (2019).
Hess, C. et al. Magnon heat transport in doped La2CuO4. Phys. Rev. Lett. 90, 197002 (2003).
Onose, M. et al. Observation of the magnon Hall effect. Science 329, 297–299 (2010).
Katsura, H., Nagaosa, N. & Lee, P. A. Theory of the thermal Hall effect in quantum magnets. Phys. Rev. Lett. 104, 066403 (2010).
Hirschberger, M. et al. Large thermal Hall conductivity of neutral spin excitations in a frustrated quantum magnet. Science 348, 106–109 (2015).
Lee, H., Han, J. H. & Lee, P. A. Thermal Hall effect of spins in a paramagnet. Phys. Rev. B 91, 125413 (2015).
Qin, T., Zhou, J. & Shi, J. Berry curvature and the phonon Hall effect. Phys. Rev. B 86, 104305 (2012).
Yang, Y.-F., Zhang, G.-M. & Zhang, F.-C. Universal behavior of the anomalous thermal Hall conductivity. Phys. Rev. Lett. 124, 186602 (2020).
Nasu, J., Yoshitake, J. & Motome, Y. Thermal transport in the Kitaev model. Phys. Rev. Lett. 119, 127204 (2017).
Ye, M. et al. Quantization of the thermal Hall conductivity at small Hall angles. Phys. Rev. Lett. 121, 147201 (2018).
Vinkler-Aviv, Y. & Rosch, A. Approximately quantized thermal Hall effect of chiral liquids coupled to phonons. Phys. Rev. X 8, 031032 (2018).
Mori, M. et al. Origin of the phonon Hall effect in rare-Earth garnets. Phys. Rev. Lett. 113, 265901 (2014).
Ideue, T. et al. Giant thermal Hall effect in multiferroics. Nat. Mater. 16, 797–802 (2017).
Li, X. et al. Phonon thermal Hall effect in strontium titanate. Phys. Rev. Lett. 124, 105901 (2020).
Samajdar, R. et al. Enhanced thermal Hall effect in the square-lattice Néel state. Nat. Phys. 15, 1290–1294 (2019).
Han, J. H., Park, J.-H. & Lee, P. A. Consideration of thermal Hall effect in undoped cuprates. Phys. Rev. B 99, 205157 (2019).
Chen, J.-Y., Kivelson, S. A. & Sun, X.-Q. Enhanced thermal Hall effect in nearly ferroelectric insulators. Phys. Rev. Lett. 124, 167601 (2020).
Collignon, C. et al. Fermi-surface transformation across the pseudogap critical point of the cuprate superconductor La2−xNd0.4SrxCuO4. Phys. Rev. B 95, 224517 (2017).
Matt, C. E. et al. Electron scattering, charge order and pseudogap physics in La2−xNd0.4SrxCuO4: an angle-resolved photoemission spectroscopy study. Phys. Rev. B 92, 134524 (2015).
Michon, B. et al. Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature 567, 281–222 (2019).
Strohm, C., Rikken, G. L. J. A. & Wyder, P. Phenomenological evidence for the phonon Hall effect. Phys. Rev. Lett. 95, 155901 (2005).
He, Y. et al. Rapid change in superconductivity and electron-phonon coupling through the critical point in Bi-2212. Science 362, 62–65 (2019).
Kyung, B. et al. Pseudogap induced by short-range spin correlations in a doped Mott insulator. Phys. Rev. B 73, 165114 (2006).
Scheurer, M. S. et al. Topological order in the pseudogap metal. Proc. Natl Acad. Sci. USA 115, E3665–E3672 (2018).
Hunt, A. W. et al. Glassy slowing of stripe modulation in (La,Eu,Nd)2−x(Sr,Ba)xCuO4: a 63Cu and 139La NQR study down to 350 mK. Phys. Rev. B 64, 134525 (2001).
Frachet, M. et al. Hidden magnetism at the pseudogap critical point of a high-temperature superconductor. Preprint at https://arxiv.org/abs/1909.10258 (2019).
Ye, M. et al. Phonon dynamics in the Kitaev spin liquid. Preprint at https://arxiv.org/abs/2002.05328 (2020).
Hirokane, Y. et al. Phononic thermal Hall effect in diluted terbium oxides. Phys. Rev. B 99, 134419 (2019).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Hentrich, R. et al. Large thermal Hall effect in α-RuCl3: Evidence for heat transport by Kitaev-Heisenberg paramagnons. Phys. Rev. B 99, 085136 (2019).
Cyr-Choinière, O. et al. Pseudogap temperature T* of cuprate superconductors from the Nernst effect. Phys. Rev. B 97, 064502 (2018).
Grissonnanche, G. et al. Wiedemann–Franz law in the underdoped cuprate superconductor YBCO. Phys. Rev. B 93, 064513 (2016).
Daou, R. et al. Linear temperature dependence of resistivity and change in the Fermi surface at the pseudogap critical point of a high-Tc superconductor. Nat. Phys. 5, 31–34 (2009).
Axe, J. D. & Crawford, M. K. Structural instabilities in lanthanum cuprate superconductors. J. Low Temp. Phys. 95, 271–284 (1994).
Acknowledgements
We thank L. Balents, K. Behnia, R. M. Fernandes, I. Garate, J. H. Han, C. Hess, S. A. Kivelson, P. A. Lee, A. H. MacDonald, J. E. Moore, B. J. Ramshaw, L. Savary, O. Sushkov, A.-M. S. Tremblay, R. Valenti and C. M. Varma for fruitful discussions. L.T. acknowledges support from the Canadian Institute for Advanced Research (CIFAR) as a Fellow, and funding from the Natural Sciences and Engineering Research Council of Canada (NSERC; PIN 123817), the Fonds de recherche du Québec – Nature et Technologies (FRQNT), the Canada Foundation for Innovation (CFI) and a Canada Research Chair. This research was undertaken thanks in part to funding from the Canada First Research Excellence Fund. Part of this work was funded by the EPiQS Initiative of the Gordon and Betty Moore Foundation (Grant GBMF5306 to L.T.). J.-S.Z. was supported by a US National Science Foundation grant (MRSEC DMR-1720595).
Author information
Authors and Affiliations
Contributions
G.G., S.T., M.-E.B. and E.L. performed the thermal Hall conductivity measurements. A.G., A.A., F.L., M.D. and N.D.-L. prepared and characterized the samples. J.-S.Z. grew the Nd-LSCO single crystals. S.P., T.T. and H.T. grew the Eu-LSCO and La2CuO4 single crystals. G.G. and L.T. wrote the manuscript, in consultation with all of the authors. L.T. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature Physics thanks Liling Sun and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data
Extended Data Fig. 1 Current and field orientation for κxy and κzy measurements.
Sketch of the thermal Hall measurement setup for a) J // a // -x and b) J // c // z. The Cartesian coordinate system is defined in the same way for the two samples.
Extended Data Fig. 2 Longitudinal thermal conductivities κxx and κzz in La2CuO4.
Thermal conductivity versus temperature in a field of magnitude H = 15 T for La2CuO4 (p = 0), plotted as a) κnn vs T and b) κnn / T vs T, for heat current directions J // a (n = x; blue) and J // c (n = z; red). The longitudinal thermal conductivity of phonons at low temperature is nearly isotropic, with κxx / κzz = κa / κc ~ 0.8 at T = 25 K.
Extended Data Fig. 3 Longitudinal thermal conductivities κxx and κzz in Nd-LSCO.
Thermal conductivity κnn versus temperature in a field of magnitude H = 15 T, plotted as κnn / T vs T, for a) Nd-LSCO with p = 0.21 and b) Nd-LSCO with p = 0.24, for heat current directions J // a (n = x; blue) and J // c (n = z; red). In panels c) and d), the thermal conductivity of charge carriers is subtracted, using the Wiedemann-Franz law to estimate its magnitude (see ref. 3). The longitudinal thermal conductivity of phonons at low temperature is nearly isotropic, with κxx / κzz = κa / κc ~ 1.2 and 1.3 at T = 25 K, for p = 0.21 and p = 0.24, respectively.
Extended Data Fig. 4 Anisotropy of electrical Hall conductivity in Nd-LSCO.
Electrical Hall conductivity σny versus temperature in a field of magnitude H = 15 T, plotted as L0 σny vs T, for Nd-LSCO with p = 0.24, for heat current directions J // a (n = x; blue) and J // c (n = z; red). The data for σzy are multiplied by a factor 250. We use the approximate relation σzy = ρzy / (ρzz ρxx), with ρzz and ρxx data taken from ref. 35. The σxy data are taken from ref. 3.
Extended Data Fig. 5 Electronic thermal Hall conductivity in Nd-LSCO p = 0.24.
Estimate of the maximal c-axis thermal Hall conductivity from charge carriers in our sample of Nd-LSCO with p = 0.24, obtained by applying the Wiedemann-Franz law to the measured electrical Hall conductivity σzy, namely κzy / T ≤ L0 σzy, where σzy ≤ ρzy / (ρzz ρyy). a) Electrical resistivity for J // c, ρzz vs T (from ref. 35); b) electrical Hall resistivity for J // c and H // a, ρzy vs T ; c) maximal electrical Hall conductivity for J // c and H // a, defined as σzy = ρzy / (ρzz ρxx) (with ρxx data from ref. 35), plotted as L0 σzy (multiplied by 60) vs T ; d) comparison of the measured electrical (σzy) and thermal (κzy) Hall conductivities, plotted as L0 σzy (blue) and κzy / T (red; Fig. 1b) vs T.
Extended Data Fig. 6 Field dependence of κzz and κzy in La2CuO4 and Nd-LSCO.
Upper panels: thermal conductivity κzz measured at H = 0 T (purple), 10 T (green) and 15 T (red), plotted as κzz / T vs T, for a) La2CuO4, b) Nd-LSCO with p = 0.21 and c) Nd-LSCO with p = 0.24. Lower panels: thermal Hall conductivity κzy measured at H = 10 T (purple) and 15 T (red), plotted as κzy / (T H) vs T, for d) La2CuO4, e) Nd-LSCO with p = 0.21 and f) Nd-LSCO with p = 0.24. We see that κzy is approximately linear in H.
Extended Data Fig. 7 Structural transition in Nd-LSCO.
a) Structural phase diagram of Nd-LSCO as a function of doping. The black dots and black line mark the structural transition from the LTO1 phase to the LTT phase at low temperature, at TLTT, as measured by x-ray diffraction36. The squares mark TLTT in our samples with p = 0.21 (blue) and p = 0.24 (green), as detected by dilatometry measurements (see panel b). b) Change in sample length L as a function of temperature, plotted as its derivative dL / dT vs T, measured in our c-axis sample of Nd-LSCO with p = 0.21 (blue) and in a sample of Nd-LSCO cut from the same large single crystal as, and next to, our c-axis sample of Nd-LSCO with p = 0.24 (green). The dip in the curves marks the structural phase transition from the LTO1 phase above to the LTT phase below the transition temperature TLTT, where TLTT = 82 ± 5 K at p = 0.21 and TLTT = 45 ± 10 K at p = 0.24. The error bars on the two values of TLTT correspond to the full width of each corresponding dip. These data confirm that our two Nd-LSCO samples, with p = 0.21 and p = 0.24, have the same crystal structure. This shows that all the differences observed in their properties, in particular the dramatic difference in their thermal Hall conductivity κzy (Fig. 1), are not due to a difference in structural properties. Instead, these differences are linked with the onset of the pseudogap phase at p* = 0.23.
Source data
Source Data Fig. 1
Source data for Figure 1
Rights and permissions
About this article
Cite this article
Grissonnanche, G., Thériault, S., Gourgout, A. et al. Chiral phonons in the pseudogap phase of cuprates. Nat. Phys. 16, 1108–1111 (2020). https://doi.org/10.1038/s41567-020-0965-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0965-y
This article is cited by
-
Phonons bend to magnetic fields
Nature Physics (2024)
-
Phonon chirality from impurity scattering in the antiferromagnetic phase of Sr2IrO4
Nature Physics (2024)
-
Magnon thermal Hall effect via emergent SU(3) flux on the antiferromagnetic skyrmion lattice
Nature Communications (2024)
-
A criterion for strange metallicity in the Lorenz ratio
npj Quantum Materials (2023)
-
The phonon thermal Hall angle in black phosphorus
Nature Communications (2023)