Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Electron acceleration in laboratory-produced turbulent collisionless shocks

Nature Physics volume 16, pages 916–920 (2020)Cite this article

Subjects

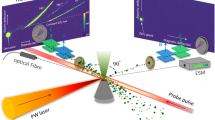
Abstract

Astrophysical collisionless shocks are among the most powerful particle accelerators in the Universe. Generated by violent interactions of supersonic plasma flows with the interstellar medium, supernova remnant shocks are observed to amplify magnetic fields1 and accelerate electrons and protons to highly relativistic speeds2,3,4. In the well-established model of diffusive shock acceleration5, relativistic particles are accelerated by repeated shock crossings. However, this requires a separate mechanism that pre-accelerates particles to enable shock crossing. This is known as the ‘injection problem’, which is particularly relevant for electrons, and remains one of the most important puzzles in shock acceleration6. In most astrophysical shocks, the details of the shock structure cannot be directly resolved, making it challenging to identify the injection mechanism. Here we report results from laser-driven plasma flow experiments, and related simulations, that probe the formation of turbulent collisionless shocks in conditions relevant to young supernova remnants. We show that electrons can be effectively accelerated in a first-order Fermi process by small-scale turbulence produced within the shock transition to relativistic non-thermal energies, helping overcome the injection problem. Our observations provide new insight into electron injection at shocks and open the way for controlled laboratory studies of the physics underlying cosmic accelerators.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Laser-driven collisionless shock experiments.
Fig. 2: Thomson scattering measurements indicating shock formation.
Fig. 3: Two-dimensional PIC simulation of the shock structure.
Fig. 4: Non-thermal electron acceleration.

Similar content being viewed by others

Data availability

The data represented in Fig. 2, Fig. 3c,d and Fig. 4 are provided with the paper as source data. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Code availability

The PIC code OSIRIS36,37 used in this study can be obtained from the OSIRIS Consortium, consisting of UCLA and IST (Portugal).

References

  1. Völk, H. J., Berezhko, E. G. & Ksenofontov, L. T. Magnetic field amplification in tycho and other shell-type supernova remnants. Astron. Astrophys. 433, 229–240 (2005).

    Article  ADS  Google Scholar 

  2. Koyama, K. et al. Evidence for shock acceleration of high-energy electrons in the supernova remnant SN1006. Nature 378, 255–258 (1995).

    Article  ADS  Google Scholar 

  3. Aharonian, F. A. et al. High-energy particle acceleration in the shell of a supernova remnant. Nature 432, 75–77 (2004).

    Article  ADS  Google Scholar 

  4. Ackermann, M. et al. Detection of the characteristic pion-decay signature in supernova remnants. Science 339, 807–811 (2013).

    Article  ADS  Google Scholar 

  5. Blandford, R. & Eichler, D. Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154, 1–75 (1987).

    Article  ADS  Google Scholar 

  6. Treumann, R. A. Fundamentals of collisionless shocks for astrophysical application, 1. non-relativistic shocks. Astron. Astrophys. Rev. 17, 409–535 (2009).

    Article  ADS  Google Scholar 

  7. Sagdeev, R. Z. Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23–91 (1966).

    ADS  Google Scholar 

  8. Oka, M. et al. Electron scattering by high-frequency whistler waves at Earth’s bow shock. Astrophys. J. 842, L11 (2017).

    Article  ADS  Google Scholar 

  9. Hoshino, M. & Shimada, N. Nonthermal electrons at high mach number shocks: electron shock surfing acceleration. Astrophys. J. 572, 880–887 (2002).

    Article  ADS  Google Scholar 

  10. Spitkovsky, A. Particle acceleration in relativistic collisionless shocks: Fermi process at last? Astrophys. J. 682, L5–L8 (2008).

    Article  ADS  Google Scholar 

  11. Kato, T. N. & Takabe, H. Nonrelativistic collisionless shocks in unmagnetized electron-ion plasmas. Astrophys. J. 681, L93–L96 (2008).

    Article  ADS  Google Scholar 

  12. Matsumoto, Y., Amano, T., Kato, T. N. & Hoshino, M. Stochastic electron acceleration during spontaneous turbulent reconnection in a strong shock wave. Science 347, 974–978 (2015).

    Article  ADS  Google Scholar 

  13. Kugland, N. L. et al. Self-organized electromagnetic field structures in laser-produced counter-streaming plasmas. Nat. Phys. 8, 809–812 (2012).

    Article  Google Scholar 

  14. Ross, J. S. et al. Characterizing counter-streaming interpenetrating plasmas relevant to astrophysical collisionless shocks. Phys. Plasmas 19, 056501 (2012).

    Article  ADS  Google Scholar 

  15. Fox, W. et al. Filamentation instability of counterstreaming laser-driven plasmas. Phys. Rev. Lett. 111, 225002 (2013).

    Article  ADS  Google Scholar 

  16. Huntington, C. M. et al. Observation of magnetic field generation via the Weibel instability in interpenetrating plasma flows. Nat. Phys. 11, 173–176 (2015).

    Article  Google Scholar 

  17. Ross, J. S. et al. Transition from collisional to collisionless regimes in interpenetrating plasma flows on the national ignition facility. Phys. Rev. Lett. 118, 185003 (2017).

    Article  ADS  Google Scholar 

  18. Schaeffer, D. B. et al. Generation and evolution of high-mach-number laser-driven magnetized collisionless shocks in the laboratory. Phys. Rev. Lett. 119, 025001 (2017).

    Article  ADS  Google Scholar 

  19. Li, C. K. et al. Collisionless shocks driven by supersonic plasma flows with self-generated magnetic fields. Phys. Rev. Lett. 123, 055002 (2019).

    Article  ADS  Google Scholar 

  20. Rigby, A. et al. Electron acceleration by wave turbulence in a magnetized plasma. Nat. Phys. 14, 1745–2481 (2018).

    Article  Google Scholar 

  21. Ryutov, D. D. et al. Basic scalings for collisionless-shock experiments in a plasma without pre-imposed magnetic field. Plasma Phys. Control. Fusion 54, 105021 (2012).

    Article  ADS  Google Scholar 

  22. Takabe, H. et al. High-mach number collisionless shock and photo-ionized non-LTE plasma for laboratory astrophysics with intense lasers. Plasma Phys. Control. Fusion 50, 124057 (2008).

    Article  ADS  Google Scholar 

  23. Tidman, D. A. & Krall, N. A. Shock Waves in Collisionless Plasmas (Wiley-Interscience, 1971).

  24. Gurevich, A. V. et al. Self-similar motion of rarefied plasma. Sov. Phys. J. Exp. Theor. Phys. 22, 449–454 (1966).

    ADS  Google Scholar 

  25. Trubnikov, B. A. Particle interactions in a fully ionized plasma. Rev. Plasma Phys. 1, 105 (1965).

    ADS  Google Scholar 

  26. Weibel, E. S. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 2, 83–84 (1959).

    Article  ADS  Google Scholar 

  27. Fried, B. D. Mechanism for instability of transverse plasma waves. Phys. Fluids 2, 337–337 (1959).

    Article  ADS  Google Scholar 

  28. Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O. & Mori, W. B. Long-time evolution of magnetic fields in relativistic gamma-ray burst shocks. Astrophys. J. 618, L75–L78 (2004).

    Article  ADS  Google Scholar 

  29. Ruyer, C. & Fiuza, F. Disruption of current filaments and isotropization of the magnetic field in counterstreaming plasmas. Phys. Rev. Lett. 120, 245002 (2018).

    Article  ADS  Google Scholar 

  30. Hillas, A. M. The origin of ultra-high-energy cosmic rays. Annu. Rev. Astron. Astrophys. 22, 425–444 (1984).

    Article  ADS  Google Scholar 

  31. Froula, D. H., Glenzer, S. H., Luhmann, N. C. & Sheffield, J. (eds) Plasma Scattering of Electromagnetic Radiation 2nd edn (Academic Press, 2011).

  32. Mariscal, D. et al. Calibration of proton dispersion for the NIF electron positron proton spectrometer (NEPPS) for short-pulse laser experiments on the NIF ARC. Rev. Sci. Instrum. 89, 10I145 (2018).

    Article  Google Scholar 

  33. Bonnet, T. et al. Response functions of imaging plates to photons, electrons and 4He particles. Rev. Sci. Instrum. 84, 103510 (2013).

    Article  ADS  Google Scholar 

  34. Halverson, W. Bremsstrahlung photon emission rate from Maxwellian plasmas. Plasma Phys. 14, 601–604 (1972).

    Article  ADS  Google Scholar 

  35. Marinak, M. M. et al. Three-dimensional hydra simulations of National Ignition Facility targets. Phys. Plasmas 8, 2275–2280 (2001).

    Article  ADS  Google Scholar 

  36. Fonseca, R. A et al. OSIRIS: A Three-Dimensional, Fully Relativistic Particle in Cell Code for Modeling Plasma Based Accelerators (Springer, 2002).

  37. Fonseca, R. A. et al. One-to-one direct modeling of experiments and astrophysical scenarios: pushing the envelope on kinetic plasma simulations. Plasma Phys. Control. Fusion 50, 124034 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank M. Hohenberger and G. Fiksel for their assistance in the analysis of FFLEX and NEPPS data, respectively. This work was supported by the US Department of Energy SLAC contract no. DE-AC02-76SF00515 and Lawrence Livermore National Laboratory contract no. DE-AC52-07NA27344, the US DOE Early Career Research Program under FWP 100331, the US DOE Office of Science, Fusion Energy Sciences under FWP 100182, the LLNL Laboratory Directed Research and Development Program grant 15-ERD-065, and the Engineering and Physical Sciences Research Council of the United Kingdom (grant nos. EP/M022331/1 and EP/N014472/1). We also acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Portugal) for the use of the OSIRIS 4.0 framework and the visXD framework. Simulations were run on Mira and Theta (ALCF) through ALCC awards and on Vulcan and Quartz (LLNL) through grand challenge awards.

Author information

Authors and Affiliations

  1. High Energy Density Science Division, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    F. Fiuza, A. Grassi, C. Bruulsema, S. Glenzer & W. Rozmus

  2. Lawrence Livermore National Laboratory, Livermore, CA, USA

    G. F. Swadling, D. P. Higginson, D. D. Ryutov, B. B. Pollock, B. A. Remington, J. S. Ross, S. Wilks & H.-S. Park

  3. Laboratory for Laser Energetics, University of Rochester, Rochester, NY, USA

    H. G. Rinderknecht

  4. Department of Physics, University of Alberta, Edmonton, Alberta, Canada

    C. Bruulsema & W. Rozmus

  5. University of Michigan, Ann Arbor, MI, USA

    R. P. Drake

  6. Friedrich-Alexander-Universitat Erlangen-Nuremberg, Erlangen Centre for Astroparticle Physics, Erlangen, Germany

    S. Funk

  7. Department of Physics, Oxford University, Oxford, UK

    G. Gregori

  8. Massachusetts Institute of Technology, Cambridge, MA, USA

    C. K. Li

  9. Osaka University, Osaka, Japan

    Y. Sakawa

  10. Princeton University, Princeton, NJ, USA

    A. Spitkovsky

Authors
  1. F. Fiuza
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. F. Swadling
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Grassi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. G. Rinderknecht
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. P. Higginson
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. D. D. Ryutov
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. C. Bruulsema
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. R. P. Drake
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. S. Funk
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. S. Glenzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. G. Gregori
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. C. K. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. B. B. Pollock
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. B. A. Remington
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. J. S. Ross
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. W. Rozmus
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Y. Sakawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. A. Spitkovsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. S. Wilks
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. H.-S. Park
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

F.F. and H.-S.P. conceived and led this project. The experiments were designed and carried out by G.F.S., H.G.R., H.-S.P. and F.F. The data were analysed by G.F.S., H.G.R., C.B., B.B.P. and F.F. Numerical simulations were performed by A.G., F.F., D.P.H. and S.W. Additional theoretical support was provided by D.D.R., W.R., A.S. and G.G. The paper was written by F.F. with contributions from all the authors.

Corresponding author

Correspondence to F. Fiuza.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

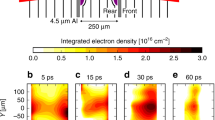
Extended Data Fig. 1 X-ray self emission from the plasma.

Lineouts of the X-ray signal along the mid-plane between the two targets for a) single flow and b) double flow experiments at 15 ns from the laser irradiation. The gated X-ray detector uses Vanadium (V, left) and Nickel (Ni, right) filters. The measured signal ratio between double flow and single flow experiments is ~100−200, consistent with predictions based on the plasma density and temperature from Thomson scattering measurements.

Supplementary information

Supplementary Information

Supplementary Figs. 1–4, discussion, and Tables 1 and 2.

Source data

Source Data Fig. 2

Numerical data used to generate the graphs in Fig. 2.

Source Data Fig. 3

Numerical data used to generate the graphs in Fig. 3c,d.

Source Data Fig. 4

Numerical data used to generate the graphs in the Fig. 4a,b,c(inset),4d.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fiuza, F., Swadling, G.F., Grassi, A. et al. Electron acceleration in laboratory-produced turbulent collisionless shocks. Nat. Phys. 16, 916–920 (2020). https://doi.org/10.1038/s41567-020-0919-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-020-0919-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing