Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Non-Hermitian linear response theory

Nature Physics volume 16, pages 767–771 (2020)Cite this article

Subjects

Abstract

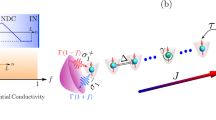
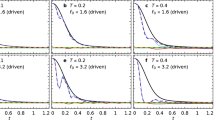
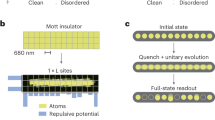
Linear response theory lies at the heart of studying quantum matters, because it connects the dynamical response of a quantum system to an external probe to correlation functions of the unprobed equilibrium state. Thanks to linear response theory, various experimental probes can be used for determining equilibrium properties. However, so far, both the unprobed system and the probe operator are limited to Hermitian ones. Here, we develop a non-Hermitian linear response theory that considers the dynamical response of a Hermitian system to a non-Hermitian probe, and we can also relate such a dynamical response to the properties of an unprobed Hermitian system at equilibrium. As an application of our theory, we consider the real-time dynamics of momentum distribution induced by one-body and two-body dissipations. Remarkably, for a critical state with no well-defined quasi-particles, we find that the dynamics are slower than the normal state with well-defined quasi-particles, and our theory provides a model-independent way to extract the critical exponent in the real-time correlation function. We find surprisingly good agreement between our theory and a recent cold atom experiment on the dissipative Bose–Hubbard model. We also propose to further quantitatively verify our theory by performing experiments on dissipative one-dimensional Luttinger liquid.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic of real-time dynamics of the momentum distribution induced by dissipations.
Fig. 2: Reanalysis, using our theory, of experimental data for the dissipative 2D Bose–Hubbard model reported in ref. 2.
Fig. 3: Experimental proposal of dissipative Luttinger liquids.

Similar content being viewed by others

Data availability

All the data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

References

  1. Mahan, G. D. Many Particle Physics (Plenum Press, 1981).

  2. Bouganne, R., Aguilera, M. B., Ghermaoui, A., Beugnon, J. & Gerbier, F. Anomalous decay of coherence in a dissipative many-body system. Nat. Phys. 16, 21–25 (2020).

    Article  Google Scholar 

  3. Syassen, N. et al. Strong dissipation inhibits losses and induces correlations in cold molecular gases. Science 320, 1329–1331 (2008).

    Article  ADS  Google Scholar 

  4. Barontini, G. et al. Controlling the dynamics of an open many-body quantum system with localized dissipation. Phys. Rev. Lett. 110, 035302 (2013).

    Article  ADS  Google Scholar 

  5. Tomita, T., Nakajima, S., Danshita, I., Takasu, Y. & Takahashi, Y. Observation of the Mott insulator to superfluid crossover of a driven-dissipative Bose–Hubbard system. Sci. Adv. 99, e1701513 (2017).

    Article  ADS  Google Scholar 

  6. Sponselee, K. et al. Dynamics of ultracold quantum gases in the dissipative Fermi–Hubbard model. Quantum Sci. Technol. 4, 014002 (2018).

    Article  ADS  Google Scholar 

  7. Li, J. et al. Observation of parity–time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun. 10, 855 (2019).

    Article  ADS  Google Scholar 

  8. Tomita, T., Nakajima, S., Takasu, Y. & Takahashi, Y. Dissipative Bose–Hubbard system with intrinsic two-body loss. Phys. Rev. A 99, 031601 (2019).

    Article  ADS  Google Scholar 

  9. Lee, T. E. Anomalous edge state in a non-Hermitian lattice. Phys. Rev. Lett. 116, 133903 (2016).

    Article  ADS  Google Scholar 

  10. Leykam, D., Bliokh, K. Y., Huang, C., Chong, Y. D. & Nori, F. Edge modes, degeneracies and topological numbers in non-Hermitian systems. Phys. Rev. Lett. 118, 040401 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  11. Shen, H., Zhen, B. & Fu, L. Topological band theory for non-Hermitian Hamiltonians. Phys. Rev. Lett. 120, 146402 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  12. Yao, S. & Wang, Z. Edge states and topological invariants of non-Hermitian systems. Phys. Rev. Lett. 121, 086803 (2018).

    Article  ADS  Google Scholar 

  13. Kunst, F. K., Edvardsson, E., Budich, J. C. & Bergholtz, E. J. Biorthogonal bulk-boundary correspondence in non-Hermitian systems. Phys. Rev. Lett. 121, 026808 (2018).

    Article  ADS  Google Scholar 

  14. Gong, Z. et al. Topological phases of non-Hermitian systems. Phys. Rev. X 8, 031079 (2018).

    Google Scholar 

  15. Chen, Y. & Zhai, H. Hall conductance of a non-Hermitian Chern insulator. Phys. Rev. B 98, 245130 (2018).

    Article  ADS  Google Scholar 

  16. Kawabata, K., Shiozaki, K., Ueda, M. & Sato, M. Symmetry and topology in non-Hermitian physics. Phys. Rev. X 9, 041015 (2019).

    Google Scholar 

  17. Lee, C. H. & Thomale, R. Anatomy of skin modes and topology in non-Hermitian systems. Phys. Rev. B 99, 201103 (2019).

    Article  ADS  Google Scholar 

  18. Lee, J. Y., Ahn, J., Zhou, H. & Vishwanath, A. Topological correspondence between Hermitian and non-Hermitian systems: anomalous dynamics. Phys. Rev. Lett. 123, 206404 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  19. Zeuner, J. M. et al. Observation of a topological transition in the bulk of a non-Hermitian system. Phys. Rev. Lett. 115, 040402 (2015).

    Article  ADS  Google Scholar 

  20. Zhou, H. et al. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science 359, 1009–1012 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  21. Harari, G. et al. Topological insulator laser: theory. Science 359, eaar4003 (2018).

    Article  Google Scholar 

  22. Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).

    Article  Google Scholar 

  23. Helbig, T. et al. Observation of bulk boundary correspondence breakdown in topolectrical circuits. Preprint at https://arxiv.org/abs/1907.11562 (2019).

  24. Xiao, L. Non-Hermitian bulk-boundary correspondence in quantum dynamics. Nat. Phys. (2020); https://doi.org/10.1038/s41567-020-0836-6

  25. Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999).

  26. Kamenev, A. Field Theory for Non-Equilibrium Systems (Cambridge Univ. Press, 2011).

  27. Pourfath, M.The Non-Equilibrium Green’s Function Method for Nanoscale Device Simulation (ed. Selberherr, S.) (Springer, 2014).

  28. Zinn-Justin, J. Phase Transitions and Renormalisation Group (Oxford Univ. Press, 2007).

  29. Witczak-Krempa, W., Sørensen, E. S. & Sachdev, S. The dynamics of quantum criticality revealed by quantum Monte Carlo and holography. Nat. Phys. 10, 361–366 (2014).

    Article  Google Scholar 

  30. Giamarchi, T. Quantum Physics in One Dimension (Oxford Science, 2004).

  31. Lieb, E. H. & Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 130, 1605–1616 (1963).

    Article  ADS  MathSciNet  Google Scholar 

  32. Imambekov, A. & Glazman, L. I. Exact exponents of edge singularities in dynamic correlation functions of 1D Bose gas. Phys. Rev. Lett. 100, 206805 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the Beijing Outstanding Young Scientist Program (H.Z.), NSFC grant no. 11734010 (H.Z. and Y.C.), NSFC grant no. 11604225 (Y.C.), MOST grant no. 2016YFA0301600 (H.Z.) and the Beijing Natural Science Foundation (Z180013; Y.C.).

Author information

Authors and Affiliations

  1. Institute for Advanced Study, Tsinghua University, Beijing, China

    Lei Pan, Xin Chen & Hui Zhai

  2. Graduate School of China Academy of Engineering Physics, Beijing, China

    Yu Chen

  3. Center for Theoretical Physics and Department of Physics, Capital Normal University, Beijing, China

    Yu Chen

Authors
  1. Lei Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xin Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hui Zhai
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

H.Z. initiated the project. H.Z. and Y.C. led the project. All authors contributed to performing calculations, discussing the results and writing the paper.

Corresponding authors

Correspondence to Yu Chen or Hui Zhai.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Discussion.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pan, L., Chen, X., Chen, Y. et al. Non-Hermitian linear response theory. Nat. Phys. 16, 767–771 (2020). https://doi.org/10.1038/s41567-020-0889-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-020-0889-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing