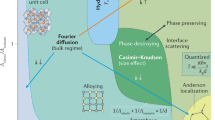
Abstract
In an insulator, thermal transport at high temperature is expected to be dominated by entirely classical phonon dynamics. In apparent tension with this expectation, recent experimental observations have led to the conjecture that the transport lifetime, τ, is subject to a Planckian bound from below, namely, τ ≳ τPl ≡ ℏ ∕ (kBT). Here, we argue that this Planckian bound is due to a quantum-mechanical bound on the sound velocity: vs < vM. The ‘melting velocity’ vM is defined in terms of the melting temperature of the crystal, the interatomic spacing and Planck’s constant. We show that for several classes of insulating crystals, both simple and complex, τ ∕ τPl ≈ vM ∕ vs at high temperatures. The velocity bound therefore implies the Planckian bound.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
References
Martelli, V., Jiménez, J. L., Continentino, M., Baggio-Saitovitch, E. & Behnia, K. Thermal transport and phonon hydrodynamics in strontium titanate. Phys. Rev. Lett. 120, 125901 (2018).
Behnia, K. & Kapitulnik, A. A lower bound to the thermal diffusivity of insulators. J. Phys. Condens. Matter 31, 405702 (2019).
Zhang, J., Kountz, E. D., Behnia, K. & Kapitulnik, A. Thermalization and possible signatures of quantum chaos in complex crystalline materials. Proc. Natl Acad. Sci. USA 116, 19869–19874 (2019).
Zaanen, J. Why the temperature is high. Nature 430, 512–513 (2004).
Hartnoll, S. A. Theory of universal incoherent metallic transport. Nat. Phys. 11, 54–61 (2014).
Peierls, R. On the statistical basis for the electron theory of metals. Helv. Phys. Act. (Supp.) 7, 24–30 (1934).
Peierls, R. Remarks on the theory of metals. Z. Phys. 88, 786–791 (1934).
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999).
Bruin, J. A. N., Sakai, H., Perry, R. S. & Mackenzie, A. P. Similarity of scattering rates in metals showing T-linear resistivity. Science 339, 804–807 (2013).
Zhang, J. et al. Anomalous thermal diffusivity in underdoped YBa2Cu3O6+x. Proc. Natl Acad. Sci. USA 114, 5378–5383 (2017).
Zhang, J. et al. Thermal diffusivity above the Mott-Ioffe-Regel limit. Phys. Rev. B 100, 241114 (2019).
Legros, A. et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat. Phys. 15, 142–147 (2019).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 142, 076801 (2019).
Feng, L., Shiga, T. & Shiomi, J. Phonon transport in perovskite SrTiO3 from first principles. Appl. Phys. Express 8, 071501 (2015).
Tadano, T. & Tsuneyuki, S. Self-consistent phonon calculations of lattice dynamical properties in cubic SrTiO3 with first-principles anharmonic force constants. Phys. Rev. B 92, 054301 (2015).
Slack, G. A. in Solid State Physics Vol. 34, 1–71 (Academic Press, 1979).
McGaughey, A. J. H., Jain, A., Kim, H.-Y. & Fu, B. Phonon properties and thermal conductivity from first principles, lattice dynamics, and the Boltzmann transport equation. J. Appl. Phys. 125, 011101 (2019).
Lindsay, L., Katre, A., Cepellotti, A. & Mingo, N. Perspective on ab initio phonon thermal transport. J. Appl. Phys. 126, 050902 (2019).
Grimvall, G. & Sjodin, S. Correlation of properties of materials to Debye and melting temperatures. Physica Scripta 10, 340–352 (1974).
Poirier, J. Lindemann law and the melting temperature of perovskites. Phys. Earth Planet. Inter. 54, 364–369 (1989).
Ziman, J. M. Electrons and Phonons: The Theory of Transport Phenomena in Solids (Oxford Univ. Press, 1960).
Auerbach, A. & Allen, P. B. Universal high-temperature saturation in phonon and electron transport. Phys. Rev. B 29, 2884–2890 (1984).
Kittel, C. Interpretation of the thermal conductivity of glasses. Phys. Rev. 75, 972–974 (1949).
Cahill, D. G., Watson, S. K. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131–6140 (1992).
Allen, P. B., Du, X., Mihaly, L. & Forro, L. Thermal conductivity of insulating Bi2Sr2YCu2O8 and superconducting Bi2Sr2CaCu2O8: failure of the phonon-gas picture. Phys. Rev. B 49, 9073–9079 (1994).
Feng, T., Lindsay, L. & Ruan, X. Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96, 161201 (2017).
Ladd, A. J. C., Moran, B. & Hoover, W. G. Lattice thermal conductivity: a comparison of molecular dynamics and anharmonic lattice dynamics. Phys. Rev. B 34, 5058–5064 (1986).
Glensk, A. et al. Phonon lifetimes throughout the Brillouin zone at elevated temperatures from experiment and ab initio. Phys. Rev. Lett. 123, 235501 (2019).
Sun, T. & Allen, P. B. Lattice thermal conductivity: computations and theory of the high-temperature breakdown of the phonon-gas model. Phys. Rev. B 82, 224305 (2010).
Lieb, E. H. & Robinson, D. W. The finite group velocity of quantum spin systems. Commun. Math. Phys. 28, 251–257 (1972).
Hartman, T., Hartnoll, S. A. & Mahajan, R. Upper bound on diffusivity. Phys. Rev. Lett. 119, 141601 (2017).
Nachtergaele, B., Raz, H., Schlein, B. & Sims, R. Lieb-Robinson bounds for harmonic and anharmonic lattice systems. Commun. Math. Phys. 286, 1073–1098 (2009).
Nussinov, Z. Infinite range correlations in non-equilibrium quantum systems and their possible experimental realizations. Nucl. Phys. B 953, 114948 (2017).
Zhang, D.-B., Allen, P. B., Sun, T. & Wentzcovitch, R. M. Thermal conductivity from phonon quasiparticles with subminimal mean free path in the MgSiO3 perovskite. Phys. Rev. B 96, 100302 (2017).
Tian, Z. et al. Phonon conduction in PbSe, PbTe, and PbTe1−xSex from first-principles calculations. Phys. Rev. B 85, 184303 (2012).
Martin, C. J. & O’Connor, D. A. An experimental test of Lindemann’s melting law. J. Phys. C Solid State Phys. 10, 3521–3526 (1977).
Yu, X. & Hofmeister, A. M. Thermal diffusivity of alkali and silver halide crystals as a function of temperature. J. Appl. Phys. 109, 033516 (2011).
Slack, G. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 34, 321–335 (1973).
Zeier, W. G. et al. Thinking like a chemist: intuition in thermoelectric materials. Angew. Chem. Int. Ed. 55, 6826–6841 (2016).
Lee, S. et al. Resonant bonding leads to low lattice thermal conductivity. Nat. Commun. 5, 3525 (2014).
Lindsay, L. & Broido, D. A. Three-phonon phase space and lattice thermal conductivity in semiconductors. J. Phys. Condens. Matter 20, 165209 (2008).
Ju, S. et al. Exploring diamond-like lattice thermal conductivity crystals via feature-based transfer learning. Preprint at https://arxiv.org/abs/1909.11234 (2019).
Wehinger, B. et al. Dynamical and elastic properties of MgSiO3 perovskite (bridgmanite). Geophys. Res. Lett. 43, 2568–2575 (2016).
Suda, J. et al. The first-order Raman spectra and lattice dynamics for YAlO3 crystal. J. Phys. Soc. Jpn 72, 1418–1422 (2003).
Acknowledgements
We thank K. Behnia, A. Kapitulnik, S. Kivelson and J. Zaanen for their insightful comments and criticism. We also thank Z. Han and D. Shi for discussions on related topics. This work is supported by the Department of Energy, Office of Basic Energy Sciences, under contract no. DEAC02-76SF00515. C.H.M. is supported by an NSF graduate fellowship.
Author information
Authors and Affiliations
Contributions
C.H.M. and S.A.H. both conceived and performed the research, and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary table and refs. 1–45.
Source data
Source Data Fig. 1
Labelled data points.
Source Data Fig. 2
Labelled data points.
Source Data Fig. 3
Labelled data points.
Rights and permissions
About this article
Cite this article
Mousatov, C.H., Hartnoll, S.A. On the Planckian bound for heat diffusion in insulators. Nat. Phys. 16, 579–584 (2020). https://doi.org/10.1038/s41567-020-0828-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0828-6
This article is cited by
-
How heat propagates in liquid 3He
Nature Communications (2024)
-
Phonons, electrons and thermal transport in Planckian high Tc materials
npj Quantum Materials (2021)
-
On the universality of AdS2 diffusion bounds and the breakdown of linearized hydrodynamics
Journal of High Energy Physics (2021)
-
Holographic axion model: A simple gravitational tool for quantum matter
Science China Physics, Mechanics & Astronomy (2021)