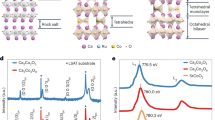
Abstract
In the context of correlated insulators, where electron–electron interactions (U) drive the localization of charge carriers, the metal–insulator transition is described as either bandwidth- or filling-controlled1. Motivated by the challenge of the insulating phase in Sr2IrO4, a new class of correlated insulators has been proposed, in which spin–orbit coupling (SOC) is believed to renormalize the bandwidth of the half-filled jeff = 1/2 doublet, allowing a modest U to induce a charge-localized phase2,3. Although this framework has been tacitly assumed, a thorough characterization of the ground state has been elusive4,5. Furthermore, direct evidence for the role of SOC in stabilizing the insulating state has not been established, because previous attempts at revealing the role of SOC6,7 have been hindered by concurrently occurring changes to the filling8,9,10. We overcome this challenge by employing multiple substituents that introduce well-defined changes to the signatures of SOC and carrier concentration in the electronic structure, as well as a new methodology that allows us to monitor SOC directly. Specifically, we study Sr2Ir1−xTxO4 (T = Ru, Rh) by angle-resolved photoemission spectroscopy, combined with ab initio and supercell tight-binding calculations. This allows us to distinguish relativistic and filling effects, thereby establishing conclusively the central role of SOC in stabilizing the insulating state of Sr2IrO4. Most importantly, we estimate the critical value for SOC in this system to be λc = 0.42 ± 0.01 eV, and provide the first demonstration of a spin–orbit-controlled metal–insulator transition.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Imada, M., Fujimori, A. & Tokura, Y. Metal–insulator transitions. Rev. Mod. Phys. 70, 1039 (1998).
Kim, B. J. et al. Novel J eff=1/2 Mott state induced by relativistic spin–orbit coupling in Sr2IrO4. Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin–orbital Mott state in Sr2IrO4. Science 323, 1329–1332 (2009).
MorettiSala, M., Boseggia, S., McMorrow, D. F. & Monaco, G. Resonant X-ray scattering and the j eff=1/2 electronic ground state in iridate perovskites. Phys. Rev. Lett. 112, 026403 (2014).
Kim, B. J. & Khaliullin, G. Resonant inelastic X-ray scattering operators for t 2g orbital systems. Phys. Rev. B 96, 085108 (2017).
Qi, T. F. et al. Spin–orbit tuned metal–insulator transitions in single-crystal Sr2Ir1−xRhxO4 (0 ≤ x ≤ 1). Phys. Rev. B 86, 125105 (2012).
Lee, J. S., Krockenberger, Y., Takahashi, K. S., Kawasaki, M. & Tokura, Y. Insulator–metal transition driven by change of doping and spin–orbit interaction in Sr2IrO4. Phys. Rev. B 85, 035101 (2012).
Brouet, V. et al. Transfer of spectral weight across the gap of Sr2IrO4ind induced by La doping. Phys. Rev. B 92, 081117 (2015).
Cao, Y. et al. Hallmarks of the Mott-metal crossover in the hole-doped pseudospin-1/2 Mott insulator Sr2IrO4. Nat. Commun. 7, 11367 (2016).
Louat, A. et al. Formation of an incoherent metallic state in Rh-doped Sr2IrO4. Phys. Rev. B 97, 161109 (2018).
Mattheiss, L. F. Electronic structure of RuO2, OsO2 and IrO2. Phys. Rev. B 13, 2433–2450 (1976).
Moon, S. J. et al. Dimensionality-controlled insulator–metal transition and correlated metallic state in 5 d transition metal oxides Srn + 1IrnO3n + 1 (n = 1, 2 and ∞). Phys. Rev. Lett. 101, 226402 (2008).
Kim, B. H., Khaliullin, G. & Min, B. I. Magnetic couplings, optical spectra and spin–orbit exciton in 5d electron Mott insulator Sr2IrO4. Phys. Rev. Lett. 109, 167205 (2012).
Haverkort, M. W., Elfimov, I. S., Tjeng, L. H., Sawatzky, G. A. & Damascelli, A. Strong spin–orbit coupling effects on the Fermi surface of Sr2RuO4 and Sr2RhO4. Phys. Rev. Lett. 101, 026406 (2008).
Veenstra, C. N. et al. Spin–orbital entanglement and the breakdown of singlets and triplets in Sr2RuO4 revealed by spin- and angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 112, 127002 (2014).
Earnshaw, A., Figgis, B. N., Lewis, J. & Peacock, R. D. The magnetic properties of some d 4-complexes. J. Chem. Soc. 0, 3132 (1961).
Mravlje, J. et al. Coherence–incoherence crossover and the mass-renormalization puzzles in Sr2RuO4. Phys. Rev. Lett. 106, 096401 (2011).
Martins, C., Aichhorn, M., Vaugier, L. & Biermann, S. Reduced effective spin–orbital degeneracy and spin–orbital ordering in paramagnetic transition-metal oxides: Sr2IrO4 versus Sr2RhO4. Phys. Rev. Lett. 107, 266404 (2011).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Cava, R. J. et al. Localized-to-itinerant electron transition in Sr2Ir1 − xRuxO4. Phys. Rev. B 49, 11890 (1994).
Yuan, S. J. et al. From J eff=1/2 insulator to J eff=1/2 -wave superconductor in single-crystal J eff=1/2. Phys. Rev. B 92, 245103 (2015).
Wang, Z. et al. Disorder induced power-law gaps in an insulator–metal Mott transition. Proc. Natl Acad. Sci. USA 115, 11198 (2018).
Martins, C. Interplay of Spin–Orbit Coupling and Electronic Coulomb Interactions in Strontium Iridate Sr 2IrO 4. Thesis, Ecole Polytechnique X (2010).
Heidarian, D. & Trivedi, N. Inhomogeneous metallic phase in a disordered Mott insulator in two dimensions. Phys. Rev. Lett. 93, 126401 (2004).
Kaminski, A. et al. Renormalization of spectral line shape and dispersion below T c in Bi2Sr2CaCu2O8 + δ. Phys. Rev. Lett. 86, 1070–1073 (2001).
Damascelli, A. Probing the electronic structure of complex systems by ARPES. Phys. Scr. T109, 61 (2004).
Hufner, S. Photoelectron Spectroscopy: Principles and Applications (Springer, 1995).
Mahan, G. D. in Electron and Ion Spectroscopy of Solids (ed. Fiermans, L.) Ch. 1, 1–53 (Plenum Press, 1978).
Weeks, C., Hu, J., Alicea, J., Franz, M. & Wu, R. Engineering a robust quantum spin Hall state in graphene via adatom deposition. Phys. Rev. X 1, 021001 (2011).
Hu, J., Alicea, J., Wu, R. & Franz, M. Giant topological insulator gap in graphene with 5d adatoms. Phys. Rev. Lett. 109, 266801 (2012).
Carter, S. A. et al. Mechanism for the metal–insulator transition in Sr2Ir1−xRuxO4. Phys. Rev. B 51, 17184–17187 (1995).
Glamazda, A. et al. Effects of hole doping on magnetic and lattice excitations in Sr2Ir1−xRuxO4 (x = 0–0.2). Phys. Rev. B 89, 104406 (2014).
Calder, S. et al. Strong anisotropy within a Heisenberg model in the J eff=1/2 insulating state of Sr2Ir0.8Ru0.2O4. Phys. Rev. B 94, 220407 (2016).
Wadati, H., Elfimov, I. & Sawatzky, G. A. Where are the extra d electrons in transition-metal-substituted iron pnictides? Phys. Rev. Lett. 105, 157004 (2010).
Levy, G. et al. Probing the role of Co substitution in the electronic structure of iron pnictides. Phys. Rev. Lett. 109, 077001 (2012).
Boykin, T. B. & Klimeck, G. Practical application of zone-folding concepts in tight-binding calculations. Phys. Rev. B 71, 115215 (2005).
Ku, W., Berlijn, T. & Lee, C. C. Unfolding first-principles band structures. Phys. Rev. Lett. 104, 216401 (2010).
Haverkort, M. W., Elfimov, I. S. & Sawatzky, G. A. Electronic structure and self energies of randomly substituted solids using density functional theory and model calculations. Preprint at https://arxiv.org/abs/1109.4036 (2011).
Popescu, V. & Zunger, A. Extracting E versus \(\vec k\)E effective band structure from supercell calculations on alloys and impurities. Phys. Rev. B 85, 085201 (2012).
Watanabe, H., Shirakawa, T. & Yunoki, S. Microscopic study of a spin–orbit-induced Mott insulator in Ir oxides. Phys. Rev. Lett. 105, 216410 (2010).
Fluegel, B. et al. Giant spin–orbit bowing in GaAs1-xBix. Phys. Rev. Lett. 97, 067205 (2006).
Xu, S.-Y. et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 332, 560–564 (2011).
Sato, T. et al. Unexpected mass acquisition of dirac fermions at the quantum phase transition of a topological insulator. Nat. Phys 7, 840 (2011).
Brahlek, M. et al. Topological-metal to band-insulator transition in (Bi1-xInx)2Se3 thin films. Phys. Rev. Lett. 109, 186403 (2012).
Wu, L. et al. A sudden collapse in the transport lifetime across the topological phase transition in (Bi1-xInx)2Se3. Nat. Phys. 9, 410 (2013).
Vobornik, I. et al. Observation of distinct bulk and surface chemical environments in a topological insulator under magnetic doping. J. Phys. Chem. C 118, 12333–12339 (2014).
Avsar, A. et al. Spin–orbit proximity effect in graphene. Nat. Commun. 5, 4875 (2014).
Straßer, C. et al. Long- versus short-range scattering in doped epitaxial graphene. Nano Lett. 15, 2825–2829 (2015).
Barker, B. A. et al. Geometry and electronic structure of iridium adsorbed on graphene. Phys. Rev. B 99, 075431 (2019).
Mostofi, A. A. et al. An updated version of Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Blaha, P. et al. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universität Wien, 2018).
Kuneš, J. et al. Wien2wannier: from linearized augmented plane waves to maximally localized Wannier functions. Comput. Phys. Commun. 181, 1888–1895 (2010).
Day, R. P., Zwartsenberg, B., Elfimov, I. S. & Damascelli, A. Computational framework chinook for angle-resolved photoemission spectroscopy. Npj Quantum Mater. 4, 54 (2019).
Acknowledgements
We thank A. Nocera, M. Franz and G.A. Sawatzky for critical reading of the manuscript and useful discussions. This research was undertaken thanks in part to funding from the Max Planck-UBC-UTokyo Centre for Quantum Materials and the Canada First Research Excellence Fund, Quantum Materials and Future Technologies Program. The work at UBC was supported by the Killam, Alfred P. Sloan and Natural Sciences and Engineering Research Council of Canada’s (NSERC’s) Steacie Memorial Fellowships (A.D.), the Alexander von Humboldt Fellowship (A.D.), the Canada Research Chairs Program (A.D.), NSERC, Canada Foundation for Innovation (CFI) and the CIFAR Quantum Materials Program. E.R. acknowledges support from the Swiss National Science Foundation (SNSF, grant no. P300P2_164649). B.J.K. was supported by IBS - R014-A2.
Author information
Authors and Affiliations
Contributions
B.Z. and A.D. conceived the experiment. B.Z., E.R. and M.M. collected the experimental data. N.X., M.S. and J.D.D. provided experimental support. G.C., S.C., K.U., J.B., H.T. and B.J.K. grew the single crystals. B.Z. and R.P.D. performed data analysis. B.Z. performed simulations, with input from R.P.D., I.S.E. and A.D. B.Z., R.P.D. and A.D. wrote the manuscript, with input from all authors. I.S.E. and A.D. supervised the project. A.D. was responsible for overall project direction, planning and management.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer Review Information Nature Physics thanks Fahad Mahmood and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–4, discussion and references.
Source data
Source Data Fig. 2
Source data for Fig. 2 panels.
Source Data Fig. 3
Source data for Fig. 3 panels.
Rights and permissions
About this article
Cite this article
Zwartsenberg, B., Day, R.P., Razzoli, E. et al. Spin-orbit-controlled metal–insulator transition in Sr2IrO4. Nat. Phys. 16, 290–294 (2020). https://doi.org/10.1038/s41567-019-0750-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0750-y
This article is cited by
-
Coherent propagation of spin-orbit excitons in a correlated metal
npj Quantum Materials (2023)
-
Large-gap insulating dimer ground state in monolayer IrTe2
Nature Communications (2022)
-
Effects of the on-site energy on the electronic response of Sr3(Ir1−xMnx)2O7
Scientific Reports (2022)
-
Chemical bonding and Born charge in 1T-HfS2
npj 2D Materials and Applications (2021)
-
Quantum criticality in a layered iridate
Communications Physics (2021)