Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Accessing scrambling using matrix product operators

Nature Physics volume 16, pages 199–204 (2020)Cite this article

Subjects

Abstract

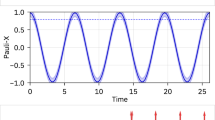
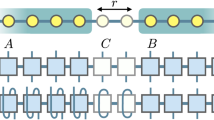
Scrambling, a process in which quantum information spreads over a complex quantum system, becoming inaccessible to simple probes, occurs in generic chaotic quantum many-body systems, ranging from spin chains to metals and even to black holes. Scrambling can be measured using out-of-time-ordered correlators (OTOCs), which are closely tied to the growth of Heisenberg operators. We present a general method to calculate OTOCs of local operators in one-dimensional systems based on approximating Heisenberg operators as matrix product operators (MPOs). Contrary to the common belief that such tensor network methods work only at early times, we show that the entire early growth region of the OTOC can be captured using an MPO approximation with modest bond dimension. We analytically establish the goodness of the approximation by showing that, if an appropriate OTOC is close to its initial value, then the associated Heisenberg operator has low entanglement across a given cut. We use the method to study scrambling in a chaotic spin chain with \(201\) sites. On the basis of these data and previous results, we conjecture a universal form for the dynamics of the OTOC near the wavefront. We show that this form collapses the chaotic spin chain data over more than 15 orders of magnitude.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Sketch of the emergent light cone and entanglement structure of local Heisenberg operators in tensor network forms.
Fig. 2: The operator entanglement entropy for the mixed-field Ising model.
Fig. 3: The early growth regime of the squared commutator for the mixed-field Ising model from MPO dynamics.
Fig. 4: The late-time regime of the squared commutator from the MPO dynamics with time splitting.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.

Code availability

The code used to perform the numerical simulation within this paper is available from the corresponding author on reasonable request.

References

  1. Hayden, P. & Preskill, J. Black holes as mirrors: quantum information in random subsystems. J. High Energy Phys. 2007, 120 (2007).

    MathSciNet  Google Scholar 

  2. Sekino, Y. & Susskind, L. Fast scramblers. J. High Energy Phys. 2008, 065 (2008).

    Google Scholar 

  3. Shenker, S. H. & Stanford, D. Black holes and the butterfly effect. J. High Energy Phys. 2014, 67 (2014).

    MathSciNet  MATH  Google Scholar 

  4. Hosur, P., Qi, X.-L., Roberts, D. A. & Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 4 (2016).

    MathSciNet  MATH  Google Scholar 

  5. Deutsch, J. M. Quantum statistical mechanics in a closed system. Phys. Rev. A 43, 2046–2049 (1991).

    ADS  Google Scholar 

  6. Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 50, 888–901 (1994).

    ADS  Google Scholar 

  7. Tasaki, H. From quantum dynamics to the canonical distribution: general picture and a rigorous example. Phys. Rev. Lett. 80, 1373–1376 (1998).

    ADS  MathSciNet  MATH  Google Scholar 

  8. Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854–858 (2008).

    ADS  Google Scholar 

  9. Sachdev, S. & Ye, J. Gapless spin-fluid ground state in a random quantum Heisenberg magnet. Phys. Rev. Lett. 70, 3339–3342 (1993).

    ADS  Google Scholar 

  10. Kitaev, A. A simple model of quantum holography. In KITP Program: Entanglement in Strongly-Correlated Quantum Matter http://online.kitp.ucsb.edu/online/entangled15/kitaev/ (2015).

  11. Gu, Y., Qi, X.-L. & Stanford, D. Local criticality, diffusion and chaos in generalized Sachdev–Ye–Kitaev models. J. High Energy Phys. 2017, 125 (2017).

    MathSciNet  MATH  Google Scholar 

  12. Maldacena, J., Shenker, S. H. & Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 106 (2016).

    MathSciNet  MATH  Google Scholar 

  13. Swingle, B. & Chowdhury, D. Slow scrambling in disordered quantum systems. Phys. Rev. B 95, 060201 (2017).

    ADS  Google Scholar 

  14. Chen, Y. Universal logarithmic scrambling in many body localization. Preprint at https://arxiv.org/abs/1608.02765 (2016).

  15. Fan, R., Zhang, P., Shen, H. & Zhai, H. Out-of-time-order correlation for many-body localization. Sci. Bull. 62, 707–711 (2017).

    Google Scholar 

  16. Huang, Y., Zhang, Y.-L. & Chen, X. Out-of-time-ordered correlators in many-body localized systems. Ann. Phys. 529, 1600318 (2017).

    Google Scholar 

  17. Swingle, B., Bentsen, G., Schleier-Smith, M. & Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 94, 040302 (2016).

    ADS  MathSciNet  Google Scholar 

  18. Zhu, G., Hafezi, M. & Grover, T. Measurement of many-body chaos using a quantum clock. Phys. Rev. A 94, 062329 (2016).

    ADS  Google Scholar 

  19. Yao, N.Y. et al. Interferometric approach to probing fast scrambling. Preprint at https://arxiv.org/abs/1607.01801 (2016).

  20. Yunger Halpern, N. Jarzynski-like equality for the out-of-time-ordered correlator. Phys. Rev. A 95, 012120 (2017).

    ADS  Google Scholar 

  21. Yunger Halpern, N., Swingle, B. & Dressel, J. Quasiprobability behind the out-of-time-ordered correlator. Phys. Rev. A 97, 042105 (2018).

    ADS  Google Scholar 

  22. Campisi, M. & Goold, J. Thermodynamics of quantum information scrambling. Phys. Rev. E 95, 062127 (2017).

    ADS  Google Scholar 

  23. Yoshida, B. & Kitaev, A. Efficient decoding for the Hayden-Preskill protocol. Preprint at https://arxiv.org/abs/1710.03363 (2017).

  24. Garttner, M. et al. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 13, 781–786 (2017).

    Google Scholar 

  25. Wei, K. X., Ramanathan, C. & Cappellaro, P. Exploring localization in nuclear spin chains. Phys. Rev. Lett. 120, 070501 (2018).

    ADS  Google Scholar 

  26. Li, J. et al. Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator. Phys. Rev. X 7, 031011 (2017).

    Google Scholar 

  27. Meier, E. J., Ang’ong’a, J., An, F. A. & Gadway, B. Exploring quantum signatures of chaos on a Floquet synthetic lattice. Phys. Rev. A 100, 013623 (2019).

    ADS  Google Scholar 

  28. Leviatan, E., Pollmann, F., Bardarson, J. H., Huse, D. A. & Altman, E. Quantum thermalization dynamics with matrix-product states. Preprint at https://arxiv.org/abs/1702.08894 (2017).

  29. Chen, X., Zhou, T. & Xu, C. Measuring the distance between quantum many-body wave functions. J. Stat. Mech. Theory Exp. 2018, 073101 (2018).

    MathSciNet  Google Scholar 

  30. Bordia, P., Alet, F. & Hosur, P. Out-of-time-ordered measurements as a probe of quantum dynamics. Phys. Rev. A 97, 030103 (2018).

    ADS  Google Scholar 

  31. Roberts, D. A. & Stanford, D. Diagnosing chaos using four-point functions in two-dimensional conformal field theory. Phys. Rev. Lett. 115, 131603 (2015).

    ADS  Google Scholar 

  32. Stanford, D. Many-body chaos at weak coupling. J. High Energy Phys. 2016, 9 (2016).

    MathSciNet  MATH  Google Scholar 

  33. Chowdhury, D. & Swingle, B. Onset of many-body chaos in the \(O(N)\) model. Phys. Rev. D 96, 065005 (2017).

    ADS  MathSciNet  Google Scholar 

  34. Patel, A. A., Chowdhury, D., Sachdev, S. & Swingle, B. Quantum butterfly effect in weakly interacting diffusive metals. Phys. Rev. X 7, 031047 (2017).

    Google Scholar 

  35. Nahum, A., Ruhman, J. & Huse, D. A. Dynamics of entanglement and transport in one-dimensional systems with quenched randomness. Phys. Rev. B 98, 035118 (2018).

    ADS  Google Scholar 

  36. Nahum, A., Vijay, S. & Haah, J. Operator spreading in random unitary circuits. Phys. Rev. X 8, 021014 (2018).

    Google Scholar 

  37. Khemani, V., Vishwanath, A. & Huse, D. A. Operator spreading and the emergence of dissipative hydrodynamics under unitary evolution with conservation laws. Phys. Rev. X 8, 031057 (2018).

    Google Scholar 

  38. Rakovszky, T., Pollmann, F. & vonKeyserlingk, C. W. Diffusive hydrodynamics of out-of-time-ordered correlators with charge conservation. Phys. Rev. X 8, 031058 (2018).

    Google Scholar 

  39. Luitz, D. J. & BarLev, Y. Information propagation in isolated quantum systems. Phys. Rev. B 96, 020406 (2017).

    ADS  Google Scholar 

  40. Bohrdt, A., Mendl, C. B., Endres, M. & Knap, M. Scrambling and thermalization in a diffusive quantum many-body system. New J. Phys. 19, 063001 (2016).

    Google Scholar 

  41. Heyl, M., Pollmann, F. & Dóra, B. Detecting equilibrium and dynamical quantum phase transitions in Ising chains via out-of-time-ordered correlators. Phys. Rev. Lett. 121, 016801 (2018).

    ADS  Google Scholar 

  42. Lin, C.-J. & Motrunich, O. I. Out-of-time-ordered correlators in a quantum Ising chain. Phys. Rev. B 97, 144304 (2018).

    ADS  Google Scholar 

  43. Vidal, G. Classical simulation of infinite-size quantum lattice systems in one spatial dimension. Phys. Rev. Lett. 98, 70201 (2007).

    ADS  Google Scholar 

  44. White, C. D., Zaletel, M., Mong, R. S. K. & Refael, G. Quantum dynamics of thermalizing systems. Phys. Rev. B 97, 035127 (2018).

    ADS  Google Scholar 

  45. Song, X. Y., Jian, C. M. & Balents, L. Strongly correlated metal built from Sachdev–Ye–Kitaev models. Phys. Rev. Lett. 119, 216601 (2017).

    ADS  Google Scholar 

  46. Ben-Zion, D. & McGreevy, J. Strange metal from local quantum chaos. Phys. Rev. B 97, 155117 (2018).

    ADS  Google Scholar 

  47. Lieb, E. H. & Robinson, D. W. The finite group velocity of quantum spin systems. Commun. Math. Phys. 28, 251–257 (1972).

    ADS  MathSciNet  Google Scholar 

  48. Nachtergaele, B. & Sims, R. Lieb–Robinson bounds in quantum many-body physics. In Entropy and the Quantum (eds R. Sims & D. Ueltschi) Contemporary Mathematics Vol. 529, 141–176 (American Mathematical Society, 2010).

  49. Gopalakrishnan, S., Huse, D. A., Khemani, V. & Vasseur, R. Hydrodynamics of operator spreading and quasiparticle diffusion in interacting integrable systems. Phys. Rev. B 98, 220303 (2018).

    ADS  Google Scholar 

Download references

Acknowledgements

We thank J. Garrison, D. Roberts, A. Kitaev and D. Stanford for interesting discussions. This material is based on work supported by the Simons Foundation via the It from Qubit Collaboration, by the Air Force Office of Scientific Research under award number FA9550-17-1-0180 and by the NSF Physics Frontier Center at the Joint Quantum Institute (PHY-1430094).

Author information

Authors and Affiliations

  1. Condensed Matter Theory Center and Department of Physics, University of Maryland, College Park, MD, USA

    Shenglong Xu & Brian Swingle

  2. Maryland Center for Fundamental Physics, Joint Center for Quantum Information and Computer Science, University of Maryland, College Park, MD, USA

    Brian Swingle

Authors
  1. Shenglong Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brian Swingle
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.X. and B.S. initiated the study. S.X. developed the computational tool and performed the numerical simulations. S.X. and B.S. analysed the results and wrote the manuscript.

Corresponding author

Correspondence to Brian Swingle.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Physics thanks Beni Yoshida and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Xu, S., Swingle, B. Accessing scrambling using matrix product operators. Nat. Phys. 16, 199–204 (2020). https://doi.org/10.1038/s41567-019-0712-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0712-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing