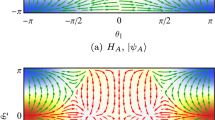
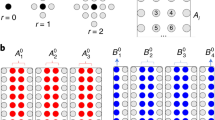
Abstract
The accurate computation of Hamiltonian ground, excited and thermal states on quantum computers stands to impact many problems in the physical and computer sciences, from quantum simulation to machine learning. Given the challenges posed in constructing large-scale quantum computers, these tasks should be carried out in a resource-efficient way. In this regard, existing techniques based on phase estimation or variational algorithms display potential disadvantages; phase estimation requires deep circuits with ancillae, that are hard to execute reliably without error correction, while variational algorithms, while flexible with respect to circuit depth, entail additional high-dimensional classical optimization. Here, we introduce the quantum imaginary time evolution and quantum Lanczos algorithms, which are analogues of classical algorithms for finding ground and excited states. Compared with their classical counterparts, they require exponentially less space and time per iteration, and can be implemented without deep circuits and ancillae, or high-dimensional optimization. We furthermore discuss quantum imaginary time evolution as a subroutine to generate Gibbs averages through an analogue of minimally entangled typical thermal states. Finally, we demonstrate the potential of these algorithms via an implementation using exact classical emulation as well as through prototype circuits on the Rigetti quantum virtual machine and Aspen-1 quantum processing unit.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request
Code availability
The code used to generate the data presented in this study can be publicly accessed on GitHub at https://github.com/mariomotta/QITE.git
Change history
29 January 2020
A Correction to this paper has been published: https://doi.org/10.1038/s41567-020-0798-8
21 November 2019
A Correction to this paper has been published: https://doi.org/10.1038/s41567-019-0756-5
References
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Abrams, D. S. & Lloyd, S. Simulation of many-body Fermi systems on a universal quantum computer. Phys. Rev. Lett. 79, 2586–2589 (1997).
Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Kempe, J., Kitaev, A. & Regev, O. The complexity of the local Hamiltonian problem. SIAM J. Comput. 35, 1070–1097 (2006).
Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. Quantum Computation by Adiabatic Evolution Report No. MIT-CTP-2936 (MIT, 2000).
Kitaev, A. Y. Quantum measurements and the Abelian stabilizer problem. Preprint at https://arxiv.org/abs/quant-ph/9511026 (1995).
Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. A quantum approximate optimization algorithm. Report No. MIT-CTP/4610 (MIT, 2014).
Otterbach, J. S. et al. Unsupervised machine learning on a hybrid quantum computer. Preprint at https://arxiv.org/abs/1712.05771 (2017).
Moll, N. et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 3, 030503 (2018).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2016).
Grimsley, H. R., Economou, S. E., Barnes, E. & Mayhall, N. J. An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 10, 3007 (2019).
McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 4812 (2018).
McArdle, S. et al. Variational ansatz-based quantum simulation of imaginary time evolution. npj Quantum Inf. 5, 75 (2019).
Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl Bur. Stand. B 45, 255–282 (1950).
Uhlmann, A. The ‘transition probability’ in the state space of a *-algebra. Rep. Math. Phys. 9, 273–279 (1976).
Hastings, M. B. & Koma, T. Spectral gap and exponential decay of correlations. Commun. Math. Phys. 265, 781–804 (2006).
Bravyi, S. B. & Kitaev, A. Y. Fermionic quantum computation. Ann. Phys. (N. Y.) 298, 210–226 (2002).
Verstraete, F. & Cirac, J. I. Mapping local Hamiltonians of fermions to local Hamiltonians of spins. J. Stat. Mech. 2005, P09012 (2005).
Berry, D. W., Childs, A. M. & Kothari, R. Hamiltonian simulation with nearly optimal dependence on all parameters. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science 792–809 (IEEE, 2015).
Vidal, G. Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. (N. Y.) 326, 96–192 (2011).
Schuch, N., Wolf, M. M., Verstraete, F. & Cirac, J. I. Computational complexity of projected entangled pair states. Phys. Rev. Lett. 98, 140506 (2007).
Haferkamp, J., Hangleiter, D., Eisert, J. & Gluza, M. Contracting projected entangled pair states is average-case hard. Preprint at https://arxiv.org/abs/1810.00738 (2018).
O’Malley, P. J. J. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007 (2016).
Lamm, H. & Lawrence, S. Simulation of nonequilibrium dynamics on a quantum computer. Phys. Rev. Lett. 121, 170501 (2018).
Rigetti Computing: Quantum Cloud Services; https://qcs.rigetti.com/dashboard
McClean, J. R., Kimchi-Schwartz, M. E., Carter, J. & de Jong, W. A. Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states. Phys. Rev. A 95, 042308 (2017).
Colless, J. I. et al. Computation of molecular spectra on a quantum processor with an error-resilient algorithm. Phys. Rev. X 8, 011021 (2018).
Terhal, B. M. & DiVincenzo, D. P. Problem of equilibration and the computation of correlation functions on a quantum computer. Phys. Rev. A 61, 022301 (2000).
Temme, K., Osborne, T. J., Vollbrecht, K. G., Poulin, D. & Verstraete, F. Quantum Metropolis sampling. Nature 471, 87 (2011).
Chowdhury, A. N. & Somma, R. D. Quantum algorithms for Gibbs sampling and hitting-time estimation. Quantum Inf. Comput. 17, 41–64 (2017).
Brandão, F. G. & Kastoryano, M. J. Finite correlation length implies efficient preparation of quantum thermal states. Commun. Math. Phys. 365, 1–16 (2019).
White, S. R. Minimally entangled typical quantum states at finite temperature. Phys. Rev. Lett. 102, 190601 (2009).
Stoudenmire, E. M. & White, S. R. Minimally entangled typical thermal state algorithms. New J. Phys. 12, 055026 (2010).
Acknowledgements
M.M., G.K.-L.C., F.G.S.L.B., A.T.K.T. and A.J.M. were supported by the US NSF via RAISE-TAQS CCF 1839204. M.J.O’R. was supported by an NSF graduate fellowship via grant No. DEG-1745301; the tensor network algorithms were developed with the support of the US DOD via MURI FA9550-18-1-0095. E.Y. was supported by a Google fellowship. C.S. was supported by the US DOE via DE-SC0019374. G.K.-L.C. is a Simons Investigator in Physics and a member of the Simons Collaboration on the Many-Electron Problem. The Rigetti computations were made possible by a generous grant through Rigetti Quantum Cloud Services supported by the CQIA–Rigetti Partnership Program. We thank G. H. Low, J. R. McClean and R. Babbush for discussions, and the Rigetti team for help with the QVM and QPU simulations.
Author information
Authors and Affiliations
Contributions
M.M., C.S. and G.K.-L.C. designed the algorithms. F.G.S.L.B. established the mathematical proofs and error estimates. E.Y. and M.J.O’R. performed classical tensor network simulations. M.M., C.S. and A.T.K.T. carried out classical exact emulations. A.T.K.T. and A.J.M. designed and carried out the Rigetti QVM and QPU experiments. All authors contributed to the discussion of results and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Information.
Rights and permissions
About this article
Cite this article
Motta, M., Sun, C., Tan, A.T.K. et al. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nat. Phys. 16, 205–210 (2020). https://doi.org/10.1038/s41567-019-0704-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0704-4
This article is cited by
-
Quantum many-body simulations on digital quantum computers: State-of-the-art and future challenges
Nature Communications (2024)
-
Convergence of the quantum dynamics framework for optimization algorithm
Quantum Information Processing (2024)
-
Determination of molecular energies via variational-based quantum imaginary time evolution in a superconducting qubit system
Science China Physics, Mechanics & Astronomy (2024)
-
Error statistics and scalability of quantum error mitigation formulas
npj Quantum Information (2023)
-
Exploring finite temperature properties of materials with quantum computers
Scientific Reports (2023)