Abstract
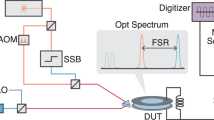
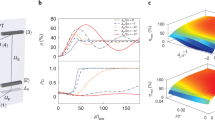
Conversion between signals in the microwave and optical domains is of great interest both for classical telecommunication and for connecting future superconducting quantum computers into a global quantum network. For quantum applications, the conversion has to be efficient, as well as operate in a regime of minimal added classical noise. While efficient conversion has been demonstrated using mechanical transducers, they have so far all operated with a substantial thermal noise background. Here, we overcome this limitation and demonstrate coherent conversion between gigahertz microwave signals and the optical telecom band with a thermal background of less than one phonon. We use an integrated, on-chip electro-optomechanical device that couples surface acoustic waves driven by a resonant microwave signal to an optomechanical crystal featuring a 2.7 GHz mechanical mode. We initialize the mechanical mode in its quantum ground state, which allows us to perform the transduction process with minimal added thermal noise, while maintaining an optomechanical cooperativity >1, so that microwave photons mapped into the mechanical resonator are effectively upconverted to the optical domain. We further verify the preservation of the coherence of the microwave signal throughout the transduction process.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data represented in the figures are available as Supplementary information files. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009).
Kurpiers, P. et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 558, 264–267 (2018).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Witmer, J. D., Hill, J. T. & Safavi-Naeini, A. H. Design of nanobeam photonic crystal resonators for a silicon-on-lithium-niobate platform. Opt. Express 24, 5876–5885 (2016).
Fan, L. et al. Superconducting cavity electro-optics: a platform for coherent photon conversion between superconducting and photonic circuits. Sci. Adv. 4, eaar4994 (2018).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 526, 101–104 (2018).
Rueda, A. et al. Efficient microwave to optical photon conversion: an electro-optical realization. Optica 3, 597–604 (2016).
O’Brien, C., Lauk, N., Blum, S., Morigi, G. & Fleischhauer, M. Interfacing superconducting qubits and telecom photons via a rare-earth-doped crystal. Phys. Rev. Lett. 113, 063603 (2014).
Hisatomi, R. et al. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016).
Stannigel, K., Rabl, P., Sørensen, A. S., Zoller, P. & Lukin, M. D. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 105, 220501 (2010).
Bochmann, J., Vainsencher, A., Awschalom, D. D. & Cleland, A. N. Nanomechanical coupling between microwave and optical photons. Nat. Phys. 9, 712–716 (2013).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014).
Bagci, T. et al. Optical detection of radio waves through a nanomechanical transducer. Nature 507, 81–85 (2014).
Van Laer, R., Patel, R. N., McKenna, T. P., Witmer, J. D. & Safavi-Naeini, A. H. Electrical driving of x-band mechanical waves in a silicon photonic circuit. APL Photon. 3, 086102 (2018).
Moaddel Haghighi, I., Malossi, N., Natali, R., Di Giuseppe, G. & Vitali, D. Sensitivity-bandwidth limit in a multimode optoelectromechanical transducer. Phys. Rev. Appl. 9, 034031 (2018).
Suchoi, O., Ella, L., Shtempluk, O. & Buks, E. Intermittency in an optomechanical cavity near a subcritical Hopf bifurcation. Phys. Rev. A 90, 033818 (2014).
Vainsencher, A., Satzinger, K. J., Peairs, G. A. & Cleland, A. N. Bi-directional conversion between microwave and optical frequencies in a piezoelectric optomechanical device. Appl. Phys. Lett. 109, 033107 (2016).
Balram, K. C., Davanço, M. I., Song, J. D. & Srinivasan, K. Coherent coupling between radiofrequency, optical and acoustic waves in piezo-optomechanical circuits. Nat. Photon. 10, 346–352 (2016).
Higginbotham, A. P. et al. Electro-optic correlations improve an efficient mechanical converter. Nat. Phys. 14, 1038–1042 (2018).
Zeuthen, E., Schliesser, A., Sørensen, A. S. & Taylor, J. M. Figures of merit for quantum transducers. Preprint at https://arxiv.org/abs/1610.01099 (2016).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Teufel, J. D. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Meenehan, S. M. et al. Pulsed excitation dynamics of an optomechanical crystal resonator near its quantum ground state of motion. Phys. Rev. X 5, 041002 (2015).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Hong, S. et al. Hanbury Brown and Twiss interferometry of single phonons from an optomechanical resonator. Science 358, 203–206 (2017).
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Riedinger, R. et al. Remote quantum entanglement between two micromechanical oscillators. Nature 556, 473–477 (2018).
Ockeloen-Korppi, C. F. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018).
Meenehan, S. M. et al. Silicon optomechanical crystal resonator at millikelvin temperatures. Phys. Rev. A 90, 011803 (2014).
Moores, B. A., Sletten, L. R., Viennot, J. J. & Lehnert, K. W. Cavity quantum acoustic device in the multimode strong coupling regime. Phys. Rev. Lett. 120, 227701 (2018).
Chan, J., Safavi-Naeini, A. H., Hill, J. T., Meenehan, S. & Painter, O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 101, 081115 (2012).
Skauli, T. et al. Improved dispersion relations for GaAs and applications to nonlinear optics. J. Appl. Phys. 94, 6447–6455 (2003).
Guha, B. et al. Surface-enhanced gallium arsenide photonic resonator with quality factor of 6 × 106. Optica 4, 218–221 (2017).
Safavi-Naeini, A. H. et al. Observation of quantum motion of a nanomechanical resonator. Phys. Rev. Lett. 108, 033602 (2012).
Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 3, 1196 (2012).
Galland, C., Sangouard, N., Piro, N., Gisin, N. & Kippenberg, T. J. Heralded single-phonon preparation, storage, and readout in cavity optomechanics. Phys. Rev. Lett. 112, 143602 (2014).
Riedinger, R. et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 530, 313–316 (2016).
Wu, M., Zeuthen, E., Balram, K. C. & Srinivasan, K. Microwave-to-optical transduction using coupled piezoelectric and optomechanical resonators. Preprint at https://arxiv.org/abs/1907.04830 (2019).
Marinković, I. et al. Optomechanical Bell test. Phys. Rev. Lett. 121, 220404 (2018).
Gustafsson, M. V. et al. Propagating phonons coupled to an artificial atom. Science 346, 207–211 (2014).
Ramp, H. et al. Elimination of thermomechanical noise in piezoelectric optomechanical crystals. Phys. Rev. Lett. 123, 093603 (2019).
Acknowledgements
We thank V. Anant, J. Davis, M. Jenkins and C. Schäfermeier for valuable discussions and support. We also acknowledge assistance from the Kavli Nanolab Delft, in particular from M. Zuiddam and C. de Boer. The sample growth was realized in the NanoLab@TU/e cleanroom facility. This project was supported by Foundation for Fundamental Research on Matter (FOM) Projectruimte grants (15PR3210, 16PR1054), the European Research Council (ERC StG Strong-Q, 676842) and by the Netherlands Organisation for Scientific Research (NWO/OCW), as part of the Frontiers of Nanoscience programme, as well as through a Vidi grant (680-47-541/994), the Gravitation programme Research Center for Integrated Nanophotonics and the ARO/LPS CQTS programme.
Author information
Authors and Affiliations
Contributions
M.F., R.S., K.S. and S.G. planned the experiment and performed the device design. M.F., R.S., C.G. and R.A.N. fabricated the sample and F.v.O. and A.F. supplied the material. M.F., R.S., A.W. and I.M. performed the measurements, while M.F., R.S., K.S. and S.G. analysed the data and wrote the manuscript with input from all authors. S.G. supervised the project.
Corresponding author
Ethics declarations
Competing interests
M.F., R.S. and S.G. declare that there is a pending patent application related to this research.
Additional information
Peer review information Nature Physics thanks David Vitali and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Forsch, M., Stockill, R., Wallucks, A. et al. Microwave-to-optics conversion using a mechanical oscillator in its quantum ground state. Nat. Phys. 16, 69–74 (2020). https://doi.org/10.1038/s41567-019-0673-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0673-7
This article is cited by
-
Continuous wideband microwave-to-optical converter based on room-temperature Rydberg atoms
Nature Photonics (2024)
-
Sub-terahertz electromechanics
Nature Electronics (2023)
-
Microwave-to-optical transduction with erbium ions coupled to planar photonic and superconducting resonators
Nature Communications (2023)
-
Quantum-enabled millimetre wave to optical transduction using neutral atoms
Nature (2023)
-
Dissipative optomechanics in high-frequency nanomechanical resonators
Nature Communications (2023)