Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Electronic correlations in twisted bilayer graphene near the magic angle

Nature Physics volume 15, pages 1174–1180 (2019)Cite this article

Subjects

An Author Correction to this article was published on 25 October 2019

This article has been updated

Abstract

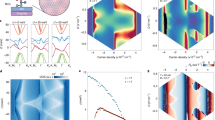
Twisted bilayer graphene with a twist angle of around 1.1° features a pair of isolated flat electronic bands and forms a platform for investigating strongly correlated electrons. Here, we use scanning tunnelling microscopy to probe the local properties of highly tunable twisted bilayer graphene devices and show that the flat bands deform when aligned with the Fermi level. When the bands are half-filled, we observe the development of gaps originating from correlated insulating states. Near charge neutrality, we find a previously unidentified correlated regime featuring an enhanced splitting of the flat bands. We describe this within a microscopic model that predicts a strong tendency towards nematic ordering. Our results provide insights into symmetry-breaking correlation effects and highlight the importance of electronic interactions for all filling fractions in twisted bilayer graphene.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Twisted bilayer graphene.
Fig. 2: Evolution of the TBG point spectrum with back-gate voltage.
Fig. 3: Model calculations and breaking of C3 symmetry.
Fig. 4: Spectroscopy at half-filling of the flat bands.

Similar content being viewed by others

Data availability

The experimental data and analyses that support the plots within this paper and the findings of this study are available from the corresponding author upon reasonable request.

Code availability

The computer codes that support the plots within this paper and the findings of this study are available from the corresponding author upon reasonable request

Change history

  • 25 October 2019

    An amendment to this paper has been published and can be accessed via a link at the top of the paper.

References

  1. Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).

    Article  ADS  Google Scholar 

  2. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    Article  ADS  Google Scholar 

  3. Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).

    ADS  Google Scholar 

  4. Trambly de Laissardière, G., Mayou, D. & Magaud, L. Localization of Dirac electrons in rotated graphene bilayers. Nano Lett. 10, 804–808 (2010).

    ADS  Google Scholar 

  5. Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).

    ADS  Google Scholar 

  6. Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Continuum model of the twisted graphene bilayer. Phys. Rev. B 86, 155449 (2012).

    ADS  Google Scholar 

  7. Fang, S. & Kaxiras, E. Electronic structure theory of weakly interacting bilayers. Phys. Rev. B 93, 235153 (2016).

    ADS  Google Scholar 

  8. Neto, A. C., Guinea, F., Peres, N. M., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).

    ADS  Google Scholar 

  9. Luican, A. et al. Single-layer behavior and its breakdown in twisted graphene layers. Phys. Rev. Lett. 106, 126802 (2011).

    ADS  Google Scholar 

  10. Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).

    Google Scholar 

  11. Brihuega, I. et al. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 109, 196802 (2012).

    ADS  Google Scholar 

  12. Ohta, T. et al. Evidence for interlayer coupling and moiré periodic potentials in twisted bilayer graphene. Phys. Rev. Lett. 109, 186807 (2012).

    ADS  Google Scholar 

  13. Havener, R. W., Liang, Y., Brown, L., Yang, L. & Park, J. Van Hove singularities and excitonic effects in the optical conductivity of twisted bilayer graphene. Nano Lett. 14, 3353–3357 (2014).

    ADS  Google Scholar 

  14. Wong, D. et al. Local spectroscopy of moiré-induced electronic structure in gate-tunable twisted bilayer graphene. Phys. Rev. B 92, 155409 (2015).

    ADS  Google Scholar 

  15. Kim, K. et al. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl Acad. Sci. USA 114, 3364–3369 (2017).

    ADS  Google Scholar 

  16. Huang, S. et al. Topologically protected helical states in minimally twisted bilayer graphene. Phys. Rev. Lett. 121, 037702 (2018).

    ADS  Google Scholar 

  17. Cao, Y. et al. Superlattice-induced insulating states and valley-protected orbits in twisted bilayer graphene. Phys. Rev. Lett. 117, 116804 (2016).

    ADS  Google Scholar 

  18. Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).

    ADS  Google Scholar 

  19. Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407 (2010).

    ADS  Google Scholar 

  20. Trambly de Laissardière, G., Mayou, D. & Magaud, L. Numerical studies of confined states in rotated bilayers of graphene. Phys. Rev. B 86, 125413 (2012).

    ADS  Google Scholar 

  21. Yan, W. et al. Angle-dependent van Hove singularities in a slightly twisted graphene bilayer. Phys. Rev. Lett. 109, 126801 (2012).

    ADS  Google Scholar 

  22. Yin, L.-J., Qiao, J.-B., Zuo, W.-J., Li, W.-T. & He, L. Experimental evidence for non-Abelian gauge potentials in twisted graphene bilayers. Phys. Rev. B 92, 081406 (2015).

    ADS  Google Scholar 

  23. Zibrov, A. A. et al. Robust fractional quantum Hall states and continuous quantum phase transitions in a half-filled bilayer graphene Landau level. Nature 549, 360–364 (2017).

    ADS  Google Scholar 

  24. Yoo, H. et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019).

    ADS  Google Scholar 

  25. Zou, L., Po, H. C., Vishwanath, A. & Senthil, T. Band structure of twisted bilayer graphene: emergent symmetries, commensurate approximants, and Wannier obstructions. Phys. Rev. B 98, 085435 (2018).

    ADS  Google Scholar 

  26. Po, H. C., Zou, L., Senthil, T. & Vishwanath, A. Faithful tight-binding models and fragile topology of magic-angle bilayer graphene. Phys. Rev. B 99, 195455 (2019).

    ADS  Google Scholar 

  27. Kang, J. & Vafek, O. Symmetry, maximally localized Wannier states, and a low-energy model for twisted bilayer graphene narrow bands. Phys. Rev. X 8, 031088 (2018).

    Google Scholar 

  28. Nam, N. N. T. & Koshino, M. Lattice relaxation and energy band modulation in twisted bilayer graphene. Phys. Rev. B 96, 075311 (2017).

    ADS  Google Scholar 

  29. Xie, M. & MacDonald, A. H. On the nature of the correlated insulator states in twisted bilayer graphene. Preprint at https://arxiv.org/abs/1812.04213 (2018).

  30. Song, Y. J. et al. High-resolution tunnelling spectroscopy of a graphene quartet. Nature 467, 185–189 (2010).

    ADS  Google Scholar 

  31. Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).

    Google Scholar 

  32. Kang, J. & Vafek, O. Strong coupling phases of partially filled twisted bilayer graphene narrow bands. Phys. Rev. Lett. 122, 246401 (2019).

    ADS  Google Scholar 

  33. Koshino, M. et al. Maximally localized Wannier orbitals and the extended Hubbard model for twisted bilayer graphene. Phys. Rev. X 8, 031087 (2018).

    Google Scholar 

  34. Guinea, F. & Walet, N. R. Electrostatic effects, band distortions, and superconductivity in twisted graphene bilayers. Proc. Natl Acad. Sci. USA 115, 13174–13179 (2018).

    ADS  Google Scholar 

  35. Hejazi, K., Liu, C., Shapourian, H., Chen, X. & Balents, L. Multiple topological transitions in twisted bilayer graphene near the first magic angle. Phys. Rev. B 99, 035111 (2019).

    ADS  Google Scholar 

  36. Lilly, M. P., Cooper, K. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Anisotropic states of two-dimensional electron systems in high Landau levels: effect of an in-plane magnetic field. Phys. Rev. Lett. 83, 824–827 (1999).

    ADS  Google Scholar 

  37. Feldman, B. E. et al. Observation of a nematic quantum Hall liquid on the surface of bismuth. Science 354, 316–321 (2016).

    ADS  Google Scholar 

  38. Huder, L. et al. Electronic spectrum of twisted graphene layers under heterostrain. Phys. Rev. Lett. 120, 156405 (2018).

    ADS  Google Scholar 

  39. Artaud, A. et al. Universal classification of twisted, strained and sheared graphene moiré superlattices. Sci. Rep. 6, 25670 (2016).

    ADS  Google Scholar 

  40. Efros, A. L. Coulomb gap in disordered systems. J. Phys. C 9, 2021–2030 (1976).

    ADS  Google Scholar 

  41. Ashoori, R. C., Lebens, J. A., Bigelow, N. P. & Silsbee, R. H. Equilibrium tunneling from the two-dimensional electron gas in GaAs: evidence for a magnetic-field-induced energy gap. Phys. Rev. Lett. 64, 681–684 (1990).

    ADS  Google Scholar 

  42. Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Coulomb barrier to tunneling between parallel two-dimensional electron systems. Phys. Rev. Lett. 69, 3804–3807 (1992).

    ADS  Google Scholar 

  43. Dial, O. E., Ashoori, R. C., Pfeiffer, L. N. & West, K. W. High-resolution spectroscopy of two-dimensional electron systems. Nature 448, 176–179 (2007).

    ADS  Google Scholar 

  44. Song, Y.-H. et al. Observation of Coulomb gap in the quantum spin Hall candidate single-layer 1T’-WTe2. Nat. Commun. 9, 4071 (2018).

    ADS  Google Scholar 

  45. Moon, B. H. et al. Soft Coulomb gap and asymmetric scaling towards metal–insulator quantum criticality in multilayer MoS2. Nat. Commun. 9, 2052 (2018).

    ADS  Google Scholar 

  46. Jung, S. et al. Evolution of microscopic localization in graphene in a magnetic field from scattering resonances to quantum dots. Nat. Phys. 7, 245–251 (2011).

    Google Scholar 

  47. Thomson, A., Chatterjee, S., Sachdev, S. & Scheurer, M. S. Triangular antiferromagnetism on the honeycomb lattice of twisted bilayer graphene. Phys. Rev. B 98, 075109 (2018).

    ADS  Google Scholar 

  48. Kerelsky, A. et al. Magic angle spectroscopy. Preprint at https://arxiv.org/abs/1812.08776 (2018).

  49. Kim, K. et al. Van der Waals heterostructures with high accuracy rotational alignment. Nano Lett. 16, 1989–1995 (2016).

    ADS  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge discussions with R. C. Ashoori, P. Jarillo-Herrero, A. Vishwanath, J. Eisenstein, A. Young and H. Beidenkopf. The STM work is in part supported by NSF DMR-1744011. Sample fabrication efforts are supported by the NSF through program NSF CAREER DMR-1753306. S.N.-P. acknowledges support from a KNI-Weathley fellowship. J.A., G.R., F.v.O., S.N.-P. and H.R. acknowledge the support of IQIM (NSF funded physics frontiers center). J.K. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG 406557161), Y.C. a Kwanjeong fellowship, F.v.O. DFG support through CRC 183, and J.A. support from the Army Research Office under grant award W911NF-17-1-0323 and the NSF through grant DMR-1723367. Y.P., A.T. and J.A. are grateful for support from the Walter Burke Institute for Theoretical Physics at Caltech.

Author information

Authors and Affiliations

  1. T. J. Watson Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA, USA

    Youngjoon Choi, Jeannette Kemmer, Harpreet Arora, Robert Polski, Yiran Zhang, Hechen Ren & Stevan Nadj-Perge

  2. Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA

    Youngjoon Choi, Jeannette Kemmer, Yang Peng, Alex Thomson, Harpreet Arora, Robert Polski, Yiran Zhang, Hechen Ren, Jason Alicea, Gil Refael, Felix von Oppen & Stevan Nadj-Perge

  3. Department of Physics, California Institute of Technology, Pasadena, CA, USA

    Youngjoon Choi, Yang Peng, Alex Thomson, Yiran Zhang, Jason Alicea & Gil Refael

  4. Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, CA, USA

    Yang Peng, Alex Thomson, Jason Alicea & Gil Refael

  5. Dahlem Center for Complex Quantum Systems and Fachbereich Physik, Freie Universität Berlin, Berlin, Germany

    Felix von Oppen

  6. National Institute for Materials Science, Tsukuba, Ibaraki, Japan

    Kenji Watanabe & Takashi Taniguchi

Authors
  1. Youngjoon Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jeannette Kemmer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yang Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Alex Thomson
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Harpreet Arora
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Robert Polski
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Yiran Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Hechen Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Jason Alicea
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Gil Refael
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Felix von Oppen
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Kenji Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Takashi Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Stevan Nadj-Perge
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Y.C., J.K. and S.N.-P. conceived the experiment. Y.C. and J.K. performed the measurements. Y.C. made the samples with the help of H.A., R.P. and Y.Z. Y.C., J.K., H.R. and S.N.-P. performed data analysis. Y.P. and A.T. developed the theory guided by F.v.O., J.A. and G.R. Y.C., J.K. and S.N.-P. wrote the manuscript with input from all authors.

Corresponding author

Correspondence to Stevan Nadj-Perge.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Additional technical and theoretical details, Supplementary Figs. 1–14, Table 1 and refs. 1–16.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Choi, Y., Kemmer, J., Peng, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019). https://doi.org/10.1038/s41567-019-0606-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0606-5

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing