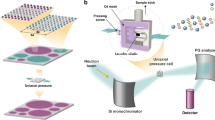
Abstract
Dissipationless charge transport is one of the defining properties of superconductors, but the interplay between dimensionality and disorder in determining the onset of dissipation remains an open theoretical and experimental problem. Here, we present measurements of the dissipation phase diagrams of superconductors in the two-dimensional limit, layer by layer, down to a monolayer in the presence of temperature (T), magnetic field (B) and current (I) in 2H-NbSe2. Our results show that the phase diagram strongly depends on the thickness even in the two-dimensional limit. At four layers we can define a finite region in the I–B phase diagram where dissipationless transport exists at T = 0. At even smaller thicknesses, this region shrinks in area until in a monolayer it approaches a single point defined by T = B = I = 0. In applied field, we show that time-dependent Ginzburg–Landau simulations that describe dissipation by vortex motion qualitatively reproduce our experimental I–B phase diagram. Last, we show that by using non-local transport and time-dependent Ginzburg–Landau calculations that we can engineer charge flow and create phase boundaries between dissipative and dissipationless transport regions in a single sample, demonstrating control over non-equilibrium states of matter.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Microscopic theory of superconductivity. Phys. Rev. 106, 162–164 (1957).
Bardeen, J. & Stephen, M. J. Theory of the motion of vortices. Phys. Rev. 140, 1197–1207 (1965).
Abrikosov, A. A. The magnetic properties of superconducting alloys. J. Phys. Chem. Solids 2, 199–208 (1957).
Tinkham, M. Introduction to Superconductivity (Dover Publication, Inc., 2004).
Fietz, W. A. & Webb, W. W. Hysteresis in superconducting alloys—temperature and field dependence of dislocation pinning in niobium alloys. Phys. Rev. 178, 657–667 (1969).
Blatter, G., Feigel’Man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
Dekker, C., Wöltgens, P. J. M., Koch, R. H., Hussey, B. W. & Gupta, A. Absence of a finite-temperature vortex-glass phase transition in two-dimensional YBa2Cu3O7–δ films. Phys. Rev. Lett. 69, 2712–2720 (1992).
Ma, M. & Lee, P. A. Localized superconductors. Phys. Rev. B 32, 5658–5667 (1985).
Anderson, P. W. Theory of dirty superconductors. J. Phys. Chem. Solids 11, 26–30 (1959).
Kapitulnik, A., Kivelson, S. A. & Spivak, B. Colloquium: anomalous metals: failed superconductors. Rev. Mod. Phys. 91, 011002 (2019).
Saito, Y., Kasahara, Y., Ye, J., Iwasa, Y. & Nojima, T. Metallic ground state in an ion-gated two-dimensional superconductor. Science 350, 409–413 (2015).
Tsen, A. W. et al. Nature of the quantum metal in a two-dimensional crystalline superconductor. Nat. Phys. 12, 208–212 (2016).
Dynes, R. C., Garno, J. P. & Rowell, J. M. Two-dimensional electrical conductivity in quench-condensed metal films. Phys. Rev. Lett. 40, 479–482 (1978).
Haviland, D. B., Liu, Y. & Goldman, A. M. Onset of superconductivity in the two-dimensional limit. Phys. Rev. Lett. 62, 2180–2183 (1989).
Gantmakher, V. F., Golubkov, M. V., Lok, J. G. S. & Geim, A. K. A. Giant negative magnetoresistance of semi-insulating amorphous indium oxide films in strong magnetic fields. J. Exp. Theor. Phys. 82, 951–958 (1996).
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2, 16094 (2016).
Tamir, I. et al. Sensitivity of the superconducting state in thin films. Sci. Adv. 5, eaau3826 (2019).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Telford, E. J. et al. Via method for lithography free contact and preservation of 2D materials. Nano Lett. 18, 1416–1420 (2018).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, H c2. III. Electron spin and spin-orbit effects. Phys. Rev. 147, 295–302 (1966).
Foner, S. & McNiff, E. J. Upper critical fields of layered superconducting NbSe2 at low temperature. Phys. Lett. A 45, 429–430 (1973).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181–1203 (1973).
Nader, A. & Monceau, P. Critical field of 2H-NbSe2 down to 50mK. Springerplus 3, 16 (2014).
Ambegaokar, V., Halperin, B. I., Nelson, D. R. & Siggia, E. D. Dynamics of superfluid films. Phys. Rev. B 21, 1806–1826 (1980).
Griessen, R., Hoekstra, A. F. T., Wen, H. H., Doornbos, G. & Schnack, H. G. Negative-μ vortex dynamics in high-Tc superconducting films. Physica C 282–287, 347–350 (1997).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 13, 1056–1068 (2017).
Ugeda, M. M. et al. Characterization of collective ground states in single-layer NbSe2. Nat. Phys. 12, 92–97 (2015).
Schneider, T. & Weyeneth, S. Suppression of the Berezinskii-Kosterlitz-Thouless and quantum phase transitions in two-dimensional superconductors by finite-size effects. Phys. Rev. B 90, 064501 (2014).
Lin, Y.-H., Nelson, J. & Goldman, A. M. Suppression of the Berezinskii-Kosterlitz-Thouless transition in 2D superconductors by macroscopic quantum tunneling. Phys. Rev. Lett. 109, 017002 (2012).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Rozhkov, A. & Stroud, D. Quantum melting of a two-dimensional vortex lattice at zero temperature. Phys. Rev. B 54, 12697–12700 (1996).
Choi, M. Y. Quantum Hall effect in ideal superconducting arrays at zero temperature. Phys. Rev. B 50, 10088–10091 (1994).
Stern, A. Quantum Hall fluid of vortices in a two-dimensional array of Josephson junctions. Phys. Rev. B 50, 10092–10106 (1994).
Onogi, T. & Doniach, S. Simulation of quantum melting of the vortex lattice and of fractional quantum Hall-like states of the quantum vortex liquid in 2D superconductors. Solid State Commun. 98, 1–5 (1996).
Feigel’man, M. V., Geshkenbein, V. B. & Larkin, A. I. Pinning and creep in layered superconductors. Physica C 167, 177–187 (1990).
Le, L. P. et al. Magnetic penetration depth in layered compound NbSe2 measured by muon spin relaxation. Physica C 185–189, 2715–2716 (1991).
Mattheiss, L. F. Band structures of transition-metal-dichalcogenide layer compounds. Phys. Rev. B 8, 3719–3740 (1973).
Acknowledgements
We thank D. Rhodes and V. Vinokour for fruitful discussions and input. This research was primarily supported by the NSF MRSEC program through Columbia in the Center for Precision Assembly of Superstratic and Superatomic Solids (DMR-1420634), the Global Research Laboratory (GRL) Program (2016K1A1A2912707) funded by the Ministry of Science, ICT and Future Planning via the National Research Foundation of Korea (NRF), and Honda Research Institute USA Inc. We acknowledge computing resources from Columbia University’s Shared Research Computing Facility project, which is supported by NIH Research Facility Improvement Grant 1G20RR030893-01, and associated funds from the New York State Empire State Development, Division of Science Technology and Innovation (NYSTAR) Contract C090171, both awarded 15 April 2010. A.J.M. and D.M.K. were supported by the Basic Energy Sciences Division of the US Department of Energy under grant DE-SC0018218. D.M.K. additionally acknowledges support by the Deutsche Forschungsgemeinschaft through the Emmy Noether program (KA 3360/2-1). This research was also supported by The Israel Science Foundation (ISF grant no. 556/17), the Minerva Foundation, Federal German Ministry for Education and Research, grant no. 71294.
Author information
Authors and Affiliations
Contributions
The experiment was designed by A.B. and E.J.T., devices fabricated by A.B., E.J.T. and A.W., data taken by A.B., E.J.T. and D.W., analysis by A.B. and E.J.T., theory and simulation by D.M.K. and A.J.M., and hBN crystals grown by K.W. and T.T. All authors contributed equally to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Physics thanks Hadar Steinberg and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–11 and Supplementary references 1–8.
Supplementary Video 1
Uniform flow, J / Jc = 0.22, B / Hc2 = 0.16.
Supplementary Video 2
Uniform flow, J / Jc = 0.43, B / Hc2 = 0.16.
Supplementary Video 3
Uniform flow, J / Jc = 0.65, B / Hc2 = 0.16.
Supplementary Video 4
Pinning, J / Jc = 0.022, B / Hc2 = 0.04.
Supplementary Video 5
Pinning, J / Jc = 0.09, B / Hc2 = 0.04.
Supplementary Video 6
Pinning, J / Jc = 0.17, B / Hc2 = 0.04.
Supplementary Video 7
Pinning, J / Jc = 0.43, B / Hc2 = 0.04.
Supplementary Video 8
Pinning, J / Jc = 0.02, B / Hc2 = 0.08.
Supplementary Video 9
Pinning, J / Jc = 0.09, B /Hc2 = 0.08.
Supplementary Video 10
Pinning, J / Jc = 0.17, B / Hc2 = 0.08.
Supplementary Video 11
Pinning, J / Jc = 0.43, B / Hc2 = 0.08.
Supplementary Video 12
Non-uniform flow, J / Jc = 0.43, B / Hc2 = 0.08.
Supplementary Video 13
Non-uniform flow, J / Jc = 0.87, B / Hc2 = 0.08.
Supplementary Video 14
Non-uniform flow, J / Jc = 1.7, B / Hc2 = 0.08.
Supplementary Video 15
Non-uniform flow, J / Jc = 2.6, B / Hc2 = 0.08.
Rights and permissions
About this article
Cite this article
Benyamini, A., Telford, E.J., Kennes, D.M. et al. Fragility of the dissipationless state in clean two-dimensional superconductors. Nat. Phys. 15, 947–953 (2019). https://doi.org/10.1038/s41567-019-0571-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0571-z
This article is cited by
-
Angle-resolved transport non-reciprocity and spontaneous symmetry breaking in twisted trilayer graphene
Nature Materials (2024)
-
Superfluid response of an atomically thin gate-tuned van der Waals superconductor
Nature Communications (2023)
-
Single-crystalline van der Waals layered dielectric with high dielectric constant
Nature Materials (2023)
-
Flux-flow instability across Berezinskii Kosterlitz Thouless phase transition in KTaO3 (111) based superconductor
Communications Physics (2023)
-
Nonreciprocal superconducting NbSe2 antenna
Nature Communications (2020)