Abstract
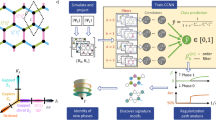
Quantum gas microscopes for ultracold atoms can provide high-resolution real-space snapshots of complex many-body systems. We implement machine learning to analyse and classify such snapshots of ultracold atoms. Specifically, we compare the data from an experimental realization of the two-dimensional Fermi–Hubbard model to two theoretical approaches: a doped quantum spin liquid state of resonating valence bond type1,2, and the geometric string theory3,4, describing a state with hidden spin order. This technique considers all available information without a potential bias towards one particular theory by the choice of an observable and can therefore select the theory that is more predictive in general. Up to intermediate doping values, our algorithm tends to classify experimental snapshots as geometric-string-like, as compared to the doped spin liquid. Our results demonstrate the potential for machine learning in processing the wealth of data obtained through quantum gas microscopy for new physical insights.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. The raw data are available in ref. 32.
Code availability
The computer codes used to generate the results of this paper are available from the corresponding author upon reasonable request.
References
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Baskaran, G., Zou, Z. & Anderson, P. The resonating valence bond state and high-T c superconductivity—a mean field theory. Solid State Commun. 63, 973–976 (1987).
Grusdt, F. et al. Parton theory of magnetic polarons: mesonic resonances and signatures in dynamics. Phys. Rev. X 8, 011046 (2018).
Grusdt, F., Bohrdt, A. & Demler, E. Microscopic spinon-chargon theory of magnetic polarons in the t-J model. Preprint at https://arxiv.org/abs/1901.01113 (2019).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Greif, D., Uehlinger, T., Jotzu, G., Tarruell, L. & Esslinger, T. Short-range quantum magnetism of ultracold fermions in an optical lattice. Science 340, 1307–1310 (2013).
Hart, R. A. et al. Observation of antiferromagnetic correlations in the Hubbard model with ultracold atoms. Nature 519, 211–214 (2015).
Cheuk, L. W. et al. Observation of spatial charge and spin correlations in the 2D Fermi–Hubbard model. Science 353, 1260–1264 (2016).
Hilker, T. A. et al. Revealing hidden antiferromagnetic correlations in doped Hubbard chains via string correlators. Science 357, 484–487 (2017).
Mazurenko, A. et al. A cold-atom Fermi–Hubbard antiferromagnet. Nature 545, 462–466 (2017).
Brown, P. T. et al. Bad metallic transport in a cold atom Fermi–Hubbard system. Science 363, 379–382 (2019).
Nichols, M. A. et al. Spin transport in a Mott insulator of ultracold fermions. Science 363, 383–387 (2019).
Salomon, G. et al. Direct observation of incommensurate magnetism in Hubbard chains. Nature 565, 56–60 (2019).
Chiu, C. S. et al. String patterns in the doped Hubbard model. Preprint at https://arxiv.org/abs/1810.03584 (2018).
Carleo, G. & Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 355, 602–606 (2017).
Glasser, I., Pancotti, N., August, M., Rodriguez, I. D. & Cirac, J. I. Neural-network quantum states, string-bond states, and chiral topological states. Phys. Rev. X 8, 011006 (2018).
Choo, K., Carleo, G., Regnault, N. & Neupert, T. Symmetries and many-body excitations with neural-network quantum states. Phys. Rev. Lett. 121, 167204 (2018).
Lu, S., Gao, X. & Duan, L.-M. Efficient representation of topologically ordered states with restricted Boltzmann machines. Phys. Rev. B 99, 155136 (2019).
Carrasquilla, J. & Melko, R. G. Machine learning phases of matter. Nat. Phys. 13, 431–434 (2017).
van Nieuwenburg, E. P. L., Liu, Y.-H. & Huber, S. D. Learning phase transitions by confusion. Nat. Phys. 13, 435–439 (2017).
Rem, B. S. et al. Identifying quantum phase transitions using artificial neural networks on experimental data. Nat. Phys. https://doi.org/10.1038/s41567-019-0554-0 (2019).
Broecker, P., Carrasquilla, J., Melko, R. G. & Trebst, S. Machine learning quantum phases of matter beyond the fermion sign problem. Sci. Rep. 7, 8823 (2017).
Ch’ng, K., Carrasquilla, J., Melko, R. G. & Khatami, E. Machine learning phases of strongly correlated fermions. Phys. Rev. X 7, 031038 (2017).
Beach, M. J. S., Golubeva, A. & Melko, R. G. Machine learning vortices at the Kosterlitz–Thouless transition. Phys. Rev. 97, 045207 (2018).
Dong, X.-Y., Pollmann, F. & Zhang, X.-F. Machine learning of quantum phase transitions. Phys. Rev. B 99, 121104 (2019).
Greitemann, J., Liu, K. & Pollet, L. Probing hidden spin order with interpretable machine learning. Phys. Rev. B 99, 060404 (2019).
Liu, K., Greitemann, J. & Pollet, L. Learning multiple order parameters with interpretable machines. Phys. Rev. B 99, 104410 (2019).
Koch-Janusz, M. & Ringel, Z. Mutual information, neural networks and the renormalization group. Nat. Phys. 14, 578–582 (2018).
Torlai, G. et al. Neural-network quantum state tomography. Nat. Phys. 14, 447–450 (2018).
Zhang, Y. et al. Machine learning in electronic-quantum-matter imaging experiments. Nature https://doi.org/10.1038/s41586-019-1319-8 (2019).
Chiu, C. S. et al. Data for ‘String patterns in the doped Hubbard model’ (Harvard Dataverse, 2019); https://doi.org/10.7910/DVN/1CSVBV
Auerbach, A. Interacting Electrons and Quantum Magnetism (Springer, 1998).
Grusdt, F., Zhu, Z., Shi, T. & Demler, E. Meson formation in mixed-dimensional t–J models. SciPost Phys. 5, 057 (2018).
Marston, J. B. & Affleck, I. Large-n limit of the Hubbard-Heisenberg model. Phys. Rev. B 39, 11538–11558 (1989).
Beran, P., Poilblanc, D. & Laughlin, R. Evidence for composite nature of quasiparticles in the 2d t-J model. Nucl. Phys. B 473, 707–720 (1996).
Baskaran, G. 3/2-Fermi liquid: the secret of high-Tc cuprates. Preprint at https://arxiv.org/abs/0709.0902 (2007).
Punk, M., Allais, A. & Sachdev, S. Quantum dimer model for the pseudogap metal. Proc. Natl Acad. Sci. USA 112, 9552–9557 (2015).
Bulaevskii, L., Nagaev, E. & Khomskii, D. A new type of auto-localized state of a conduction electron in an antiferromagnetic semiconductor. J. Exp. Theor. Phys. 27, 836 (1968).
Trugman, S. A. Interaction of holes in a Hubbard antiferromagnet and high-temperature superconductivity. Phys. Rev. B 37, 1597–1603 (1988).
Manousakis, E. String excitations of a hole in a quantum antiferromagnet and photoelectron spectroscopy. Phys. Rev. B 75, 035106 (2007).
Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016).
Acknowledgements
We thank E. Altman, I. Bloch, J. Carrasquilla, M. Kanász-Nagy, E. Khatami, F. Pollmann, A. Rosch, S. Sachdev, R. Schmidt and D. Sels for insightful discussions and M. Kanász-Nagy in addition for his Heisenberg QMC code. We acknowledge support from Harvard-MIT CUA, NSF grant no. DMR-1308435, AFOSR-MURI Quantum Phases of Matter (grant FA9550-14-1-0035), AFOSR grant no. FA9550-16-10323, DoD NDSEG, the Gordon and Betty Moore Foundation EPIQS programme and grant no. 6791, NSF GRFP and grant nos. PHY-1506203 and PHY-1734011, ONR grant no. N00014-18-1-2863, SNSF, Studienstiftung des deutschen Volkes, and the Technical University of Munich - Institute for Advanced Study, funded by the German Excellence Initiative and the European Union FP7 under grant agreement 291763, the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy–EXC-2111–390814868, the DFG grant no. KN1254/1-1, and DFG TRR80 (Project F8).
Author information
Authors and Affiliations
Contributions
A.B., F.G. and M.K. devised the method. A.B. carried out the numerical simulations and analysis. F.G. and E.D. developed the geometric string theory. C.S.C., G.J., M.X. and D.G. performed the experiments. M.G., E.D., F.G. and M.K. supervised the work. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text, Figs. 1–8 and references.
Rights and permissions
About this article
Cite this article
Bohrdt, A., Chiu, C.S., Ji, G. et al. Classifying snapshots of the doped Hubbard model with machine learning. Nat. Phys. 15, 921–924 (2019). https://doi.org/10.1038/s41567-019-0565-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0565-x
This article is cited by
-
Machine learning the microscopic form of nematic order in twisted double-bilayer graphene
Nature Communications (2023)
-
An unsupervised deep learning algorithm for single-site reconstruction in quantum gas microscopes
Communications Physics (2023)
-
U-net based vortex detection in Bose–Einstein condensates with automatic correction for manually mislabeled data
Scientific Reports (2023)
-
Quantifying hole-motion-induced frustration in doped antiferromagnets by Hamiltonian reconstruction
Communications Materials (2023)
-
Preparing quantum states by measurement-feedback control with Bayesian optimization
Frontiers of Physics (2023)