Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Avoided quasiparticle decay from strong quantum interactions

Nature Physics volume 15, pages 750–753 (2019)Cite this article

Subjects

Abstract

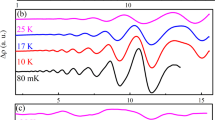
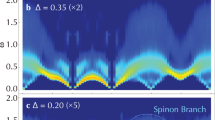
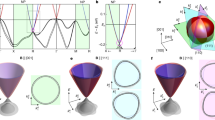
Quantum states of matter—such as solids, magnets and topological phases—typically exhibit collective excitations (for example, phonons, magnons and anyons)1. These involve the motion of many particles in the system, yet, remarkably, act like a single emergent entity—a quasiparticle. Known to be long lived at the lowest energies, quasiparticles are expected to become unstable when encountering the inevitable continuum of many-particle excited states at high energies, where decay is kinematically allowed. Although this is correct for weak interactions, we show that strong interactions generically stabilize quasiparticles by pushing them out of the continuum. This general mechanism is straightforwardly illustrated in an exactly solvable model. Using state-of-the-art numerics, we find it at work in the spin-\(1/2\) triangular-lattice Heisenberg antiferromagnet (TLHAF). This is surprising given the expectation of magnon decay in this paradigmatic frustrated magnet. Turning to existing experimental data, we identify the detailed phenomenology of avoided decay in the TLHAF material2 Ba3CoSb2O9, and even in liquid helium3,4,5,6,7,8, one of the earliest instances of quasiparticle decay9. Our work unifies various phenomena above the universal low-energy regime in a comprehensive description. This broadens our window of understanding of many-body excitations, and provides a new perspective for controlling and stabilizing quantum matter in the strongly interacting regime.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Avoided quasiparticle decay in a solvable model.
Fig. 2: Avoided decay in an Ising ladder.
Fig. 3: Avoided decay in the spin-\(\frac{{\mathbf{1}}}{{\mathbf{2}}}\) TLHAF with δ = 0.05.
Fig. 4: Avoided quasiparticle decay, genuine decay and level–continuum repulsion in experimental data for the TLHAF material Ba3CoSb2O9, piperazinium hexachlorodicuprate (PHCC) and superfluid helium.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

Code availability

Details about the DMRG code are provided in the Methods and in the Supplementary Information.

References

  1. Liesbeth, V. et al. The quasiparticle zoo. Nat. Phys. 12, 1085–1089 (2016).

    Article  Google Scholar 

  2. Ito, S. et al. Structure of the magnetic excitations in the spin-1/2 triangular-lattice Heisenberg antiferromagnet Ba3CoSb2O9. Nat. Commun. 8, 235 (2017).

    Article  ADS  Google Scholar 

  3. Woods, A. D. B. & Cowley, R. A. Structure and excitations of liquid helium. Rep. Prog. Phys. 36, 235 (1973).

    Article  Google Scholar 

  4. Donnelly, J. A. & Hills, R. N. Specific heat and dispersion curve for helium II. J. Low Temp. Phys. 44, 471–489 (1981).

    Article  ADS  Google Scholar 

  5. Glyde, H. R., Gibbs, M. R., Stirling, W. G. & Adams, M. A. Excitations in superfluid 4He beyond the roton. Europhys. Lett. 43, 422–426 (1998).

    Article  ADS  Google Scholar 

  6. Gibbs, M. R., Andersen, K. H., Stirling, W. G. & Schober, H. The collective excitations of normal and superfluid 4He: the dependence on pressure and temperature. J. Phys. Condens. Matter. 11, 603–628 (1999).

    Article  ADS  Google Scholar 

  7. Azuah, R. T., Diallo, S. O., Adams, M. A., Kirichek, O. & Glyde, H. R. Phonon–roton modes of liquid 4He beyond the roton in the porous medium MCM-41. Phys. Rev. B 88, 024510 (2013).

    Article  ADS  Google Scholar 

  8. Glyde, H. R. Excitations in the quantum liquid 4He: a review. Rep. Prog. Phys. 81, 014501 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  9. Pitaevskii, L. P. Properties of the spectrum of elementary excitations near the disintegration threshold of the excitations. J. Exp. Theor. Phys. 9, 830 (1959).

    MATH  Google Scholar 

  10. Zhitomirsky, M. E. & Chernyshev, A. L. Colloquium: spontaneous magnon decays. Rev. Mod. Phys. 85, 219–242 (2013).

    Article  ADS  Google Scholar 

  11. Stone, M. B., Zaliznyak, I. A., Hong, T., Broholm, C. L. & Reich, D. H. Quasiparticle breakdown in a quantum spin liquid. Nature 440, 187–190 (2006).

    Article  ADS  Google Scholar 

  12. Masuda, T. et al. Dynamics of composite haldane spin chains in IPA–CuCl3. Phys. Rev. Lett. 96, 047210 (2006).

    Article  ADS  Google Scholar 

  13. Oh, J. et al. Magnon breakdown in a two-dimensional triangular lattice Heisenberg antiferromagnet of multiferroic LuMnO3. Phys. Rev. Lett. 111, 257202 (2013).

    Article  ADS  Google Scholar 

  14. Robinson, N. J., Essler, F. H. L., Cabrera, I. & Coldea, R. Quasiparticle breakdown in the quasi-one-dimensional Ising ferromagnet CoNb2O6. Phys. Rev. B 90, 174406 (2014).

    Article  ADS  Google Scholar 

  15. Hong, T. et al. Field induced spontaneous quasiparticle decay and renormalization of quasiparticle dispersion in a quantum antiferromagnet. Nat. Commun. 8, 15148 (2017).

    Article  ADS  Google Scholar 

  16. Gaveau, B. & Schulman, L. S. Limited quantum decay. J. Phys. A. 28, 7359–7374 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  17. Zhitomirsky, M. E. Decay of quasiparticles in quantum spin liquids. Phys. Rev. B 73, 100404 (2006).

    Article  ADS  Google Scholar 

  18. White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).

    Article  ADS  Google Scholar 

  19. Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  20. Zaletel, M. P., Mong, R. S. K., Karrasch, C., Moore, J. E. & Pollmann, F. Time-evolving a matrix product state with long-ranged interactions. Phys. Rev. B 91, 165112 (2015).

    Article  ADS  Google Scholar 

  21. Kojima, Y. et al. Quantum magnetic properties of the spin-\({\textstyle{1 \over 2}}\) triangular-lattice antiferromagnet Ba2La2CoTe2O12. Phys. Rev. B 98, 174406 (2018).

    Article  ADS  Google Scholar 

  22. Huse, D. A. & Elser, V. Simple variational wave functions for two-dimensional Heisenberg spin-\({\textstyle{1 \over 2}}\) antiferromagnets. Phys. Rev. Lett. 60, 2531–2534 (1988).

    Article  ADS  Google Scholar 

  23. Bernu, B., Lhuillier, C. & Pierre, L. Signature of Néel order in exact spectra of quantum antiferromagnets on finite lattices. Phys. Rev. Lett. 69, 2590–2593 (1992).

    Article  ADS  Google Scholar 

  24. Chernyshev, A. L. & Zhitomirsky, M. E. Spin waves in a triangular lattice antiferromagnet: decays, spectrum renormalization and singularities. Phys. Rev. B 79, 144416 (2009).

    Article  ADS  Google Scholar 

  25. Zheng, W., Fjærestad, J. O., Singh, R. R. P., McKenzie, R. H. & Coldea, R. Excitation spectra of the spin- \({\textstyle{1 \over 2}}\) triangular-lattice Heisenberg antiferromagnet. Phys. Rev. B 74, 224420 (2006).

    Article  ADS  Google Scholar 

  26. Mourigal, M., Fuhrman, W. T., Chernyshev, A. L. & Zhitomirsky, M. E. Dynamical structure factor of the triangular-lattice antiferromagnet. Phys. Rev. B 88, 094407 (2013).

    Article  ADS  Google Scholar 

  27. Gohlke, M., Verresen, R., Moessner, R. & Pollmann, F. Dynamics of the Kitaev–Heisenberg model. Phys. Rev. Lett. 119, 157203 (2017).

    Article  ADS  Google Scholar 

  28. Verresen, R., Pollmann, F. & Moessner, R. Quantum dynamics of the square-lattice Heisenberg model. Phys. Rev. B 98, 155102 (2018).

    Article  ADS  Google Scholar 

  29. Plumb, K. W. et al. Quasiparticle-continuum level repulsion in a quantum magnet. Nat. Phys. 12, 224–229 (2016).

    Article  Google Scholar 

  30. Bhatt, R. N. & McMillan, W. L. Theory of anomalous dispersion in liquid He4. Phys. Rev. A 10, 1591–1597 (1974).

    Article  ADS  Google Scholar 

  31. Demkov, Y. N. & Osherov, V. I. Stationary and nonstationary problems in quantum mechanics that can be solved by means of contour integration. Sov. J. Exp. Theor. Phys. 26, 916 (1968).

    ADS  Google Scholar 

  32. Basko, D. M. Landau–Zener–Stueckelberg physics with a singular continuum of states. Phys. Rev. Lett. 118, 016805 (2017).

    Article  ADS  Google Scholar 

  33. Zimering, S. Some asymptotic behavior of Stieltjes transforms. J. Math. Phys. 10, 181–183 (1969).

    Article  ADS  MathSciNet  Google Scholar 

  34. White, S. R. & Affleck, I. Spectral function for the S = 1 Heisenberg antiferromagetic chain. Phys. Rev. B 77, 134437 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors thank R. Coldea, S. Parameswaran and S. Chernyshev for discussions, and the latter for detailed comments on the manuscript. The authors also thank I. Khaymovich for pointing out the inspiring refs. 31,32. R.V. was supported by the German Research Foundation (DFG) through the Collaborative Research Center SFB 1143. F.P. acknowledges support from DFG Research Unit FOR 1807 through grant no. PO 1370/2-1, TRR80, Nanosystems Initiative Munich (NIM) by the German Excellence Initiative, the DFG under Germany’s Excellence Strategy EXC-2111-390814868, and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 771537). This research was supported in part by the National Science Foundation under grant no. NSF PHY-1748958 and by the Heising–Simons Foundation.

Author information

Authors and Affiliations

  1. Max-Planck-Institute for the Physics of Complex Systems, Dresden, Germany

    Ruben Verresen & Roderich Moessner

  2. Department of Physics, Technische Universität München, Garching, Germany

    Ruben Verresen & Frank Pollmann

  3. Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA, USA

    Ruben Verresen

  4. Munich Center for Quantum Science and Technology (MCQST), Munich, Germany

    Frank Pollmann

Authors
  1. Ruben Verresen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Roderich Moessner
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Frank Pollmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally to this work.

Corresponding author

Correspondence to Ruben Verresen.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Text and Supplementary Figs. 1–7.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Verresen, R., Moessner, R. & Pollmann, F. Avoided quasiparticle decay from strong quantum interactions. Nat. Phys. 15, 750–753 (2019). https://doi.org/10.1038/s41567-019-0535-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0535-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing