Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Wound healing coordinates actin architectures to regulate mechanical work

Nature Physics volume 15, pages 696–705 (2019)Cite this article

Subjects

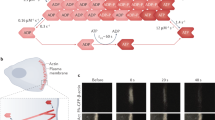
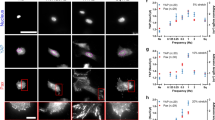
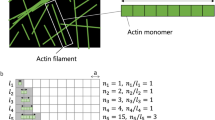
Abstract

How cells with diverse morphologies and cytoskeletal architectures modulate their mechanical behaviours to drive robust collective motion within tissues is poorly understood. During wound repair within epithelial monolayers in vitro, cells coordinate the assembly of branched and bundled actin networks to regulate the total mechanical work produced by collective cell motion. Using traction force microscopy, we show that the balance of actin network architectures optimizes the wound closure rate and the magnitude of the mechanical work. These values are constrained by the effective power exerted by the monolayer, which is conserved and independent of actin architectures. Using a cell-based physical model, we show that the rate at which mechanical work is done by the monolayer is limited by the transformation between actin network architectures and differential regulation of cell–substrate friction. These results and our proposed mechanisms provide a robust physical model for how cells collectively coordinate their non-equilibrium behaviours to dynamically regulate tissue-scale mechanical output.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Monolayer viscoelasticity depends on substrate rigidity.
Fig. 2: F-actin architecture varies with wound size and with substrate stiffness.
Fig. 3: Purse string coordinates with lamellipodia to maintain closure time.
Fig. 4: Mechanical work, but not effective power, is architecture dependent.
Fig. 5: F-actin is conserved during lamellipodial to purse string transition.
Fig. 6: Differential friction is necessary to balance effective power.

Similar content being viewed by others

Data availability

Data that support plots and other findings within this manuscript are available from the corresponding authors upon reasonable request.

Code availability

Custom codes that were used to analyse experimental data within this manuscript are available from the corresponding authors upon reasonable request.

References

  1. Haigo, S. L. & Bilder, D. Global tissue revolutions in a morphogenetic movement controlling elongation. Science 331, 1071–1074 (2011).

    Article  ADS  Google Scholar 

  2. Edwards, K. A., Demsky, M., Montague, R. A., Weymouth, N. & Kiehart, D. P. GFP-moesin illuminates actin cytoskeleton dynamics in living tissue and demonstrates cell shape changes during morphogenesis in Drosophila. Dev. Biol. 191, 103–117 (1997).

    Article  Google Scholar 

  3. Simske, J. S. & Hardin, J. Getting into shape: epidermal morphogenesis in Caenorhabditis elegans embryos. Bioessays 23, 12–23 (2001).

    Article  Google Scholar 

  4. Nabeshima, K., Inoue, T., Shimao, Y., Kataoka, H. & Koono, M. Cohort migration of carcinoma cells: differentiated colorectal carcinoma cells move as coherent cell clusters or sheets. Histol. Histopathol. 14, 1183–1197 (1999).

    Google Scholar 

  5. Friedl, P. et al. Migration of coordinated cell clusters in mesenchymal and epithelial cancer explants in vitro. Cancer Res. 55, 4557–4560 (1995).

    Google Scholar 

  6. Gaggioli, C. et al. Fibroblast-led collective invasion of carcinoma cells with differing roles for RhoGTPases in leading and following cells. Nat. Cell Biol. 9, 1392–1400 (2007).

    Article  Google Scholar 

  7. Friedl, P. & Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell. Biol. 10, 445–457 (2009).

    Article  Google Scholar 

  8. Trepat, X. et al. Physical forces during collective cell migration. Nat. Phys. 5, 426–430 (2009).

    Article  Google Scholar 

  9. Tambe, D. T. et al. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 10, 469–475 (2011).

    Article  ADS  Google Scholar 

  10. Maruthamuthu, V., Sabass, B., Schwarz, U. S. & Gardel, M. L. Cell–ECM traction force modulates endogenous tension at cell–cell contacts. Proc. Natl Acad. Sci. USA 108, 4708–4713 (2011).

    Article  ADS  Google Scholar 

  11. Schmidt, G. H., Winton, D. J. & Ponder, B. A. Development of the pattern of cell renewal in the crypt-villus unit of chimaeric mouse small intestine. Development 103, 785–790 (1988).

    Google Scholar 

  12. Brugues, A. et al. Forces driving epithelial wound healing. Nat. Phys. 10, 684–691 (2014).

    Article  Google Scholar 

  13. Zhao, M., Song, B., Pu, J., Forrester, J. V. & McCaig, C. D. Direct visualization of a stratified epithelium reveals that wounds heal by unified sliding of cell sheets. FASEB J. 17, 397–406 (2003).

    Article  Google Scholar 

  14. Bement, W. M., Mandato, C. A. & Kirsch, M. N. Wound-induced assembly and closure of an actomyosin purse string in Xenopus oocytes. Curr. Biol. 9, 579–587 (1999).

    Article  Google Scholar 

  15. Farooqui, R. & Fenteany, G. Multiple rows of cells behind an epithelial wound edge extend cryptic lamellipodia to collectively drive cell-sheet movement. J. Cell Sci. 118, 51–63 (2005).

    Article  Google Scholar 

  16. Nusrat, A., Delp, C. & Madara, J. L. Intestinal epithelial restitution - characterization of a cell-culture model and mapping of cytoskeletal elements in migrating cells. J. Clin. Investig. 89, 1501–1511 (1992).

    Article  Google Scholar 

  17. Tamada, M., Perez, T. D., Nelson, W. J. & Sheetz, M. P. Two distinct modes of myosin assembly and dynamics during epithelial wound closure. J. Cell Biol. 176, 27–33 (2007).

    Article  Google Scholar 

  18. Bement, W. M., Forscher, P. & Mooseker, M. S. A novel cytoskeletal structure involved in purse string wound closure and cell polarity maintenance. J. Cell Biol. 121, 565–578 (1993).

    Article  Google Scholar 

  19. Murrell, M., Kamm, R. & Matsudaira, P. Substrate viscosity enhances correlation in epithelial sheet movement. Biophys. J. 101, 297–306 (2011).

    Article  ADS  Google Scholar 

  20. Anon, E. et al. Cell crawling mediates collective cell migration to close undamaged epithelial gaps. Proc. Natl Acad. Sci. USA 109, 10891–10896 (2012).

    Article  ADS  Google Scholar 

  21. Ravasio, A. et al. Gap geometry dictates epithelial closure efficiency. Nat. Commun. 6, 7683 (2015).

    Article  ADS  Google Scholar 

  22. Vedula, S. R. et al. Mechanics of epithelial closure over non-adherent environments. Nat. Commun. 6, 6111 (2015).

    Article  ADS  Google Scholar 

  23. Califano, J. P. & Reinhart-King, C. A. Substrate stiffness and cell area predict cellular traction stresses in single cells and cells in contact. Cell Mol. Bioeng. 3, 68–75 (2010).

    Article  Google Scholar 

  24. Han, S. J., Bielawski, K. S., Ting, L. H., Rodriguez, M. L. & Sniadecki, N. J. Decoupling substrate stiffness, spread area, and micropost density: a close spatial relationship between traction forces and focal adhesions. Biophys. J. 103, 640–648 (2012).

    Article  ADS  Google Scholar 

  25. Harkness, T. et al. High-content imaging with micropatterned multiwell plates reveals influence of cell geometry and cytoskeleton on chromatin dynamics. Biotechnol. J. 10, 1555–1567 (2015).

    Article  Google Scholar 

  26. Limouze, J., Straight, A. F., Mitchison, T. & Sellers, J. R. Specificity of blebbistatin, an inhibitor of myosin II. J. Muscle Res. Cell Motil. 25, 337–341 (2004).

    Article  Google Scholar 

  27. Rizvi, S. A. et al. Identification and characterization of a small molecule inhibitor of formin-mediated actin assembly. Chem. Biol. 16, 1158–1168 (2009).

    Article  Google Scholar 

  28. Nolen, B. J. et al. Characterization of two classes of small molecule inhibitors of Arp2/3 complex. Nature 4640, 1031–1034 (2009).

    Article  ADS  Google Scholar 

  29. Burnette, D. T. et al. A role for actin arcs in the leading-edge advance of migrating cells. Nat. Cell Biol. 13, 371–U388 (2011).

    Article  Google Scholar 

  30. Honda, H. & Eguchi, G. How much does the cell boundary contract in a monolayered cell sheet. J. Theor. Biol. 84, 575–588 (1980).

    Article  Google Scholar 

  31. Farhadifar, R., Roper, J. C., Algouy, B., Eaton, S. & Julicher, F. The influence of cell mechanics, cell–cell interactions, and proliferation on epithelial packing. Curr. Biol. 17, 2095–2104 (2007).

    Article  Google Scholar 

  32. Fletcher, A. G., Osterfield, M., Baker, R. E. & Shvartsman, S. Y. Vertex models of epithelial morphogenesis. Biophys. J. 106, 2291–2304 (2014).

    Article  ADS  Google Scholar 

  33. Krzyszczyk, P. & Wolgemuth, C. W. Mechanosensing can result from adhesion molecule dynamics. Biophys. J. 101, L53–L55 (2011).

    Article  Google Scholar 

  34. Cochet-Escartin, O., Ranft, J., Silberzan, P. & Marcq, P. Border forces and friction control epithelial closure dynamics. Biophys. J. 106, 65–73 (2014).

    Article  ADS  Google Scholar 

  35. Brown, R. A., Prajapati, R., McGrouther, D. A., Yannas, I. V. & Eastwood, M. Tensional homeostasis in dermal fibroblasts: mechanical responses to mechanical loading in three-dimensional substrates. J. Cell. Physiol. 175, 323–332 (1998).

    Article  Google Scholar 

  36. Chien, S. Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. Am. J. Physiol. Heart Circ. Physiol. 292, H1209–H1224 (2007).

    Article  Google Scholar 

  37. du Roure, O. et al. Force mapping in epithelial cell migration. Proc. Natl Acad. Sci. USA 102, 2390–2395 (2005).

    Article  ADS  Google Scholar 

  38. Mertz, A. F. et al. Cadherin-based intercellular adhesions organize epithelial cell-matrix traction forces. Proc. Natl Acad. Sci. USA 110, 842–847 (2013).

    Article  ADS  Google Scholar 

  39. Mertz, A. F. et al. Scaling of traction forces with the size of cohesive cell colonies. Phys. Rev. Lett. 108, 198101 (2012).

    Article  ADS  Google Scholar 

  40. Bi, D., Yang, X., Marchetti, M. C. & Manning, M. L. Motility-driven glass and jamming transitions in biological tissues. Phys. Rev. X 6, 021011 (2016).

    Google Scholar 

  41. Razzell, W., Wood, W. & Martin, P. Recapitulation of morphogenetic cell shape changes enables wound re-epithelialisation. Development 141, 1814–1820 (2014).

    Article  Google Scholar 

  42. Staddon, M. F. et al. Cooperation of dual modes of cell motility promotes epithelial stress relaxation to accelerate wound healing. PLoS Comput. Biol. 14, e1006502 (2018).

    Article  Google Scholar 

  43. Mitrossilis, D. et al. Single-cell response to stiffness exhibits muscle-like behavior. Proc. Natl Acad. Sci. USA 106, 18243–18248 (2009).

    Article  ADS  Google Scholar 

  44. Yeung, T. et al. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton 60, 24–34 (2005).

    Article  Google Scholar 

  45. Sabass, B., Gardel, M. L., Waterman, C. M. & Schwarz, U. S. High resolution traction force microscopy based on experimental and computational advances. Biophys. J. 94, 207–220 (2008).

    Article  Google Scholar 

  46. Thevenaz, P., Ruttimann, U. E. & Unser, M. A pyramid approach to subpixel registration based on intensity. IEEE Trans. Image Process. 7, 27–41 (1998).

    Article  ADS  Google Scholar 

  47. Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).

    Article  Google Scholar 

  48. Brakke, K. A. The surface evolver. Exp. Math. 1, 141–165 (1992).

    Article  MathSciNet  Google Scholar 

  49. Kuipers, D. et al. Epithelial repair is a two-stage process driven first by dying cells and then by their neighbours. J. Cell Sci. 127, 1229–1241 (2014).

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge funding ARO MURI W911NF-14-1-0403 to M.P.M., D.R.K., C.S., V.A. and A.P.T. D.S.S. acknowledges support from National Science Foundation (NSF) Fellowship grant number DGE1122492. We acknowledge funding CMMI-1525316 and NIH RO1 GM126256 to M.P.M. and NIH U54 CA209992 to M.P.M. and M.S.Y. We also acknowledge fellowship support from the Yale Endowed Fund to V.A. M.F.S. is supported by a UK Engineering and Physical Sciences Research Council (EPSRC) PhD studentship at University College London (UCL). S.B. is supported by Royal Society Tata University Research Fellowship grant number URF/R1/180187, and acknowledges support from a Strategic Fellowship at UCL. S.B. and M.P.M. also acknowledge support from Human Frontiers Science Program (HFSP) grant number RGY0073/2018. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the NSF, NIH, HFSP, Royal Society, or EPSRC.

Author information

Author notes

  1. These authors contributed equally: Visar Ajeti, A. Pasha Tabatabai.

Authors and Affiliations

  1. Department of Biomedical Engineering, Yale University, New Haven, CT, USA

    Visar Ajeti, A. Pasha Tabatabai, M. Sulaiman Yousafzai & Michael P. Murrell

  2. Systems Biology Institute, Yale University, West Haven, CT, USA

    Visar Ajeti, A. Pasha Tabatabai, Daniel S. Seara, M. Sulaiman Yousafzai & Michael P. Murrell

  3. Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI, USA

    Andrew J. Fleszar

  4. Department of Physics and Astronomy, Institute for the Physics of Living Systems, University College London, London, UK

    Michael F. Staddon & Shiladitya Banerjee

  5. Department of Physics, Yale University, New Haven, CT, USA

    Daniel S. Seara & Michael P. Murrell

  6. Department of Molecular Genetics and Cell Biology, University of Chicago, Chicago, IL, USA

    Cristian Suarez & David R. Kovar

  7. Department of Physics, Northeastern University, 111 Dana Research Center, Boston, MA, USA

    Dapeng Bi

Authors
  1. Visar Ajeti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Pasha Tabatabai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Andrew J. Fleszar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Michael F. Staddon
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Daniel S. Seara
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Cristian Suarez
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. M. Sulaiman Yousafzai
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Dapeng Bi
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. David R. Kovar
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Shiladitya Banerjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Michael P. Murrell
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.P.M. designed and conceived the experimental work. S.B. designed and conceived the computational model. V.A., A.P.T., A.F. and M.S.Y. acquired experimental data. M.P.M., A.P.T., D.S.S., C.S. and V.A. analysed experimental data. M.F.S. implemented the model and performed simulations. D.B. provided computational tools and design. M.P.M. and S.B. contributed analytical tools. M.P.M., A.P.T., S.B., M.F.S. and D.K. wrote the paper. V.A. and A.P.T. are equal co-first authors, listed alphabetically, and A.J.F. and M.F.S. are equal co-second authors, listed alphabetically.

Corresponding author

Correspondence to Michael P. Murrell.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Journal peer review information: Nature Physics thanks Dimitrije Stamenovic and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Notes 1–4, Supplementary Equations, Supplementary Figures 1–10 and Supplementary References 1–10.

Reporting Summary

Supplementary Video 1

Retraction of cell monolayer after ablation. DIC images of cell monolayer during wounding. Radial velocity vectors calculated from PIV measurements of DIC show a net outward flow, caused by a retraction of the monolayer. Scale bar is 20 μm.

Supplementary Video 2

Depolymerization of F-actin during monolayer retraction. Caco2 cell transiently transfected with LifeAct-GFP. Upon ablation, the cell retracts and forms both lamellipodial and purse string F-actin architectures. Concomitantly, cytoskeletal F-actin structures depolymerize. Scale bar is 25 μm.

Supplementary Video 3

Assembly of lamellipodia and purse string—early times. Ablation of epithelial sheets of Caco2 cells singly transfected with LifeAct-GFP. At the wound boundary, a cell assembles F-actin lamellipodium (left) and purse string (right) architectures. Scale bar is 20 μm.

Supplementary Video 4

Assembly of lamellipodia and purse string—late times. Ablation of epithelial sheets of Caco2 cells singly transfected with LifeAct-GFP. At the wound boundary, a cell assembles F-actin lamellipodial (left) and purse string (right) architectures. Scale bar is 20 μm.

Supplementary Video 5

Enhanced contrast of purse string during closure. Ablation of epithelial sheets of Caco2 cells singly transfected with LifeAct-GFP. At the wound boundary, a cell assembles an F-actin purse string architecture. Actin intensity is scaled to show details of the actin purse string. Scale bar is 20 μm.

Supplementary Video 6

Pharmacological controls. Wounds induced on 12.2 kPa substrates. CK666 and SMIFH2 inhibitors (left) and calcium–magnesium switch (right). Scale bar is 20 μm.

Supplementary Video 7

Wound closure for pharmacological perturbations. Wounds induced on 24 kPa substrates for the control (left), SMIFH2 (middle) and CK666 (right). Scale bar is 20 μm.

Supplementary Video 8

Pharmacological controls. Wounds induced on 12.2 kPa substrates. Nocodazole treatment to interfere with microtubule polymerization (left) and Y-27632 to biochemically inhibit ROCK1 and ROCK2 protein kinases (right). Scale bar is 20 μm.

Supplementary Video 9

Vertex model wound closure. Simulated wounds where the cells at the leading edge switch from lamellipodial crawling to purse string with a rate kPS. kPS = 1.5 h–1 (left) leads to primarily lamellipodial closure, whereas kPS = 3.5 h–1 (right) results in a complete transition to purse-string closure.

Supplementary Video 10

Instance of lamellipodial cell overcoming the leading purse string. Actin fluorescence images and traction stress maps for the rare case of a lamellipodial protrusion of a sub-marginal cell passing the purse string. Stresses localize to actin structures at wound edge. Scale bar is 20 μm.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ajeti, V., Tabatabai, A.P., Fleszar, A.J. et al. Wound healing coordinates actin architectures to regulate mechanical work. Nat. Phys. 15, 696–705 (2019). https://doi.org/10.1038/s41567-019-0485-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0485-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing