Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

From networks to optimal higher-order models of complex systems

Nature Physics volume 15, pages 313–320 (2019)Cite this article

Subjects

Abstract

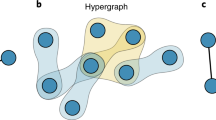
Rich data are revealing that complex dependencies between the nodes of a network may not be captured by models based on pairwise interactions. Higher-order network models go beyond these limitations, offering new perspectives for understanding complex systems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Different approaches to model an ego network with higher-order dependencies between nodes.
Fig. 2: Non-Markovian higher-order models can better capture the topology of paths in complex systems.
Fig. 3: Community detection of paths can capture overlapping communities.
Fig. 4: Non-Markovian paths change the centrality of nodes in time-stamped social network data.
Fig. 5: De Bruijn graphs with m dimensions help generalize network analytic methods to higher-order models.
Fig. 6: Non-Markovian paths in networked systems influence the evolution of diffusion processes.

Similar content being viewed by others

References

  1. Newman, M. E. The structure and function of complex networks. SIAM Rev. 45, 167–256 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  2. Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D. U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  3. Newman, M. E. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74, 036104 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  4. Estrada, E. & Higham, D. J. Network properties revealed through matrix functions. SIAM Rev. 52, 696–714 (2010).

    Article  MathSciNet  Google Scholar 

  5. Porter, M. A. & Gleeson, J. P. Dynamical Systems on Networks: A Tutorial (Springer, 2006).

  6. Even, S. Graph Algorithms (Cambridge Univ. Press, 2011).

  7. Seary, A. J. & Richards, W. D. Spectral methods for analyzing and visualizing networks: an introduction. In Dynamic Social Network Modeling and Analysis: Workshop Summary and Papers 209–228 (The National Academies Press, 2000).

  8. De Domenico, M., Granell, C., Porter, M. A. & Arenas, A. The physics of spreading processes in multilayer networks. Nat. Phys. 12, 901–906 (2016).

    Article  Google Scholar 

  9. Holme, P. & Saramäki, J. Temporal networks. Phys. Rep. 519, 97–125 (2012).

    Article  ADS  Google Scholar 

  10. Scholtes, I. et al. Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat. Commun. 5, 5024 (2014).

    Article  Google Scholar 

  11. Scholtes, I., Wider, N. & Garas, A. Higher-order aggregate networks in the analysis of temporal networks: path structures and centralities. Eur. Phys. J. B 89, 61 (2016).

    Article  ADS  Google Scholar 

  12. Rosvall, M., Esquivel, A. V., Lancichinetti, A., West, J. D. & Lambiotte, R. Memory in network flows and its effects on spreading dynamics and community detection. Nat. Commun. 5, 5630 (2014).

    Article  Google Scholar 

  13. Benson, A. R. Three hypergraph eigenvector centralities. Preprint at https://arxiv.org/abs/1807.09644 (2018).

  14. Benson, A. R., Gleich, D. F. & Leskovec, J. Higher-order organization of complex networks. Science 353, 163–166 (2016).

    Article  ADS  Google Scholar 

  15. Xu, J., Wickramarathne, T. L. & Chawla, N. V. Representing higher-order dependencies in networks. Sci. Adv. 2, e1600028 (2016).

    Article  ADS  Google Scholar 

  16. Peixoto, T. P. & Rosvall, M. Modelling sequences and temporal networks with dynamic community structures. Nat. Commun. 8, 582 (2017).

    Article  ADS  Google Scholar 

  17. Scholtes, I. When is a network a network? Multi-order graphical model selection in pathways and temporal networks. In Proc. 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ‘17 1037–1046 (ACM, 2017).

  18. Schaub, M. T., Benson, A. R., Horn, P., Lippner, G. & Jadbabaie, A. Random walks on simplicial complexes and the normalized hodge laplacian. Preprint at https://arxiv.org/abs/1807.05044 (2018).

  19. Kivelä, M. et al. Multilayer networks. J. Complex Netw. 2, 203–271 (2014).

    Article  Google Scholar 

  20. Arenas, A., Fernandez, A., Fortunato, S. & Gomez, S. Motif-based communities in complex networks. J. Phys. A 41, 224001 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  21. Jiang, X., Lim, L.-H., Yao, Y. & Ye, Y. Statistical ranking and combinatorial hodge theory. Math. Program. 127, 203–244 (2011).

    Article  MathSciNet  Google Scholar 

  22. Petri, G., Scolamiero, M., Donato, I. & Vaccarino, F. Topological strata of weighted complex networks. PLoS ONE 8, e66506 (2002).

    Article  Google Scholar 

  23. Cardillo, A. et al. Modeling the multi-layer nature of the European Air Transport Network: resilience and passengers re-scheduling under random failures. Eur. Phys. J. Spec. Top. 215, 23–33 (2013).

    Article  Google Scholar 

  24. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).

    Article  ADS  Google Scholar 

  25. Battiston, S., Caldarelli, G. & D’Errico, M. in Interconnected Networks (ed. Garas, A.) 195–229 (Springer, 2016).

  26. Moreno, J. L. Who Shall Survive? A New Approach to the Problem of Human Interrelations (Beacon House, 1934).

  27. Mucha, P. J., Richardson, T., Macon, K., Porter, M. A. & Onnela, J.-P. Community structure in time-dependent, multiscale, and multiplex networks. Science 328, 876–878 (2010).

    Article  ADS  MathSciNet  Google Scholar 

  28. Halu, A., Mondragón, R. J., Panzarasa, P. & Bianconi, G. Multiplex PageRank. PLoS ONE 8, e78293 (2013).

    Article  ADS  Google Scholar 

  29. De Domenico, M., Solé-Ribalta, A., Omodei, E., Gómez, S. & Arenas, A. Ranking in interconnected multilayer networks reveals versatile nodes. Nat. Commun. 6, 6868 (2015).

    Article  Google Scholar 

  30. Granovetter, M. S. The strength of weak ties. Am. J. Sociol. 78, 1360–1380 (1973).

    Article  Google Scholar 

  31. Patania, A., Petri, G. & Vaccarino, F. The shape of collaborations. EPJ Data Sci. 6, 18 (2017).

    Article  Google Scholar 

  32. Mangan, S. & Alon, U. Structure and function of the feed-forward loop network motif. Proc. Natl Acad. Sci. USA 100, 11980–11985 (2003).

    Article  ADS  Google Scholar 

  33. Paranjape, A., Benson, A. R. & Leskovec, J. Motifs in temporal networks. In Proc. 10th ACM International Conference on Web Search and Data Mining 601–610 (ACM, 2017).

  34. Levine, J. M., Bascompte, J., Adler, P. B. & Allesina, S. Beyond pairwise mechanisms of species coexistence in complex communities. Nature 546, 56–64 (2017).

    Article  ADS  Google Scholar 

  35. Kuzmin, E. et al. Systematic analysis of complex genetic interactions. Science 360, eaao1729 (2018).

    Article  Google Scholar 

  36. Ghoshal, G., Zlatić, V., Caldarelli, G. & Newman, M. E. Random hypergraphs and their applications. Phys. Rev. E 79, 066118 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  37. Mukherjee, S. & Steenbergen, J. Random walks on simplicial complexes and harmonics. Random Struct. Algorithms 49, 379–405 (2016).

    Article  MathSciNet  Google Scholar 

  38. Boissonnat, J.-D., Chazal, F. & Yvinec, M. Geometric and Topological Inference Vol. 57 (Cambridge Univ. Press, 2018).

  39. Liljeros, F., Giesecke, J. & Holme, P. The contact network of inpatients in a regional healthcare system. A longitudinal case study. Math. Popul. Stud. 14, 269–284 (2007).

    Article  MathSciNet  Google Scholar 

  40. Karsai, M., Kaski, K. & Kertész, J. Correlated dynamics in egocentric communication networks. PLoS ONE 7, e40612 (2012).

    Article  ADS  Google Scholar 

  41. Pfitzner, R., Scholtes, I., Garas, A., Tessone, C. J. & Schweitzer, F. Betweenness preference: quantifying correlations in the topological dynamics of temporal networks. Phys. Rev. Lett. 110, 198701 (2013).

    Article  ADS  Google Scholar 

  42. Wei, W. & Carley, K. M. Measuring temporal patterns in dynamic social networks. ACM Trans. Knowl. Discov. Data 10, 9 (2015).

    Article  Google Scholar 

  43. Lentz, H. H. K., Selhorst, T. & Sokolov, I. M. Unfolding accessibility provides a macroscopic approach to temporal networks. Phys. Rev. Lett. 110, 118701 (2013).

    Article  ADS  Google Scholar 

  44. Koher, A., Lentz, H. H. K., Hövel, P. & Sokolov, I. M. Infections on temporal networks — a matrix-based approach. PLoS ONE 11, e0151209 (2016).

    Article  Google Scholar 

  45. Matamalas, J. T., De Domenico, M. & Arenas, A. Assessing reliable human mobility patterns from higher order memory in mobile communications. J. R. Soc. Interface 13, 20160203 (2016).

    Article  Google Scholar 

  46. Asztalos, A. & Toroczkai, Z. Network discovery by generalized random walks. Europhys. Lett. 92, 50008 (2010).

    Article  ADS  Google Scholar 

  47. Palla, G. et al. Complex clinical pathways of an autoimmune disease. J. Complex Netw. 6, 206–214 (2017).

    Article  Google Scholar 

  48. Box, G. E., Jenkins, G. M. & Reinsel, G. C. Time Series Analysis: Forecasting and Control (John Wiley & Sons, 2013).

  49. Salzberg, S. L., Delcher, A. L., Kasif, S. & White, O. Microbial gene identification using interpolated Markov models. Nucleic Acids Res. 26, 544–548 (1998).

    Article  Google Scholar 

  50. Benson, A. R., Gleich, D. F. & Lim, L.-H. The spacey random walk: a stochastic process for higher-order data. SIAM Rev. 59, 321–345 (2017).

    Article  MathSciNet  Google Scholar 

  51. Lu, X., Wetter, E., Bharti, N., Tatem, A. J. & Bengtsson, L. Approaching the limit of predictability in human mobility. Sci. Rep. 3, 2923 (2013).

    Article  ADS  Google Scholar 

  52. Chierichetti, F., Kumar, R., Raghavan, P. & Sarlós, T. Are web users really Markovian? In Proc. 21st Int. Conf. on World Wide Web 609–618 (ACM, 2012).

  53. Singer, P., Helic, D., Taraghi, B. & Strohmaier, M. Detecting memory and structure in human navigation patterns using Markov chain models of varying order. PLoS ONE 9, e114952 (2014).

    Article  Google Scholar 

  54. Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948).

    Article  MathSciNet  Google Scholar 

  55. Dunning, T. Statistical Identification of Language Technical Report (Computing Research Laboratory, 1994).

  56. Edler, D. et al. Mapping higher-order network flows in memory and multilayer networks with Infomap. Algorithms 10, 112 (2017).

    Article  MathSciNet  Google Scholar 

  57. Fortunato, S. Community detection in graphs. Phys. Rep. 486, 75–174 (2010).

    Article  ADS  MathSciNet  Google Scholar 

  58. Persson, C., Bohlin, L., Edler, D. & Rosvall, M. Maps of sparse Markov chains efficiently reveal community structure in network flows with memory. Preprint at https://arxiv.org/abs/1606.08328 (2016).

  59. Borgatti, S. P. Centrality and network flow. Soc. Netw. 27, 55–71 (2005).

    Article  Google Scholar 

  60. Brandes, U., Heine, M., Müller, J. & Ortmann, M. Positional dominance: concepts and algorithms. In Conf. Algorithms and Discrete Applied Mathematics 60–71 (Springer, 2017).

  61. Freeman, L. A set of measures of centrality based on betweeneess. Sociometry 40, 35–41 (1977).

    Article  Google Scholar 

  62. de Bruijn, N. G. A combinatorial problem. Proc. K. Ned. Akad. Wet. 49, 758–764 (1946).

    MATH  Google Scholar 

  63. Zhang, Y., Garas, A. & Scholtes, I. Controllability of temporal networks: an analysis using higher-order networks. Preprint at https://arxiv.org/abs/1701.06331 (2017).

  64. Ciftcioglu, E. N., Ramanathan, R. & Basu, P. Generative models for global collaboration relationships. Sci. Rep. 7, 11160 (2017).

    Article  ADS  Google Scholar 

  65. 2013 Journal Citation Reports® (Thomson Reuters, 2013).

Download references

Acknowledgements

M.R. was supported by the Swedish Research Council, grant 2016-00796. I.S. acknowledges support by the Swiss National Science Foundation, grant 176938.

Author information

Authors and Affiliations

  1. Mathematical Institute, University of Oxford, Oxford, UK

    Renaud Lambiotte

  2. Integrated Science Lab, Department of Physics, Umeå University, Umeå, Sweden

    Martin Rosvall

  3. Data Analytics Group, Department of Informatics (IfI), University of Zurich, Zurich, Switzerland

    Ingo Scholtes

Authors
  1. Renaud Lambiotte
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martin Rosvall
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ingo Scholtes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ingo Scholtes.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Journal peer review information: Nature Physics thanks David Gleich and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lambiotte, R., Rosvall, M. & Scholtes, I. From networks to optimal higher-order models of complex systems. Nat. Phys. 15, 313–320 (2019). https://doi.org/10.1038/s41567-019-0459-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0459-y

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics