Abstract
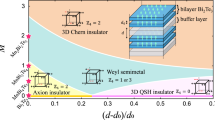
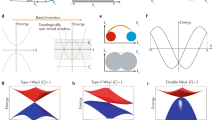
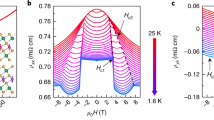
The existence of topological hinge states is a key signature for a newly proposed class of topological matter, the second-order topological insulators. In the present paper, a universal mechanism to generate chiral hinge states in the ferromagnetic axion insulator phase is introduced, which leads to an exotic transport phenomenon, the quantum anomalous Hall effect (QAHE) on some particular surfaces determined by both the crystalline symmetry and the magnetization direction. A realistic material system, Sm-doped Bi2Se3, is then proposed to realize such exotic hinge states by combining first-principles calculations and Green’s function techniques. A physically accessible way to manipulate the surface QAHE is also proposed, which makes it very different from the QAHE in ordinary 2D systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Ryu, S. et al. Topological origin of zero-energy edge states in particle–hole symmetric systems. Phys. Rev. Lett. 89, 077002 (2002).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Wang, Z. et al. Hourglass fermions. Nature 532, 189–194 (2016).
Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 71, 3697–3700 (1993).
Kane, C. L. et al. Z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Benalcazar, W. A. et al. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).
Langbehn, J. et al. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).
Ezawa, M. Magnetic second-order topological insulators and semimetals. Phys. Rev. B 97, 155305 (2018).
Schindler, Frank et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Benalcazar, W. A. et al. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Song, Z. et al. (d − 2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Schindler, F. et al. Higher-order topology in bismuth. Nat. Phys. 14, 918–924 (2018).
Fang, C. et al. Rotation anomaly and topological crystalline insulators. Preprint at https://arxiv.org/abs/1709.01929 (2017).
Ari, M. T. et al. Entanglement and inversion symmetry in topological insulators. Phys. Rev. B 82, 241102(R) (2012).
Taylor, L. H. et al. Inversion-symmetric topological insulators. Phys. Rev. B 83, 245132 (2011).
Eslam, K. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).
Zhida, S. et al. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 9, 3530 (2018).
Eslam, K. et al. Symmetry indicators and anomalous surface states of topological crystalline insulators. Phys. Rev. X 8, 031070 (2018).
Xiaoting, Z. et al. Topological crystalline insulator states in the Ca2As family. Phys. Rev. B 98, 241104 (2018).
Hassan, S. et al. Topological crystalline superconductivity and second-order topological superconductivity in nodal-loop materials. Phys. Rev. B 97, 094508 (2018).
Yizhi, Y. et al. Higher order symmetry-protected topological states for interacting bosons and fermions. Phys. Rev. B 98, 235102 (2018).
Sheng-Jie, H. et al. Building crystalline topological phases from lower-dimensional states. Phy. Rev. B 96, 205106 (2017).
Hasan, M. Z. et al. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. et al. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Yoichi, A. et al. Topological crystalline insulators and topological superconductors: from concepts to materials. Ann. Rev. Cond. Mat. Phys. 6, 361–381 (2015).
Po, H. C. et al. Complete theory of symmetry-based indicators of band topology. Nat. Commun. 8, 50 (2017).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
Soluyanov, A. A. et al. Wannier representation of topological insulators. Phys. Rev. B 83, 035108 (2011).
Klitzing, K. V. et al. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Mong, R. S. K. et al. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Nomura, K. et al. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Haldane, F. D. M. Model for a quantum hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett 61, 2015–2018 (1988).
Liang, Wu et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3d topological insulator. Science 354, 1124–1127 (2016).
Luka, T. et al. Higher-order bulk-boundary correspondence for topological crystalline phases. Phys. Rev. X 9, 011012 (2019).
Chen, T. et al. High-mobility Sm-doped Bi2Se3 ferromagnetic topological insulators and robust exchange coupling. Adv. Mater. 27, 4819–4823 (2015).
Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 58, 1799–1802 (1987).
Qi, X.-L. et al. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Essin, A. M. et al. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Ari, M. T. et al. Quantized response and topology of magnetic insulators with inversion symmetry. Phys. Rev. B 85, 165120 (2012).
Zhang, F. et al. Surface state magnetization and chiral edge states on topological insulators. Phys. Rev. Lett. 110, 046404 (2013).
Sancho., M. P. L. et al. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F 15, 851 (1985).
Zhi, R. et al. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010).
Chen, Y. L. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Kresse, G. et al. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. et al. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci 6, 15–50 (1996).
Kresse, G. et al. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Arash, A. M. et al. An updated version of wannier90: a tool for obtaining maximally-localized Wannier functions. Com. Phys. Comm. 185, 2309–2310 (2014).
Acknowledgements
We thank B.A. Bernevig and T. Neupert for helpful discussions. X.D., C.F. and H.M.W. are supported by the Ministry of Science and Technology of China (grant no. 2016YFA0300600) and the K.C. Wong Education Foundation (grant no. GJTD-2018-01). X.D. acknowledges financial support from the Hong Kong Research Grants Council (project no. GRF16300918). C.F. acknowledges financial support from the Ministry of Science and Technology of China (grant no. 2016YFA0302400), the Natural Science Foundation of China (grant no. 11674370), the Chinese Academy of Sciences (no. XXH13506-202, XDB28000000), the Beijing Municipal Science & Technology Commission (no. Z181100004218001) and the Beijing Natural Science Foundation (no. Z180008). H.M.W. is also supported by the Ministry of Science and Technology of China (grant no. 2018YFA0305700), the National Natural Science Foundation (grant no. 11674369) and the Science Challenge Project (no. TZ2016004). Y.-M.L. acknowledges the NSF under award number DMR-1653769.
Author information
Authors and Affiliations
Contributions
C.F., Y.M.L. and X.D. developed the theory and designed the research. C.M.Y. carried out the numerical calculations for the hinge states. Y.F.X. and H.M.W. did the calculations for the effective exchange field. Z.D.S. did the symmetry analyses for the numerical results. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Minoru Kawamura, Titus Neupert and other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Appendices and Supplementary Figures 1–4
Rights and permissions
About this article
Cite this article
Yue, C., Xu, Y., Song, Z. et al. Symmetry-enforced chiral hinge states and surface quantum anomalous Hall effect in the magnetic axion insulator Bi2–xSmxSe3. Nat. Phys. 15, 577–581 (2019). https://doi.org/10.1038/s41567-019-0457-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0457-0
This article is cited by
-
The higher-order topological pumping explored in the 2D acoustic crystal
Science China Physics, Mechanics & Astronomy (2024)
-
Topological electronic structure and spin texture of quasi-one-dimensional higher-order topological insulator Bi4Br4
Nature Communications (2023)
-
Anisotropic transport in a possible quasi-one-dimensional topological candidate: TaNi2Te3
Tungsten (2023)
-
Third-order topological insulators with wallpaper fermions in Tl4PbTe3 and Tl4SnTe3
npj Computational Materials (2022)
-
Quadrupole topological insulators in Ta2M3Te5 (M = Ni, Pd) monolayers
npj Quantum Materials (2022)