Abstract
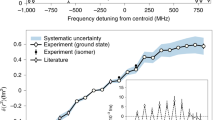
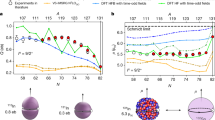
One of the most important global properties of the atomic nucleus is its size. Experimentally determined nuclear charge radii carry unique information on the nuclear force and complex dynamics of protons and neutrons moving inside the nucleus. The intricate behaviour of charge radii along the chain of Ca isotopes, including the unexpectedly large charge radius of neutron-rich 52Ca, poses a daunting challenge for nuclear theory1. Here we present the measurements of the charge radii of proton-rich isotopes 36,37,38Ca, whose properties are impacted by the interplay between nuclear superfluidity and weak binding. Calculations carried out within nuclear density functional theory show that the combination of a novel interaction2 and a state-of-the-art theoretical method can successfully explain the behaviour of charge radii from the lightest to the heaviest Ca isotopes. Through this model, we show how the new data on 36,37,38Ca elucidate the nature of nucleonic pairing in weakly bound proton-rich isotopes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Garcia Ruiz, R. F. et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat. Phys. 12, 594–598 (2016).
Fayans, S. A. Towards a universal nuclear density functional. JETP Lett. 68, 169–174 (1998).
Bohr, A., Mottelson, B. R. & Pines, D. Possible analogy between the excitation spectra of nuclei and those of the superconducting metallic state. Phys. Rev. 110, 936–938 (1958).
Brink, D. M. & Broglia, R. A. Nuclear Superfluidity, Pairing in Finite Systems (Cambridge Univ. Press, Cambridge, 2005).
Broglia, R. A. & Zelevinski, V. (eds.) 50 Years of Nuclear BCS (World Scientific, Singapore, 2012).
Dean, D. J. & Hjorth-Jensen, M. Pairing in nuclear systems: from neutron stars to finite nuclei. Rev. Mod. Phys. 75, 607–656 (2003).
Dobaczewski, J., Nazarewicz, W. & Reinhard, P.-G. Pairing interaction and self-consistent densities in neutron-rich nuclei. Nucl. Phys. A. 693, 361–373 (2001).
Jensen, A. S., Riisager, K., Fedorov, D. V. & Garrido, E. Structure and reactions of quantum halos. Rev. Mod. Phys. 76, 215–261 (2004).
Pfützner, M., Karny, M., Grigorenko, L. V. & Riisager, K. Radioactive decays at limits of nuclear stability. Rev. Mod. Phys. 84, 567–619 (2012).
Agrawal, B. K., Sil, T., Samaddar, S. K., De, J. N. & Shlomo, S. Coulomb energy differences in mirror nuclei revisited. Phys. Rev. C 64, 024305 (2001).
Caurier, E., Langanke, K., Martínez-Pinedo, G., Nowacki, F. & Vogel, P. Shell model description of isotope shifts in calcium. Phys. Lett. B 522, 240–244 (2001).
Minamisono, K. et al. Charge radii of neutron deficient 52,53Fe produced by projectile fragmentation. Phys. Rev. Lett. 117, 252501 (2016).
Reinhard, P.-G. & Nazarewicz, W. Toward a global description of nuclear charge radii: exploring the Fayans energy density functional. Phys. Rev. C 95, 064328 (2017).
Vermeeren, L. et al. The mean square nuclear charge radius of 39Ca. J. Phys. G 22, 1517–1520 (1996).
Morrissey, D. J., Sherrill, B. M., Steiner, M., Stolz, A. & Wiedenhoever, I. Commissioning the A1900 projectile fragment separator. Nucl. Instrum. Methods Phys. Res. B 204, 90–96 (2003).
Cooper, K. et al. Extraction of thermalized projectile fragments from a large volume gas cell. Nucl. Instrum. Methods Phys. Res. A 763, 543–546 (2014).
Trinder, W. et al. Study of the β decays of 37Ca and 36Ca. Nucl. Phys. A. 620, 191–213 (1997).
Campbell, P., Moore, I. D. & Pearson, M. R. Laser spectroscopy for nuclear structure physics. Prog. Part. Nucl. Phys. 86, 127–180 (2016).
Neugart, R. et al. Collinear laser spectroscopy at ISOLDE: new methods and highlights. J. Phys. G 44, 064002 (2017).
Hick, A. et al. Beta decay of the new isotopes 52K, 52Ca and 52Sc; a test of the shell model far from stability. Phys. Rev. C 31, 2226–2237 (1985).
Minamisono, K. et al. Commissioning of the collinear laser spectroscopy system in the BECOLA facility at NSCL. Nucl. Instrum. Methods Phys. Res. A 709, 85–94 (2013).
Rossi, D. M. et al. A field programmable gate array-based time-resolved scaler for collinear laser spectroscopy with bunched radioactive potassium beams. Rev. Sci. Instrum. 85, 093503 (2014).
Barquest, B. R. et al. RFQ beam cooler and buncher for collinear laser spectroscopy of rare isotopes. Nucl. Instrum. Methods Phys. Res. A 866, 18–28 (2017).
Nieminen, A. et al. On-line ion cooling and bunching for collinear laser spectroscopy. Phys. Rev. Lett. 88, 094801 (2002).
Campbell, P. et al. Laser spectroscopy of cooled zirconium fission fragments. Phys. Rev. Lett. 89, 082501 (2002).
Shi, C. et al. Unexpectedly large difference of the electron density at the nucleus in the 4p 2P1/2,3/2 fine-structure doublet of Ca+. Appl. Phys. B 123, 2 (2016).
Klein, A. et al. Moments and mean square charge radii of short-lived argon isotopes. Nucl. Phys. A 607, 1–22 (1996).
Rossi, D. M. et al. Charge radii of neutron-deficient 36K and 37K. Phys. Rev. C 92, 014305 (2015).
Dobaczewski, J. et al. Mean-field description of ground-state properties of drip-line nuclei: Pairing and continuum effects. Phys. Rev. C 53, 2809–2840 (1996).
Bender, M., Heenen, P.-H. & Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 75, 121–180 (2003).
Klüpfel, P., Reinhard, P.-G., Bürvenich, T. J. & Maruhn, J. A. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters. Phys. Rev. C 79, 034310 (2009).
Fayans, S. A., Tolokonnikov, S. V., Trykov, E. L. & Zawischa, D. Nuclear isotope shifts within the local energy-density functional approach. Nucl. Phys. A 676, 49–119 (2000).
Dobaczewski, J., Flocard, H. & Treiner, J. Hartree–Fock–Bogolyubov description of nuclei near the neutron-drip line. Nucl. Phys. A 422, 103–139 (1984).
Hammen, M. et al. From calcium to cadmium: testing the pairing functional through charge radii measurements of 100−130Cd. Phys. Rev. Lett. 121, 102501 (2018).
Fricke, G. & Heilig, K. Nuclear Charge Radii (Springer, Berlin, 2004).
Äystö, J. Development and applications of the IGISOL technique. Nucl. Phys. A 693, 477–497 (2001).
Brockton Electro-Optics Corp. Take Control of Your Laser! http://www.brocktoneo.com (accessed in 2016).
Ryder, C. A. et al. Population distribution subsequent to charge exchange of 29.85 keV Ni+ on sodium vapor. Spectrochim. Acta B 113, 16–21 (2015).
Stancik, A. L. & Brauns, E. B. A simple asymmetric lineshape for fitting infrared absorption spectra. Vib. Spectrosc. 47, 66–69 (2008).
Reinhard, P.-G., Bender, M., Rutz, K. & Maruhn, J. An HFB scheme in natural orbitals. Z. Phys. A 358, 277–278 (1997).
Erler, J., Klüpfel, P. & Reinhard, P.-G. A stabilized pairing functional. Eur. Phys. J. A 37, 81–86 (2008).
Hinohara, N. & Nazarewicz, W. Pairing Nambu–Goldstone modes within nuclear density functional theory. Phys. Rev. Lett. 116, 152502 (2016).
Duguet, T., Bonche, P., Heenen, P.-H. & Meyer, J. Pairing correlations. I. description of odd nuclei in mean-field theories. Phys. Rev. C 65, 014310 (2001).
Schunck, N. et al. One-quasiparticle states in the nuclear energy density functional theory. Phys. Rev. C 81, 024316 (2010).
Tolokonnikov, S. V. & Saperstein, E. E. Description of superheavy nuclei on the basis of a modified version of the DF3 energy functional. Phys. At. Nucl. 73, 1684–1699 (2010).
Saperstein, E. E. & Tolokonnikov, S. V. Self-consistent theory of finite Fermi systems and radii of nuclei. Phys. At. Nucl. 74, 1277–1298 (2011).
Brown, B. A. Mirror charge radii and the neutron equation of state. Phys. Rev. Lett. 119, 122502 (2017).
Acknowledgements
This work was supported in part by the National Science Foundation, Grant No. PHY-15-65546; the US Department of Energy, National Nuclear Security Administration, Grant No. DE-NA0002924; the US Department of Energy, Office of Science, Office of Nuclear Physics, Grant Nos. DE-SC0013365, DE-SC0018083 and DE-AC05-00OR22725 with UT-Battelle, LLC; the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 279384907 – SFB 1245; and the German Federal Ministry of Education and Research (BMBF), Grant No. 05P12RFFTG.
Author information
Authors and Affiliations
Contributions
A.J.M., K.M., A.K., D.G., J.D.L., Y.L., P.F.M., S.V.P., D.M.R., F.S., C.S. and A.T. performed the experiment. A.J.M., C.K., B.M., W. Nörtershäuser and J.W. designed and installed the upgraded photon detection system. A.J.M. performed data analysis and discussed with K.M., A.K., W. Nörtershäuser and D.M.R. W. Nazarewicz and P.-G.R. performed theoretical analysis. A.J.M., K.M., W. Nazarewicz and P.-G.R. prepared the figures. A.J.M., K.M., W. Nazarewicz and P.-G.R. prepared the manuscript. All authors discussed the results and contributed to the manuscript at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Miller, A.J., Minamisono, K., Klose, A. et al. Proton superfluidity and charge radii in proton-rich calcium isotopes. Nat. Phys. 15, 432–436 (2019). https://doi.org/10.1038/s41567-019-0416-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0416-9
This article is cited by
-
Nuclear charge radius predictions by kernel ridge regression with odd–even effects
Nuclear Science and Techniques (2024)
-
Constraining nuclear symmetry energy with the charge radii of mirror-pair nuclei
Nuclear Science and Techniques (2023)
-
A combined Glauber model plus relativistic Hartree–Bogoliubov theory analysis of nuclear reactions with light and medium mass nuclei
Pramana (2022)
-
Commissioning of a high-resolution collinear laser spectroscopy apparatus with a laser ablation ion source
Nuclear Science and Techniques (2022)
-
Charge radii of exotic potassium isotopes challenge nuclear theory and the magic character of N = 32
Nature Physics (2021)