Abstract
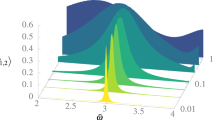
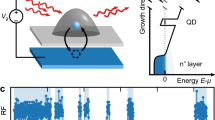
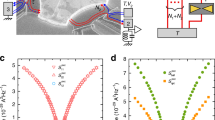
In stochastic resonance, the combination of a weak signal with noise leads to its amplification and optimization1. This phenomenon has been observed in several systems in contexts ranging from palaeoclimatology, biology, medicine, sociology and economics to physics1,2,3,4,5,6,7,8,9. In all these cases, the systems were either operating in the presence of thermal noise or were exposed to external classical noise sources. For quantum-mechanical systems, it has been theoretically predicted that intrinsic fluctuations lead to stochastic resonance as well, a phenomenon referred to as quantum stochastic resonance1,10,11, but this has not been reported experimentally so far. Here we demonstrate tunnelling-controlled quantum stochastic resonance in the a.c.-driven charging and discharging of single electrons on a quantum dot. By analysing the counting statistics12,13,14,15,16, we demonstrate that synchronization between the sequential tunnelling processes and a periodic driving signal passes through an optimum, irrespective of whether the external frequency or the internal tunnel coupling is tuned.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon request.
References
Gammaitoni, L., Hänggi, P., Jung, P. & Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 70, 223–288 (1998).
Lee, I. Y., Liu, X. L., Kosko, B. & Zhou, C. W. Nanosignal processing: stochastic resonance in carbon nanotubes that detect subthreshold signals. Nano Lett. 3, 1683–1686 (2003).
Badzey, R. L. & Mohanty, P. Coherent signal amplification in bistable nanomechanical oscillators by stochastic resonance. Nature 437, 995–998 (2005).
Nishiguchi, K. & Fujiwara, A. Detecting signals buried in noise via nanowire transistors using stochastic resonance. Appl. Phys. Lett. 101, 193108 (2012).
Venstra, W. J., Westra, H. J. R. & van der Zant, H. S. J. Stochastic switching of cantilever motion. Nat. Commun. 4, 2624 (2013).
Abbaspour, H., Trebaol, S., Morier-Genoud, F., Portella-Oberli, M. T. & Deveaud, B. Stochastic resonance in collective exciton–polariton excitations inside a GaAs microcavity. Phys. Rev. Lett. 113, 057401 (2014).
Sun, G. et al. Detection of small single-cycle signals by stochastic resonance using a bistable superconducting quantum interference devices. Appl. Phys. Lett. 106, 172602 (2015).
Stroescu, I., Hume, D. B. & Oberthaler, M. K. Dissipative double-well potential for cold atoms: kramers rate and stochastic resonance. Phys. Rev. Lett. 117, 243005 (2016).
Monifi, F. et al. Optomechanically induced stochastic resonance and chaos transfer between optical fields. Nat. Photon. 10, 399–405 (2016).
Löfstedt, R. & Coppersmith, S. N. Quantum stochastic resonance. Phys. Rev. Lett. 72, 1947–1950 (1994).
Grifoni, M. & Hänggi, P. Coherent and incoherent quantum stochastic resonance. Phys. Rev. Lett. 76, 1611–1614 (1996).
Callenbach, L., Hänggi, P., Linz, S. J., Freund, J. A. & Schimansky-Geier, L. Oscillatory systems driven by noise: frequency and phase synchronization. Phys. Rev. E 65, 051110 (2002).
Talkner, P. Statistics of entrance times. Physica A 325, 124–135 (2003).
Talkner, P., Machura, Ł., Schindler, M., Hänggi, P. & Łuczka, J. Statistics of transition times, phase diffusion and synchronization in periodically driven bistable systems. New J. Phys. 7, 14 (2005).
Gustavsson, S. et al. Counting statistics of single-electron transport in a quantum dot. Phys. Rev. Lett. 96, 076605 (2006).
Wagner, T. et al. Strong suppression of shot noise in a feedback-controlled single-electron transistor. Nat. Nanotechnol. 12, 218–222 (2017).
Kouwenhoven, L. P., Austing, D. G. & Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 64, 701–736 (2001).
Kouwenhoven, L. P., Johnson, A. T., van der Vaart, N. C., Harmans, C. J. P. M. & Foxon, C. T. Quantized current in a quantum-dot turnstile using oscillating tunnel barriers. Phys. Rev. Lett. 67, 1626–1629 (1991).
Platonov, S. et al. Lissajous rocking ratchet: realization in a semiconductor quantum dot. Phys. Rev. Lett. 115, 106801 (2015).
Blumenthal, M. D. et al. Gigahertz quantized charge pumping. Nat. Phys. 3, 343–347 (2007).
Pekola, J. P. et al. Single-electron current sources: toward a refined definition of the ampere. Rev. Mod. Phys. 85, 1421–1472 (2013).
Shulgin, B., Neiman, A. & Anishchenko, V. Mean switching frequency locking in stochastic bistable systems driven by a periodic force. Phys. Rev. Lett. 75, 4157–4160 (1995).
Burk, H., de Jong, M. J. M. & Schönberger, C. Shot-noise in the single-electron regime. Phys. Rev. Lett. 75, 1610–1613 (1995).
Pekola, J. P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 11, 118–123 (2015).
Féve, G. et al. An on-demand coherent single-electron source. Science 316, 1169–1172 (2007).
Albert, M., Flindt, C. & Büttiker, M. Distributions of waiting times of dynamic single-electron emitters. Phys. Rev. Lett. 107, 086805 (2011).
Mozyrsky, D., Martin, I. & Hastings, M. B. Quantum-limited sensitivity of single-electron-transistor-based displacement detectors. Phys. Rev. Lett. 92, 018303 (2004).
LaHaye, M. D., Buu, O., Camarota, B. & Schwab, K. C. Approaching the quantum limit of a nanomechanical resonator. Science 304, 74–77 (2004).
Bonet, E., Deshmukh, M. M. & Ralph, D. C. Solving rate equations for electron tunneling via discrete quantum states. Phys. Rev. B 65, 045317 (2002).
Hofmann, A. et al. Measuring the degeneracy of discrete energy levels using a GaAs/AlGaAs quantum dot. Phys. Rev. Lett. 117, 206803 (2017).
Acknowledgements
This work was supported financially by the Research Training Group 1991 (DFG), the School for Contacts in Nanosystems (NTH), the Center for Quantum Engineering and Space-Time Research (QUEST), the Laboratory for Nano and Quantum Engineering (LNQE) and the ‘Fundamentals of Physics and Metrology’ initiative (T.W, J.C.B., E.R. and R.J.H.).
Author information
Authors and Affiliations
Contributions
T.W. carried out the experiments, analysed the data and wrote the manuscript. J.C.B. and T.W. fabricated the device. E.P.R. grew the wafer material. P.T. and P.H. provided theory support. T.W., P.T., P.H. and R.J.H discussed the results. R.J.H. supervised the research. All authors contributed to editing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Christian Flindt and the other anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures and Methods
Rights and permissions
About this article
Cite this article
Wagner, T., Talkner, P., Bayer, J.C. et al. Quantum stochastic resonance in an a.c.-driven single-electron quantum dot. Nat. Phys. 15, 330–334 (2019). https://doi.org/10.1038/s41567-018-0412-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0412-5
This article is cited by
-
Stochastic resonance of spinor condensates in optical cavity
Science China Physics, Mechanics & Astronomy (2024)
-
Stochastic resonance in strong Poisson white noise excited system and its application in multi-features identification
Pramana (2024)
-
Post-processing of real-time quantum event measurements for an optimal bandwidth
Scientific Reports (2023)
-
Stochastic resonance in image denoising as an alternative to traditional methods and deep learning
Nonlinear Dynamics (2022)
-
Stochastic Resonance in a Fractional Oscillator with Cross-Correlation Noise
Journal of Statistical Physics (2022)