Abstract
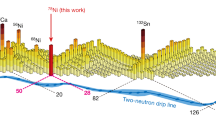
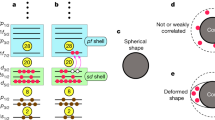
Exotic nuclei are characterized by having a number of neutrons (or protons) in excess relative to stable nuclei. Their shell structure, which represents single-particle motion in a nucleus1,2, may vary due to nuclear force and excess neutrons3,4,5,6, in a phenomenon called shell evolution7. This effect could be counterbalanced by collective modes causing deformations of the nuclear surface8. Here, we study the interplay between shell evolution and shape deformation by focusing on the magnetic moment of an isomeric state of the neutron-rich nucleus 75Cu. We measure the magnetic moment using highly spin-controlled rare-isotope beams and achieve large spin alignment via a two-step reaction scheme9 that incorporates an angular-momentum-selecting nucleon removal. By combining our experiments with numerical simulations of many-fermion correlations, we find that the low-lying states in 75Cu are, to a large extent, of single-particle nature on top of a correlated 74Ni core. We elucidate the crucial role of shell evolution even in the presence of the collective mode, and within the same framework we consider whether and how the double magicity of the 78Ni nucleus is restored, which is also of keen interest from the perspective of nucleosynthesis in explosive stellar processes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data used in the present study are available from the corresponding author upon reasonable request.
References
Mayer, M. G. et al. On closed shells in nuclei. II. Phys. Rev. 75, 1969–1970 (1949).
Haxel, O., Jensen, J. H. D. & Suess, H. E. On the ‘magic numbers’ in nuclear structure. Phys. Rev. 75, 1766–1766 (1949).
Warner, D. Not-so-magic numbers. Nature 430, 517–519 (2004).
Janssens, R. V. F. et al. Unexpected doubly magic nucleus. Nature 459, 1069–1070 (2009).
Bastin, B. et al. Collapse of the N = 28 shell closure in 42Si. Phys. Rev. Lett. 99, 022503 (2007).
Steppenbeck, D. et al. Evidence for a new nuclear ‘magic number’ from the level structure of 54Ca. Nature 502, 207–210 (2013).
Otsuka, T. et al. Evolution of nuclear shells due to the tensor force. Phys. Rev. Lett. 95, 232502 (2005).
Bohr, A. & Mottelson, B. R. Nuclear Structure (Benjamin, New York, 1969).
Ichikawa, Y. et al. Production of spin-controlled rare isotope beams. Nat. Phys. 8, 918–922 (2012).
Franchoo, S. et al. Beta decay of 68–74Ni and level structure of neutron-rich Cu isotopes. Phys. Rev. Lett. 81, 3100–3103 (1998).
Flanagan, K. T. et al. Nuclear spins and magnetic moments of 71,73,75Cu: inversion of π2p 3/2 and π1f 5/2 levels in 75Cu. Phys. Rev. Lett. 103, 142501 (2009).
Otsuka, T. et al. Novel features of nuclear forces and shell evolution in exotic nuclei. Phys. Rev. Lett. 104, 012501 (2010).
Petrone, C. et al. Nearly degenerate isomeric states of 75Cu. Phys. Rev. C 94, 024319 (2016).
Asahi, K. et al. New aspect of intermediate energy heavy ion reactions. large spin polarization of fragments. Phys. Lett. B 251, 488–492 (1990).
Kubo, T. In-flight RI beam separator BigRIPS at RIKEN and elsewhere in Japan. Nucl. Instrum. Meth. B 204, 97–113 (2003).
Yano, Y. The RIKEN RI beam factory project: a status report. Nucl. Instrum. Meth. B 261, 1009–1013 (2007).
Hüfner, J. & Nemes, M. C. Relativistic heavy ions measure the momentum distribution on the nuclear surface. Phys. Rev. C 23, 2538–2547 (1981).
Talmi, I. Simple Models of Complex Nuclei (CRC Press, Boca Raton, 1990).
Shimizu, N. et al. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 01A205 (2012).
Otsuka, T. et al. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 47, 319–400 (2001).
Tsunoda, Y. et al. Novel shape evolution in exotic Ni isotopes and configuration-dependent shell structure. Phys. Rev. C 89, 031301(R) (2014).
Otsuka, T. & Tsunoda, Y. The role of shell evolution in shape coexistence. J. Phys. G. Nucl. Part. Phys. 43, 024009 (2016).
Olivier, L. et al. Persistence of the Z = 28 shell gap around 78Ni: first spectroscopy of 79Cu. Phys. Rev. Lett. 119, 192501 (2017).
Welker, A. et al. Binding energy of 79Cu: probing the structure of the doubly magic 78Ni from only one proton away. Phys. Rev. Lett. 119, 192502 (2017).
Hagen, G., Jansen, G. R. & Papenbrock, T. Structure of 78Ni from first-principles computations. Phys. Rev. Lett. 117, 172501 (2016).
Nowacki, F., Poves, A., Caurier, E. & Bounthong, B. Shape coexistence in 78Ni as the portal to the fifth island of inversion. Phys. Rev. Lett. 117, 272501 (2016).
Sullivan, C. et al. The sensitivity of core-collapse supernovae to nuclear electron capture. Astrophys. J. 816, 44 (2016).
Köster, U. et al. In-source laser spectroscopy of 75,77,78Cu: direct evidence for a change in the quasiparticle energy sequence in 75,77Cu and an absence of longer-lived isomers in 78Cu. Phys. Rev. C 84, 034320 (2011).
Sahin, E. et al. Shell evolution towards 78Ni: low-lying states in 77Cu. Phys. Rev. Lett. 118, 242502 (2017).
Stone, N. J. et al. Nuclear dipole moment of 71Cu from online β-NMR measurements. Phys. Rev. C 77, 014315 (2008).
Goldhaber, A. S. Statistical models of fragmentation processes. Phys. Lett. B 53, 306–308 (1974).
Morinaga, H. & Yamazaki, T. In-Beam Gamma-Ray Spectroscopy (North-Holland, Amsterdam, 1976).
de Groote, R. P. et al. Dipole quadrupole moments of 73–78Cu as a test of the robustness of the Z = 28 shell closure near 78Ni. Phys. Rev. C 96, 041302(R) (2017).
Wraith, C. et al. Evolution of nuclear structure in neutron-rich odd-Zn isotopes and isomers. Phys. Lett. B 771, 385–391 (2017).
Castel, B. & Towner, I. S. Modern Theories of Nuclear Moments (Clarendon Press, New York, 1990).
Towner, I. S. Quenching of spin matrix elements in nuclei. Phys. Rep. 155, 263–377 (1987).
Honma, M., Otsuka, T., Brown, B. A. & Hjorth-Jensen, M. New effective interaction for f 5 pg 9-shell nuclei. Phys. Rev. C 80, 064323 (2009).
Caurier, E. et al. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 77, 427–488 (2005).
Honma, M., Otsuka, T., Brown, B. A. & Mizusaki, T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys. Rev. C 69, 034335 (2004).
Stefanescu, I. et al. Interplay between single-particle and collective effects in the odd-A Cu isotopes beyond N = 40. Phys. Rev. Lett. 100, 112502 (2008).
Acknowledgements
The experiment was performed under programme no. NP1412-RIBF124R1 at RIBF, operated by RIKEN Nishina Center for Accelerator-Based Science and CNS, The University of Tokyo. The authors thank the RIKEN accelerator staff for their cooperation during the experiment. This work was supported in part by a JSPS KAKENHI grant (16K05390), and also in part by JSPS and CNRS under the Japan-France Research Cooperative Program. The MCSM calculations were performed on the K computer at RIKEN AICS (hp140210, hp150224, hp160211, hp170230). This work was also supported in part by the HPCI Strategic Program (‘The Origin of Matter and the Universe’) and ‘Priority Issue on Post-K computer’ (Elucidation of the Fundamental Laws and Evolution of the Universe). D.L.B., and A.K. acknowledge support by the Extreme Light Infrastructure Nuclear Physics (ELI-NP) Phase II, a project co-financed by the Romanian Government and the European Union through the European Regional Development Fund – the Competitiveness Operational Programme(1/07.07.2016, COP, ID 1334). D.R. was supported by the P2IO Excellence Center.
Author information
Authors and Affiliations
Contributions
Y.I. designed the experiment, analysed the data and was chiefly responsible for writing the paper. Y.T. and T.O. worked on the theoretical studies, and T.O. helped with writing the paper. The other authors are collaborators on the experiment.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Thomas Papenbrock and other anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ichikawa, Y., Nishibata, H., Tsunoda, Y. et al. Interplay between nuclear shell evolution and shape deformation revealed by the magnetic moment of 75Cu. Nat. Phys. 15, 321–325 (2019). https://doi.org/10.1038/s41567-018-0410-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0410-7
This article is cited by
-
Nuclear-moment measurement using highly spin-aligned RI beams: Recent activities at RIBF
Interactions (2024)
-
α-Clustering in atomic nuclei from first principles with statistical learning and the Hoyle state character
Nature Communications (2022)
-
The impact of nuclear shape on the emergence of the neutron dripline
Nature (2020)