Abstract
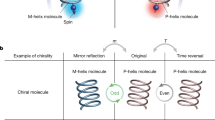
According to quantum mechanics, chiral states cannot be non-degenerate eingenstates of a parity-conserving Hamiltonian. This is in contradiction to the existence of chiral molecules—a fact known as as the Hund paradox1. The origin of molecular and biological chirality is conjectured to be related to parity-breaking interactions2,3 or environmental decoherence4, but a quantum superposition of two chiral molecular states with distinctive optical activities has never been observed5. To make progress in addressing these questions, it would be helpful to construct an artificial quantum system that breaks the parity symmetry and that can be prepared in a superposition of two chiral states. Here we report the synthesis of the parity-breaking antisymmetric spin exchange interaction in all-to-all connected superconducting circuits, which allows us to show various chiral spin dynamics in up to five-spin clusters. We also demonstrate the entanglement of up to five qubits in Greenberger–Horne–Zeilinger states based on a three-spin chiral logic gate. Our results are a step towards quantum simulation of magnetism with antisymmetric spin exhange interaction and quantum computation with chiral spin states.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Hund, F. Zur Deutung der Molekelspektren III. Z. Physik 43, 805–826 (1927).
Mason, S. F. Origins of biomolecular handedness. Nature 311, 19–23 (1984).
Darquie, B. et al. Progress toward the first observation of parity violation in chiral molecules by high-resolution laser spectroscopy. Chirality 22, 870–884 (2010).
Trost, J. & Hornberger, K. Hund’s paradox and the collisional stabilization of chiral molecules. Phys. Rev. Lett. 103, 023202 (2009).
Cina, J. A. & Harris, R. A. Superpositions of handed wave functions. Science 267, 832–833 (1995).
Houck, A. A., Tureci, H. E. & Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 8, 292–299 (2012).
Xiang, Z.-L., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653 (2013).
Roushan, P. et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 13, 146–151 (2017).
Roushan, P. et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science 358, 1175–1179 (2017).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Wang, D.-W., Cai, H., Liu, R.-B. & Scully, M. O. Mesoscopic superposition states generated by synthetic spin–orbit interaction in Fock-state lattices. Phys. Rev. Lett. 116, 220502 (2016).
Dzialoshinskii, I. E. Thermodynamic theory of weak ferromagnetism in antiferromagnetic substances. J. Exp. Theoret. Phys. 32, 1547–1562 (1957).
Moriya, T. New mechanism of anisotropic superexchange interaction. Phys. Rev. Lett. 4, 228–230 (1960).
Ma, X. et al. Dzyaloshinskii–Moriya interaction across an antiferromagnet–ferromagnet interface. Phys. Rev. Lett. 119, 027202 (2017).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Dmitrienko, V. E. et al. Measuring the Dzyaloshinskii–Moriya interaction in a weak ferromagnet. Nat. Phys. 10, 202–206 (2014).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Takagi, R. et al. Spin-wave spectroscopy of the Dzyaloshinskii–Moriya interaction in room-temperature chiral magnets hosting skyrmions. Phys. Rev. B 95, 220406 (2017).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Wen, X. G., Wilczek, F. & Zee, A. Chiral spin states and superconductivity. Phys. Rev. B 39, 11413–11423 (1989).
Grohol, D. et al. Spin chirality on a two-dimensional frustrated lattice. Nat. Mater. 4, 323–328 (2005).
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N. & Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 291, 2573–2576 (2001).
Trif, M., Troiani, F., Stepanenko, D. & Loss, D. Spin–electric coupling in molecular magnets. Phys. Rev. Lett. 101, 217201 (2008).
Christandl, M., Datta, N., Ekert, A. & Landahl, A. J. Perfect state transfer in quantum spin networks. Phys. Rev. Lett. 92, 187902 (2004).
Eldredge, Z. et al. Fast quantum state transfer and entanglement renormalization using long-range interactions. Phys. Rev. Lett. 119, 170503 (2017).
Georgeot, B. & Mila, F. Chirality of triangular antiferromagnetic clusters as a qubit. Phys. Rev. Lett. 104, 200502 (2010).
Scarola, V. W., Park, K. & Sarma, S. D. Chirality in quantum computation with spin cluster qubits. Phys. Rev. Lett. 93, 120503 (2004).
Scully, M. O. Single photon subradiance: quantum control of spontaneous emission and ultrafast readout. Phys. Rev. Lett. 115, 243602 (2015).
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244 (2009).
Song, C. et al. 10-qubit entanglement and parallel logic operations with a superconducting circuit. Phys. Rev. Lett. 119, 180511 (2017).
Kyriienko, O. & Sorensen, A. S. Floquet quantum simulation with superconducting qubits. Phys. Rev. Appl. 9, 064029 (2018).
Wu, Y. et al. An efficient and compact switch for quantum circuits. npj Quantum Inf. 4, 50 (2018).
Koch, J., Houck, A. A., Hur, K. L. & Girvin, S. M. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 82, 043811 (2010).
Otfried, G. & Seevinck, M. Separability criteria for genuine multiparticle entanglement. New J. Phys. 12, 053002 (2010).
Acknowledgements
The authors thank W. Liu, Q. Guo and K. Huang for technical support. This research was supported by the National Key Research and Development Program of China (grants nos. 2018YFA0307200, 2017YFA0304202 and 2016YFA0300601), the National Natural Science Foundations of China (grants nos. 11434008, 11574380, 11725419 and 11874322) and the Fundamental Research Funds for the Central Universities of China (grant no. 2016XZZX002-01). D.W.W. was also supported by the key research programme of the Chinese Academy of Sciences (grant no. XDPB08-3). M.O.S. was supported by the Air Force Office of Scientific Research (award no. FA9550-18-1-0141), the Office of Naval Research (award no. N00014-16-1-3054) and the Robert A. Welch Foundation (grant no. A-1261). Devices were made at the Nanofabrication Facilities at the Institute of Physics in Beijing, the University of Science and Technology of China in Hefei and the National Center for Nanoscience and Technology in Beijing.
Author information
Authors and Affiliations
Contributions
D.W.W. conceived the idea and formulated the theory. D.W.W. and H.W. planned the project. C.S. performed the experiments. W.F., H.C. and C.S. carried out the simulation and analysed the data. H.D., H.L., D.Z. and X.Z. fabricated the sample with designs and support from H.W.’s group. D.X. provided technical support. D.W.W., W.F. and H.W. wrote the paper and S.Y.Z. and M.O.S. made comments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary methods and figures
Rights and permissions
About this article
Cite this article
Wang, DW., Song, C., Feng, W. et al. Synthesis of antisymmetric spin exchange interaction and chiral spin clusters in superconducting circuits. Nat. Phys. 15, 382–386 (2019). https://doi.org/10.1038/s41567-018-0400-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0400-9
This article is cited by
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Quantum simulation of Hofstadter butterfly with synthetic gauge fields on two-dimensional superconducting-qubit lattices
Frontiers of Physics (2023)
-
Experimental realization of phase-controlled dynamics with hybrid digital–analog approach
npj Quantum Information (2021)
-
Topological characterizations of an extended Su–Schrieffer–Heeger model
npj Quantum Information (2019)