Abstract
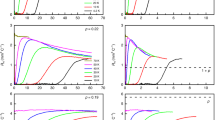
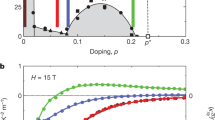
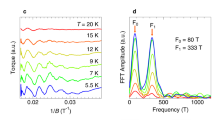
The perfectly linear temperature dependence of the electrical resistivity observed as T → 0 in a variety of metals close to a quantum critical point1,2,3,4 is a major puzzle of condensed-matter physics5. Here we show that T-linear resistivity as T → 0 is a generic property of cuprates, associated with a universal scattering rate. We measured the low-temperature resistivity of the bilayer cuprate Bi2Sr2CaCu2O8+δ and found that it exhibits a T-linear dependence with the same slope as in the single-layer cuprates Bi2Sr2CuO6+δ (ref. 6), La1.6−xNd0.4SrxCuO4 (ref. 7) and La2−xSrxCuO4 (ref. 8), despite their very different Fermi surfaces and structural, superconducting and magnetic properties. We then show that the T-linear coefficient (per CuO2 plane), A1□, is given by the universal relation A1□TF = h/2e2, where e is the electron charge, h is the Planck constant and TF is the Fermi temperature. This relation, obtained by assuming that the scattering rate 1/τ of charge carriers reaches the Planckian limit9,10, whereby ħ/τ = kBT, works not only for hole-doped cuprates6,7,8,11,12 but also for electron-doped cuprates13,14, despite the different nature of their quantum critical point and strength of their electron correlations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors (L.T. or C.P.) upon reasonable request.
References
Löhneysen, H. v. et al. Non-Fermi-liquid behavior in a heavy-fermion alloy at a magnetic instability. Phys. Rev. Lett. 72, 3262–3265 (1994).
Fournier, P. et al. Insulator–metal crossover near optimal doping in Pr2−xCexCuO4: Anomalous normal-state low temperature resistivity. Phys. Rev. Lett. 81, 4720–4723 (1998).
Grigera, S. A. et al. Magnetic field-tuned quantum criticality in the metallic ruthenate Sr3Ru2CuO7. Science 294, 329–332 (2001).
Doiron-Leyraud, N. et al. Correlation between linear resistivity and T c in the Bechgaard salts and the pnictide superconductor Ba(Fe1 − xCox)2As2. Phys. Rev. B 80, 214531 (2009).
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226–229 (2005).
Martin, S. et al. Normal-state transport properties of Bi2+xSr2−yCuO6+δ single crystals. Phys. Rev. B 41, 846–849 (1990).
Daou, R. et al. Linear temperature dependence of resistivity and change in the Fermi surface at the pseudogap critical point of a high-T c superconductor. Nat. Phys. 5, 31–34 (2009).
Cooper, R. A. et al. Anomalous criticality in the electrical resistivity of La2−xSrxCuO4. Science 323, 603–607 (2009).
Zaanen, J. Why the temperature is high. Nature 430, 512–513 (2004).
Bruin, J. A. N. et al. Similarity of scattering rates in metals showing T-linear resistivity. Science 339, 804–807 (2013).
Collignon, C. et al. Fermi-surface transformation across the pseudogap critical point of the cuprate superconductor La1.6−xNd0.4SrxCuO4. Phys. Rev. B 95, 224517 (2017).
Doiron-Leyraud, N. et al. Pseudogap phase of cuprate superconductors confined by Fermi surface topology. Nat. Commun. 8, 2044 (2017).
Jin, K. et al. Link between spin fluctuations and electron pairing in copper oxide superconductors. Nature 476, 73–75 (2011).
Sarkar, T. et al. Fermi surface reconstruction and anomalous low-temperature resistivity in electron-doped La2 − xCexCuO4. Phys. Rev. B 96, 155449 (2017).
Löhneysen, H. v. et al. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).
Dagan, Y. et al. Evidence for a quantum phase transition in Pr2 − xCexCuO4 from transport measurements. Phys. Rev. Lett. 92, 167001 (2004).
Tafti, F. F. et al. Nernst effect in the electron-doped cuprate superconductor Pr2 − xCexCuO4: superconducting fluctuations, upper critical field H c2, and the origin of the T c dome. Phys. Rev. B 90, 024519 (2014).
Motoyama, E. M. et al. Spin correlations in the electron-doped high-transition-temperature superconductor Nd2-xCexCuO4. Nature 445, 186–189 (2007).
Matt, C. E. et al. Electron scattering, charge order, and pseudogap physics in La1.6−xNd0.4SrxCuO4: an angle-resolved photoemission spectroscopy study. Phys. Rev. B 92, 134524 (2015).
Yoshida, T. et al. Systematic doping evolution of the underlying Fermi surface of La2−xSr xCuO4. Phys. Rev. B 74, 224510 (2006).
Kaminski, A. et al. Change of Fermi-surface topology in Bi2Sr2CaCu2O8+δ with doping. Phys. Rev. B 73, 174511 (2006).
Benhabib, S. et al. Collapse of the normal-state pseudogap at a Lifshitz transition in the Bi2Sr2CaCu2O8+δ cuprate superconductor. Phys. Rev. Lett. 114, 147001 (2015).
Hussey, N. E. et al. Phenomenology of the normal-state in-plane transport properties of high-T c cuprates. J. Phys. Condens. Matter 20, 123201 (2008).
Fauqué, B. et al. Dispersion of the odd magnetic resonant mode in near-optimally doped Bi2Sr2CaCu2O8+δ. Phys. Rev. B 76, 214512 (2007).
Tranquada, J. M. et al. Coexistence of, and competition between, superconductivity and charge-stripe order in La1.62−xNd0.4SrxCuO4. Phys. Rev. Lett. 78, 338 (1997).
Hussey, N. E. et al. Generic strange metal behavior of overdoped cuprates. J. Phys. Conf. Series 449, 012004 (2013).
Hayes, I. M. et al. Scaling between magnetic field and temperature in the high-temperature superconductor BaFe2(As1−xPx)2. Nat. Phys. 12, 919 (2016).
Matsui, H. et al. Evolution of the pseudogap across the magnet–superconductor phase boundary of Nd2−xCexCuO4. Phys. Rev. B 75, 224514 (2007).
Helm, T. et al. Evolution of the Fermi surface of the electron-doped high-temperature superconductor Nd2−xCexCuO4 revealed by Shubnikov–de Haas oscillations. Phys. Rev. Lett. 103, 157002 (2009).
Helm, T. et al. Correlation between Fermi surface transformations and superconductivity in the electron-doped high-T c superconductor Nd2−xCexCuO4. Phys. Rev. B 92, 094501 (2015).
Yu, W. et al. Magnetic-field dependence of the low-temperature specific heat of the electron-doped superconductor Pr1.85Ce0.15CuO4. Phys. Rev. B 72, 212512 (2005).
Bangura, A. et al. Fermi surface and electronic homogeneity of the overdoped cuprate superconductor Tl2Ba2CuO6+δ as revealed by quantum oscillations. Phys. Rev. B. 82, 140501R (2010).
Loram, J. W. et al. Evidence on the pseudogap and the condensate from the electronic specific heat. J. Phys. Chem. Solids 62, 59–64 (2001).
Nakamae, S. et al. Electronic ground state of heavily overdoped nonsuperconducting La2−xSrxCuO4. Phys. Rev. B 68, 100502R (2003).
Wang, Y. et al. Weak-coupling d-wave BCS superconductivity and unpaired electrons in overdoped La2−xSrxCuO4 single crystals. Phys. Rev. B 76, 064512 (2007).
Michon, B. et al. Thermodynamic evidence of quantum criticality in cuprate superconductors. Preprint at https://arxiv.org/abs/1804.08502 (2018).
Davison, R. A., Schalm, K. & Zaanen, J. Holographic duality and the resistivity of strange metals. Phys. Rev. B 89, 245116 (2014).
Hartnoll, S. A. Theory of universal incoherent metallic transport. Nat. Phys. 11, 54–61 (2015).
Song, X. Y. et al. Strongly correlated metal built from Sachdev-Ye-Kitaev models. Phys. Rev. Lett. 119, 216601 (2017).
Konstantinovic, Z., Li, Z. Z. & Raffy, H. Temperature dependence of the Hall effect in single-layer and bilayer Bi2Sr2Can–1CunOy thin films at various oxygen contents. Phys. Rev. B 62, R11989(R) (2000).
Charpentier, S. et al. Antiferromagnetic fluctuations and the Hall effect of electron-doped cuprates: possibility of a quantum phase transition at underdoping. Phys. Rev. B 81, 104519 (2010).
Hussey, N. E. et al. Dichotomy in the T-linear resistivity in hole-doped cuprates. Phil. Trans. R. Soc. A 369, 1626–1639 (2011).
Falicov, L. M. & Stachowiak, H. Theory of the de Haas–van Alphen effect in a system of coupled orbits. Application to magnesium. Phys. Rev. 147, 505 (1966).
Acknowledgements
The authors would like to thank K. Behnia, C. Bourbonnais, R. Greene, S. Hartnoll, N. Hussey, M.-H. Julien, D. Maslov, J. Paglione, S. Sachdev, A.-M. Tremblay and J. Zaanen for fruitful discussions. A portion of this work was performed at the LNCMI, a member of the European Magnetic Field Laboratory (EMFL). C.P. acknowledges funding from the French ANR SUPERFIELD, and the LABEX NEXT. P.F. and L.T. acknowledge support from the Canadian Institute for Advanced Research (CIFAR) and funding from the Natural Sciences and Engineering Research Council of Canada (NSERC), the Fonds de recherche du Québec - Nature et Technologies (FRQNT) and the Canada Foundation for Innovation (CFI). L.T. acknowledges support from a Canada Research Chair. This research was undertaken thanks in part to funding from the Canada First Research Excellence Fund. Part of this work was funded by the Gordon and Betty Moore Foundation’s EPiQS Initiative (grant GBMF5306 to L.T.).
Author information
Authors and Affiliations
Contributions
A.L., S.B., W.T., B.V., D.V. and C.P. performed the transport measurements at the LNCMI. A.L., F.L., M.L. and N.D.-L. performed the transport measurements at Sherbrooke. H.R., P.A.-S. and Z.Z.L. prepared the Bi2212 film, which was then characterized by A.L., H.R., P.A.-S., Z.Z.L. and D.C. M.D. and P.F. prepared and characterized the PCCO films. A.L., F.L., L.T. and C.P. wrote the manuscript, in consultation with all authors. L.T. and C.P. co-supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
10 Figures, 4 Tables, 11 References
Rights and permissions
About this article
Cite this article
Legros, A., Benhabib, S., Tabis, W. et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nature Phys 15, 142–147 (2019). https://doi.org/10.1038/s41567-018-0334-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0334-2
This article is cited by
-
Flat bands, strange metals and the Kondo effect
Nature Reviews Materials (2024)
-
Low-Field Hall effect, Pseudogap and Magnetic Textures in the Bi\(_{2}\)Sr\(_{2}\)CaCu\(_{2}\)O\(_{8+x}\) Superconductor
Journal of Superconductivity and Novel Magnetism (2024)
-
Superconductivity from a melted insulator in Josephson junction arrays
Nature Physics (2023)
-
Transport properties and doping evolution of the Fermi surface in cuprates
Scientific Reports (2023)
-
Signature of quantum criticality in cuprates by charge density fluctuations
Nature Communications (2023)