Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Superradiant emission from colour centres in diamond

Nature Physics volume 14, pages 1168–1172 (2018)Cite this article

Subjects

Abstract

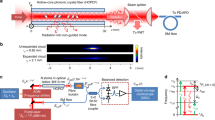
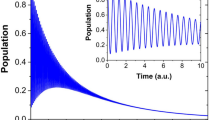
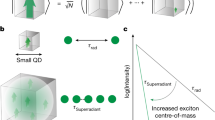
Superradiance is a fundamental collective effect where radiation is amplified by the coherence of multiple emitters1. Superradiance plays a prominent role in optics (where it enables the design of lasers with substantially reduced linewidths2,3) and quantum mechanics4, and is even used to explain cosmological observations such as Hawking radiation from black holes5. Resonators coupled to spin ensembles6,7,8 are promising future building blocks of integrated quantum devices that will involve superradiance. As such, it is important to study its fundamental properties within such devices. Although experiments in the strong-coupling regime have shown oscillatory behaviour in these systems9,10, a clear signature of Dicke superradiance has so far been missing. Here we explore superradiance in a system composed of a three-dimensional lumped element resonator in the fast cavity limit inductively coupled to an inhomogeneously broadened ensemble of nitrogen–vacancy centres. We observe a superradiant pulse being emitted a trillion times faster than the decay for an individual nitrogen–vacancy centre. This is further confirmed by the nonlinear scaling of the emitted radiation intensity with respect to the ensemble size. Our work provides the foundation for future quantum technologies including solid-state superradiant masers2.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental setup.
Fig. 2: Cavity response under varying drive powers.
Fig. 3: Dynamics of the superradiant decay.
Fig. 4: Nonlinear scaling of the emitted radiation intensity.

Similar content being viewed by others

References

  1. Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).

    Article  ADS  Google Scholar 

  2. Bohnet, J. G. et al. A steady-state superradiant laser with less than one intracavity photon. Nature 484, 78–81 (2012).

    Article  ADS  Google Scholar 

  3. Meiser, D., Ye, J., Carlson, D. R. & Holland, M. J. Prospects for a millihertz-linewidth laser. Phys. Rev. Lett. 102, 163601 (2009).

    Article  ADS  Google Scholar 

  4. Bonifacio, R., Schwendimann, P. & Haake, F. Quantum statistical theory of superradiance. II. Phys. Rev. A 4, 854–864 (1971).

    Article  ADS  Google Scholar 

  5. Thorne, K. S. Black Holes and Time Warps: Einstein’s Outrageous Legacy 430–435 (Norton, New York, NY, 1994).

  6. Schuster, D. I. et al. High-cooperativity coupling of electron-spin ensembles to superconducting cavities. Phys. Rev. Lett. 105, 140501 (2010).

    Article  ADS  Google Scholar 

  7. Kubo, Y. et al. Hybrid quantum circuit with a superconducting qubit coupled to a spin ensemble. Phys. Rev. Lett. 107, 220501 (2011).

    Article  ADS  Google Scholar 

  8. Amsüss, R. et al. Cavity QED with magnetically coupled collective spin states. Phys. Rev. Lett. 107, 060502 (2011).

    Article  ADS  Google Scholar 

  9. Putz, S. et al. Protecting a spin ensemble against decoherence in the strong-coupling regime of cavity QED. Nat. Phys. 10, 720–724 (2014).

    Article  Google Scholar 

  10. Rose, B. et al. Coherent Rabi dynamics of a superradiant spin ensemble in a microwave cavity. Phys. Rev. X 7, 031002 (2017).

    Google Scholar 

  11. Gross, M. & Haroche, S. Superradiance: an essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982).

    Article  ADS  Google Scholar 

  12. Julsgaard, B. & Mølmer, K. Dynamical evolution of an inverted spin ensemble in a cavity: inhomogeneous broadening as a stabilizing mechanism. Phys. Rev. A 86, 063810 (2012).

    Article  ADS  Google Scholar 

  13. Mlynek, J. A., Abdumalikov, A. A., Eichler, C. & Wallraff, A. Observation of Dicke superradiance for two artificial atoms in a cavity with high decay rate. Nat. Commun. 5, 5186 (2014).

    Article  ADS  Google Scholar 

  14. Eschner, J., Raab, C., Schmidt-Kaler, F. & Blatt, R. Light interference from single atoms and their mirror images. Nature 413, 495–498 (2001).

    Article  ADS  Google Scholar 

  15. DeVoe, R. G. & Brewer, R. G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 76, 2049–2052 (1996).

    Article  ADS  Google Scholar 

  16. Scheibner, M. et al. Superradiance of quantum dots. Nat. Phys. 3, 106–110 (2007).

    Article  Google Scholar 

  17. Gross, M., Fabre, C., Pillet, P. & Haroche, S. Observation of near-infrared Dicke superradiance on cascading transitions in atomic sodium. Phys. Rev. Lett. 36, 1035–1038 (1976).

    Article  ADS  Google Scholar 

  18. Skribanowitz, N., Herman, I. P., MacGillivray, J. C. & Feld, M. S. Observation of Dicke superradiance in optically pumped HF gas. Phys. Rev. Lett. 30, 309–312 (1973).

    Article  ADS  Google Scholar 

  19. Inouye, S. et al. Superradiant Rayleigh scattering from a Bose–Einstein condensate. Science 285, 571–574 (1999).

    Article  Google Scholar 

  20. Ten Brinke, N. & Schützhold, R. Dicke superradiance as a nondestructive probe for quantum quenches in optical lattices. Phys. Rev. A 92, 013617 (2015).

    Article  ADS  Google Scholar 

  21. Norcia, M. A., Winchester, M. N., Cline, J. R. K. & Thompson, J. K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2, e1601231 (2016).

    Article  ADS  Google Scholar 

  22. Gross, M., Goy, P., Fabre, C., Haroche, S. & Raimond, J. M. Maser oscillation and microwave superradiance in small systems of Rydberg atoms. Phys. Rev. Lett. 43, 343–346 (1979).

    Article  ADS  Google Scholar 

  23. Kaluzny, Y., Goy, P., Gross, M., Raimond, J. M. & Haroche, S. Observation of self-induced Rabi oscillations in two-level atoms excited inside a resonant cavity: the ringing regime of superradiance. Phys. Rev. Lett. 51, 1175–1178 (1983).

    Article  ADS  Google Scholar 

  24. Temnov, V. V. & Woggon, U. Superradiance and subradiance in an inhomogeneously broadened ensemble of two-level systems coupled to a low-Q cavity. Phys. Rev. Lett. 95, 243602 (2005).

    Article  ADS  Google Scholar 

  25. Delanty, M., Rebić, S. & Twamley, J. Superradiance and phase multistability in circuit quantum electrodynamics. New J. Phys. 13, 053032 (2011).

    Article  ADS  Google Scholar 

  26. Jodoin, R. & Mandel, L. Superradiance in an inhomogeneously broadened atomic system. Phys. Rev. A 9, 873–884 (1974).

    Article  ADS  Google Scholar 

  27. Bennett, S. D. et al. Phonon-induced spin–spin interactions in diamond nanostructures: application to spin squeezing. Phys. Rev. Lett. 110, 156402 (2013).

    Article  ADS  Google Scholar 

  28. Lambert, N. et al. Superradiance with an ensemble of superconducting flux qubits. Phys. Rev. B 94, 224510 (2016).

    Article  ADS  Google Scholar 

  29. Shammah, N., Lambert, N., Nori, F. & De Liberato, S. Superradiance with local phase-breaking effects. Phys. Rev. A 96, 023863 (2017).

    Article  ADS  Google Scholar 

  30. Angerer, A. et al. Collective strong coupling with homogeneous Rabi frequencies using a 3D lumped element microwave resonator. Appl. Phys. Lett. 109, 033508 (2016).

    Article  ADS  Google Scholar 

  31. Doherty, M. W. et al. The nitrogen–vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).

    Article  ADS  Google Scholar 

  32. Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).

    Article  Google Scholar 

  33. Bienfait, A. et al. Controlling spin relaxation with a cavity. Nature 531, 74–77 (2016).

    Article  ADS  Google Scholar 

  34. Astner, T. et al. Solid-state electron spin lifetime limited by phononic vacuum modes. Nat. Mater. 17, 313–317 (2018).

    Article  ADS  Google Scholar 

  35. Nefedkin, N. E., Andrianov, E. S., Pukhov, A. A. & Vinogradov, A. P. Superradiance enhancement by bad-cavity resonator. Laser Phys. 27, 065201 (2017).

    Article  ADS  Google Scholar 

  36. Tavis, M. & Cummings, F. W. Exact solution for an N-molecule-radiation-field Hamiltonian. Phys. Rev. 170, 379–384 (1968).

    Article  ADS  Google Scholar 

  37. Purcell, E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).

    Article  Google Scholar 

  38. Grezes, C. et al. Storage and retrieval of microwave fields at the single-photon level in a spin ensemble. Phys. Rev. A 92, 020301 (2015).

    Article  ADS  Google Scholar 

  39. Jin, L. et al. Proposal for a room-temperature diamond maser. Nat. Commun. 6, 8251 (2015).

    Article  Google Scholar 

  40. Weiner, J. M., Cox, K. C., Bohnet, J. G., Chen, Z. & Thompson, J. K. Superradiant Raman laser magnetometer. Appl. Phys. Lett. 101, 261107 (2012).

    Article  ADS  Google Scholar 

  41. Acosta, V. M. et al. Diamonds with a high density of nitrogen–vacancy centers for magnetometry applications. Phys. Rev. B 80, 115202 (2009).

    Article  ADS  Google Scholar 

  42. Bienfait, A. et al. Reaching the quantum limit of sensitivity in electron spin resonance. Nat. Nanotech. 11, 253 (2016).

    Article  ADS  Google Scholar 

  43. Nefedkin, N. E. et al. Superradiance of non-Dicke states. Opt. Express 25, 2790–2804 (2017).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We would like to thank D. Krimer, M. Zens, S. Rotter and H. Ritsch for discussions and G. Wachter for help with the setup of the laser system. The experimental effort has been supported by the Top-/Anschubfinanzierung grant of the TU Wien and the JTF project “The Nature of Quantum Networks” (ID 60478). A.A. and T.A. acknowledge support by the Austrian Science Fund (FWF) in the framework of the Doctoral School “Building Solids for Function” Project W1243. K.N. acknowledges support from the MEXT KAKENHI Grant-in-Aid for Scientific Research on Innovative Areas “Science of Hybrid Quantum Systems” no. 15H05870. J.I. acknowledges support by the Japan Society for the Promotion of Science KAKENHI grant no. 26220903 and grant no. 17H02751. J.S. acknowledges financial support from the Wiener Wissenschafts- und TechnologieFonds (WWTF) project No MA16-066 (“SEQUEX”).

Author information

Author notes

  1. Kirill Streltsov

    Present address: Institute for Theoretical Physics, Universität Ulm, Ulm, Germany

  2. Stefan Putz

    Present address: Department of Physics, Princeton University, Princeton, NJ, USA

Authors and Affiliations

  1. Vienna Center for Quantum Science and Technology, Atominstitut, TU Wien, Vienna, Austria

    Andreas Angerer, Kirill Streltsov, Thomas Astner, Stefan Putz, Jörg Schmiedmayer & Johannes Majer

  2. Sumitomo Electric Industries Ltd., Itami, Japan

    Hitoshi Sumiya

  3. National Institutes for Quantum and Radiological Science and Technology, Takasaki, Japan

    Shinobu Onoda

  4. Research Centre for Knowledge Communities, University of Tsukuba, Tsukuba, Japan

    Junichi Isoya

  5. NTT Basic Research Laboratories, NTT Corporation, Atsugi, Japan

    William J. Munro

  6. National Institute of Informatics, Hitotsubashi, Tokyo, Japan

    William J. Munro & Kae Nemoto

  7. Wolfgang Pauli Institute c/o Faculty of Mathematics, Universität Wien, Vienna, Austria

    Johannes Majer

Authors
  1. Andreas Angerer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kirill Streltsov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas Astner
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Stefan Putz
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hitoshi Sumiya
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Shinobu Onoda
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Junichi Isoya
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. William J. Munro
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Kae Nemoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Jörg Schmiedmayer
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Johannes Majer
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.A., S.P., T.A., J.S. and J.M designed and set up the experiment. A.A. and K.S. carried out the measurements under the supervision of J.M. W.J.M. and K.N provided the theoretical framework. J.I., S.O. and H.S. characterized and provided the diamond sample. A.A. wrote the manuscript, to which all authors suggested improvements.

Corresponding authors

Correspondence to Andreas Angerer or Johannes Majer.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Angerer, A., Streltsov, K., Astner, T. et al. Superradiant emission from colour centres in diamond. Nature Phys 14, 1168–1172 (2018). https://doi.org/10.1038/s41567-018-0269-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0269-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing