Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Imaging quantum fluctuations near criticality

Nature Physics volume 14, pages 1205–1210 (2018)Cite this article

Subjects

Abstract

A quantum phase transition (QPT) occurs between two competing phases of matter at zero temperature, driven by quantum fluctuations. Although the presence of these fluctuations is well established, they have not been locally imaged in space, and their local dynamics has not been studied so far. We use a scanning superconducting quantum interference device to image quantum fluctuations near the QPT from a superconductor to an insulator. We find fluctuations of the diamagnetic response in both space and time that survive well below the transition temperature, demonstrating their quantum nature. The fluctuations appear as telegraph-like noise with a range of characteristic times and a non-monotonic temperature dependence, revealing unexpected quantum granularity. The lateral dimension of these fluctuations grows towards criticality, offering a new measurable length scale. Our results provide physical insight into the reorganization of phases across a QPT, with implications for any theoretical description. This paves a new route for future quantum information applications.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Scanning SQUID measurements near the quantum phase transition show fluctuations in space and time.
Fig. 2: Spatial and temporal distribution of events.
Fig. 3: The temperature range and length scale of fluctuations grow towards the critical point.
Fig. 4: The spatial configuration of fluctuations changes in each cooldown.
Fig. 5: Simulations of susceptibility fluctuations.

Similar content being viewed by others

References

  1. Rubiño-Martín, J. A., Rebolo, R. & Mediavilla, E. The Cosmic Microwave Background: From Quantum Fluctuations to the Present Universe: XIX Canary Islands Winter School on Astrophysics (Cambridge Univ. Press, Cambridge, 2010).

  2. Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, Cambridge, 2011).

  3. Löhneysen, Hv, Rosch, A., Vojta, M. & Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).

    Article  ADS  Google Scholar 

  4. Endres, M. et al. The ‘Higgs’ amplitude mode at the two-dimensional superfluid/Mott insulator transition. Nature 487, 454–458 (2012).

    Article  ADS  Google Scholar 

  5. Rançon, A. & Dupuis, N. Quantum XY criticality in a two-dimensional Bose gas near the Mott transition. Europhys. Lett. 104, 16002 (2013).

    Article  ADS  Google Scholar 

  6. Paalanen, M. A., Hebard, A. F. & Ruel, R. R. Low-temperature insulating phases of uniformly disordered two-dimensional superconductors. Phys. Rev. Lett. 69, 1604–1607 (1992).

    Article  ADS  Google Scholar 

  7. Yazdani, A. & Kapitulnik, A. Superconducting–insulating transition in two-dimensional a-MoGe thin films. Phys. Rev. Lett. 74, 3037–3040 (1995).

    Article  ADS  Google Scholar 

  8. Markovic, N., Christiansen, C. & Goldman, A. M. Thickness–magnetic field phase diagram at the superconductor–insulator transition in 2D. Phys. Rev. Lett. 81, 5217–5220 (1998).

    Article  ADS  Google Scholar 

  9. Baturina, T. I., Strunk, C., Baklanov, M. R. & Satta, A. Quantum metallicity on the high-field side of the superconductor–insulator transition. Phys. Rev. Lett. 98, 127003 (2007).

    Article  ADS  Google Scholar 

  10. Crane, R. W. et al. Fluctuations, dissipation, and nonuniversal superfluid jumps in two-dimensional superconductors. Phys. Rev. Lett. B 75, 094506 (2007).

    Article  ADS  Google Scholar 

  11. Strack, P. & Jakubezyk, P. Fluctuations of imbalanced fermionic superfluids in two dimensions induce continuous quantum phase transitions and non-Fermi-liquid behavior. Phys. Rev X 4, 021012 (2014).

    Google Scholar 

  12. Shi, X., Lin, P. V., Sasagawa, T., Dobrosavljević, V., & Popović, D. Two-stage magnetic-field-tuned superconductor–insulator transition in underdoped La2–xSrxCuO4.Nat. Phys. 10, 437–443 (2014).

    Article  Google Scholar 

  13. Sherman, D. et al. The Higgs mode in disordered superconductors close to a quantum phase transition. Nat. Phys. 11, 188–192 (2015).

    Article  Google Scholar 

  14. Poran, S. et al. Quantum criticality at the superconductor–insulator transition revealed by specific heat measurements. Nat. Comm. 8, 14464 (2017).

    Article  ADS  Google Scholar 

  15. Ghosal, A., Randeria, M. & Trivedi, N. Role of spatial amplitude fluctuations in highly disordered s-wave superconductors. Phys. Rev. Lett. 81, 3940–3943 (1998).

    Article  ADS  Google Scholar 

  16. Ghosal, A., Randeria, M. & Trivedi, N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 65, 014501 (2001).

    Article  ADS  Google Scholar 

  17. Bouadim, K., Loh, Y. L. M., Randeria, M. & Trivedi, N. Single and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 7, 884–889 (2011).

    Article  Google Scholar 

  18. Kowal, D. & Ovadyahu, Z. Scale dependent superconductor-insulator transition. Physica C 468, 322–325 (2008).

    Article  ADS  Google Scholar 

  19. Sacepe, B. et al. Disorder-Induced inhomogeneities of the superconducting state close to the superconductor–insulator transition. Phys. Rev. Lett. 101, 157006 (2008).

    Article  ADS  Google Scholar 

  20. Sacepe, B. et al. Localization of preformed Cooper pairs in disordered superconductors. Nat. Phys. 7, 239–244 (2011).

    Article  Google Scholar 

  21. Mondal, M. et al. Phase fluctuations in a strongly disordered s-wave NbN superconductor close to the metal–insulator transition. Phys. Rev. Lett. 106, 047001 (2011).

    Article  ADS  Google Scholar 

  22. Ganguly, R. et al. Magnetic field induced emergent inhomogeneity in a superconducting film with weak and homogeneous disorder. Phys. Rev. B 96, 054509 (2017).

    Article  ADS  Google Scholar 

  23. Carbillet, C. et al. Confinement of superconducting fluctuations due to emergent electronic inhomogeneities. Phys. Rev. B 93, 144509 (2016).

    Article  ADS  Google Scholar 

  24. Kirtley, J. R. Fundamental studies of superconductors using scanning magnetic imaging. Rep. Prog. Phys. 73, 126501 (2010).

    Article  ADS  Google Scholar 

  25. Wissberg, S., Frydman, A. & Kalisky, B. Local view of superconducting fluctuations. Appl. Phys. Lett. 112, 262602 (2018).

    Article  ADS  Google Scholar 

  26. Goldman, A. M. & Markovic, N. Superconductor-insulator transitions in the two-dimensional limit. Phys. Today 51, 39–41 (November,1998).

    Article  Google Scholar 

  27. Lim, B. S., Rahtu, A. & Gordon, R. G. Atomic layer deposition of transition metals. Nat. Mater. 2, 749–754 (2003).

    Article  ADS  Google Scholar 

  28. Shiino, T. et al. Improvement of the critical temperature of superconducting NbTiN and NbN thin films using the AlN buffer layer. Supercond. Sci. Technol. 23, 045004 (2010).

    Article  ADS  Google Scholar 

  29. Burdastyh, M. V. et al. Superconductor–insulator transition in NbTiN films. JETP Lett. 106, 749–753 (2017).

    Article  ADS  Google Scholar 

  30. Gardner, B. W. et al. Scanning superconducting quantum interference device susceptometry. Rev. Sci. Instrum. 72, 2361–2364 (2001).

    Article  ADS  Google Scholar 

  31. Huber, M. E. et al. Gradiometric micro-SQUID susceptometer for scanning measurements of mesoscopic samples. Rev. Sci. Instrum. 79, 053704 (2008).

    Article  ADS  Google Scholar 

  32. Trivedi, N., Scalettar, R. T. & Randeria., M. Superconductor–insulator transition in a disordered electronic system. Phys. Rev. B 54, R3756(R) (1996).

    Article  ADS  Google Scholar 

  33. Wallin, M., Sorensen, E. S., Girvin, S. M. & Young, A. P. Superconductor–insulator transition in two-dimensional dirty boson systems. Phys. Rev. B 49, 12115–12139 (1994).

    Article  ADS  Google Scholar 

  34. Swanson, M., Loh, Y. L., Randeria, M. & Trivedi, T. Dynamical conductivity across the disorder-tuned superconductor–insulator transition. Phys. Rev. X 4, 021007 (2014).

    Google Scholar 

Download references

Acknowledgements

We are grateful for technical help from I. Volotchenko and E. A. Persky, and for discussions with D. Roditchev. A.K. and B.K. were supported by the European Research Council grant ERC-2014-STG-639792 and the Israel Science Foundation grant ISF-1281/17. A.F. and N.T. acknowledge support from the Israel US bi-national foundation grant no. 2014325. A.K., A.F and B.K acknowledge the COST Action CA16218. B.K. acknowledges the QuantERA ERA-NET Cofund in Quantum Technologies (project no. 731473). T.I.B. acknowledges support by the Russian Science Foundation (project no. 14-22-00143) and by the Consejería de Educación, Cultura y Deporte (Comunidad de Madrid) through the talent attraction programme, ref. 2016-T3/IND-1839.

Author information

Authors and Affiliations

  1. Department of Physics and Institute of Nanotechnology and Advanced Materials, Bar Ilan University, Ramat Gan, Israel

    A. Kremen, T. I. Baturina, A. Frydman & B. Kalisky

  2. Department of Physics, The Ohio State University, Columbus, OH, USA

    H. Khan & N. Trivedi

  3. Department of Physics and Astrophysics, University of North Dakota, Grand Forks, ND, USA

    Y. L. Loh

  4. Institute of Semiconductor Physics, Novosibirsk, Russia

    T. I. Baturina

  5. Novosibirsk State University, Novosibirsk, Russia

    T. I. Baturina

Authors
  1. A. Kremen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. L. Loh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. I. Baturina
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. N. Trivedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. A. Frydman
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. B. Kalisky
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.K. and B.K. designed the experiment and performed the measurements. A.F. initiated the research and participated in experiments. T.I.B. provided the samples and related measurements. H.K., Y.L.L. and N.T. performed the calculations. N.T, A.F. and B.K. prepared the manuscript with input from all co-authors.

Corresponding authors

Correspondence to A. Frydman or B. Kalisky.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figures 1–6

Supplementary Video

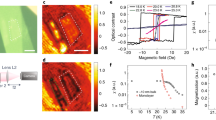
Evolution of susceptibility in sample S1 with temperature. Top panel: susceptibility maps at different temperatures in S1. The images, STD and susceptibility signal describe the local evolution of susceptibility as the sample heats slightly above Tc and cooled down again. At T > Tc no diamagnetic response is observed and the image reflects the SQUID noise. At T < Tc the image shows the presence of darker puddles and streaks of weaker superconductivity, which survive well below Tc. Bottom panel, left: standard deviation (STD) versus temperature, extracted from susceptibility maps shown in the top panel. The STD is normalized to the highest value in each curve. Bottom panel, right: susceptibility signal versus temperature. The vertical bars show the range of susceptibility values in each image.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kremen, A., Khan, H., Loh, Y.L. et al. Imaging quantum fluctuations near criticality. Nature Phys 14, 1205–1210 (2018). https://doi.org/10.1038/s41567-018-0264-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0264-z

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing