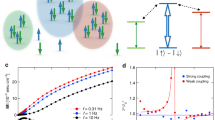
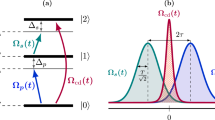
Abstract
In three-level quantum systems, interference between two simultaneously driven excitation pathways can give rise to effects such as coherent population trapping1,2 and electromagnetically induced transparency3. The possibility to exploit these effects has made three-level systems a cornerstone of quantum optics. Coherent driving of the third available transition forms a closed-contour interaction (CCI), which yields fundamentally new phenomena, including phase-controlled coherent population trapping4,5 and phase-controlled coherent population dynamics6. Despite attractive prospects, prevalent dephasing in experimental systems suitable for CCI driving has made its observation elusive7,8,9,10. Here, we exploit recently developed methods for coherent manipulation of nitrogen–vacancy electronic spins to implement and study highly coherent CCI driving of a single spin. Our experiments reveal phase-controlled quantum interference, reminiscent of electron dynamics on a closed loop threaded by a magnetic flux, which we synthesize from the driving-field phase11. Owing to the nature of the dressed states created under CCI, we achieve nearly two orders of magnitude improvement of the dephasing times, even for moderate drive strengths. CCI driving constitutes a novel approach to coherent control of few-level systems, with potential for applications in quantum sensing or quantum information processing.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Gray, H. R., Whitley, R. M. & Stroud, C. R. Coherent trapping of atomic populations. Opt. Lett. 3, 218–220 (1978).
Agap’ev, B. D., Gorny, M. B., Matisov, B. G. & Rozhdestvenski, Y. V. Coherent population trapping in quantum systems. Phys.-Uspekhi 36, 763–793 (1993).
Fleischhauer, M., Imamoglu, A. & Marangos, J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005).
Kosachiov, D. V., Matisov, B. G. & Rozhdestvensky, Y. V. Coherent phenomena in multilevel systems with closed interaction contour. J. Phys. B 25, 2473–2488 (1992).
Windholz, L. Coherent population trapping in multi-level atomic systems. Phys. Scr. 2001, 81–91 (2001).
Buckle, S., Barnett, S., Knight, P., Lauder, M. & Pegg, D. Atomic interferometers. Opt. Acta 33, 1129–1140 (1986).
Yamamoto, K., Ichimura, K. & Gemma, N. Enhanced and reduced absorptions via quantum interference: Solid system driven by a rf field. Phys. Rev. A 58, 2460–2466 (1998).
Korsunsky, E. A., Leinfellner, N., Huss, A., Baluschev, S. & Windholz, L. Phase-dependent electromagnetically induced transparency. Phys. Rev. A 59, 2302–2305 (1999).
Li, H. et al. Electromagnetically induced transparency controlled by a microwave field. Phys. Rev. A 80, 023820 (2009).
Preethi, T. M. et al. Phase-sensitive microwave optical double resonance in an N system. EPL Europhys. Lett. 95, 34005 (2011).
Roushan, P. et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 13, 146–151 (2017).
Phillips, D. F., Fleischhauer, A., Mair, A., Walsworth, R. L. & Lukin, M. D. Storage of light in atomic vapor. Phys. Rev. Lett. 86, 783–786 (2001).
Vanier, J. Atomic clocks based on coherent population trapping: a review. Appl. Phys. B 81, 421–442 (2005).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Northup, T. E. & Blatt, R. Quantum information transfer using photons. Nat. Photon. 8, 356–363 (2014).
Shore, B. W. Manipulating Quantum Structures Using Laser Pulses (Cambridge Univ. Press, Cambridge, 2011)
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Doherty, M. W. et al. The nitrogen–vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Barfuss, A., Teissier, J., Neu, E., Nunnenkamp, A. & Maletinsky, P. Strong mechanical driving of a single electron spin. Nat. Phys. 11, 820–824 (2015).
Dobrovitski, V., Fuchs, G., Falk, A., Santori, C. & Awschalom, D. Quantum control over single spins in diamond. Annu. Rev. Condens. Matter Phys. 4, 23–50 (2013).
MacQuarrie, E. R. et al. Coherent control of a nitrogen–vacancy center spin ensemble with a diamond mechanical resonator. Optica 2, 233–238 (2015).
Cai, J.-M. et al. Robust dynamical decoupling with concatenated continuous driving. New J. Phys. 14, 113023 (2012).
Xu, X. et al. Coherence-protected quantum gate by continuous dynamical decoupling in diamond. Phys. Rev. Lett. 109, 070502 (2012).
MacQuarrie, E. R., Gosavi, T. A., Bhave, S. A. & Fuchs, G. D. Continuous dynamical decoupling of a single diamond nitrogen–vacancy center spin with a mechanical resonator. Phys. Rev. B 92, 224419 (2015).
Acosta, V. M. et al. Temperature dependence of the nitrogen–vacancy magnetic resonance in diamond. Phys. Rev. Lett. 104, 070801 (2010).
Joas, T., Waeber, A. M., Braunbeck, G. & Reinhard, F. Quantum sensing of weak radio-frequency signals by pulsed Mollow absorption spectroscopy. Nat. Commun. 8, 964 (2017).
Stark, A. et al. Narrow-bandwidth sensing of high-frequency fields with continuous dynamical decoupling. Nat. Commun. 8, 1105 (2017).
Abobeih, M. H., One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Fang, K. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 13, 465–471 (2017).
Acknowledgements
We thank A. Retzker, N. Aharon, A. Nunnenkamp and H. Ribeiro for fruitful discussions and valuable input. We gratefully acknowledge financial support through the NCCR QSIT, a competence centre funded by the Swiss NSF, through the Swiss Nanoscience Institute, by the EU FP7 project DIADEMS (grant no. 611143) and through SNF Project Grant 169321.
Author information
Authors and Affiliations
Contributions
A.B., J.T. and P.M conceived the experiment. A.B. and J.K. performed the experiment and analysed the data, together with M.K. and P.M.. L.T. and J.T. provided support in measurement software. A.B. and M.K. performed the theoretical modelling of our data. A.B., M.K. and P.M. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes, figures and references
Rights and permissions
About this article
Cite this article
Barfuss, A., Kölbl, J., Thiel, L. et al. Phase-controlled coherent dynamics of a single spin under closed-contour interaction. Nature Phys 14, 1087–1091 (2018). https://doi.org/10.1038/s41567-018-0231-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0231-8
This article is cited by
-
Nonreciprocal transition between two indirectly coupled energy levels
Frontiers of Physics (2022)
-
Highly efficient charging and discharging of three-level quantum batteries through shortcuts to adiabaticity
Frontiers of Physics (2022)
-
Experimental realization of phase-controlled dynamics with hybrid digital–analog approach
npj Quantum Information (2021)
-
Optically driving the radiative Auger transition
Nature Communications (2021)
-
Spin–phonon interactions in silicon carbide addressed by Gaussian acoustics
Nature Physics (2019)