Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Reconstructing the topology of optical polarization knots

Nature Physics volume 14, pages 1079–1082 (2018)Cite this article

Subjects

Abstract

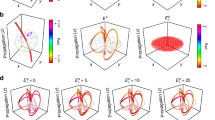
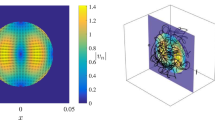
Knots are topological structures describing how a looped thread can be arranged in space. Although most familiar as knotted material filaments, it is also possible to create knots in singular structures within three-dimensional physical fields such as fluid vortices1 and the nulls of optical fields2,3,4. Here we produce, in the transverse polarization profile of optical beams, knotted lines of circular transverse polarization. We generate and observe both simple torus knots and links as well as the topologically more complicated figure-eight knot. The presence of these knotted polarization singularities endows a nontrivial topological structure on the entire three-dimensional propagating wavefield. In particular, the contours of constant polarization azimuth form Seifert surfaces of high genus5, which we are able to resolve experimentally in a process we call seifertometry. This analysis reveals a level of topological complexity, present in all experimentally generated polarization fields, that goes beyond the conventional reconstruction of polarization singularity lines.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic of the experimental apparatus used to generate and characterize polarization singularity knots.
Fig. 2: Topological traits of torus structures.
Fig. 3: Topological characterization and seifertometry of an optical figure-eight knot.

Similar content being viewed by others

References

  1. Kleckner, D. & Irvine, W. T. M. Creation and dynamics of knotted vortices. Nat. Phys. 9, 253–258 (2013).

    Article  Google Scholar 

  2. Berry, M. V. & Dennis, M. R. Knotted and linked phase singularities in monochromatic waves. Proc. R. Soc. A 457, 2251–2263 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  3. Leach, J., Dennis, M. R., Courtial, J. & Padgett, M. J. Laser beams: knotted threads of darkness. Nature 432, 165 (2004).

    Article  ADS  Google Scholar 

  4. Dennis, M. R., King, R. P., Jack, B., O’Holleran, K. & Padgett, M. J. Isolated optical vortex knots. Nat. Phys. 6, 118–121 (2010).

    Article  Google Scholar 

  5. Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots (American Mathematical Society, Providence, RI, 2004).

  6. Abrikosov, A. A. On the magnetic properties of superconductors of the second group. Sov. Phys. JETP 5, 1174–1182 (1957).

    Google Scholar 

  7. Donnelly, R. J. Experimental Superfluidity (University of Chicago Press, Chicago, 1967).

  8. Nye, J. F. & Berry, M. V. Dislocations in wave trains. Proc. Roy. Soc. A. 336, 165–190 (1974).

    Article  ADS  MathSciNet  Google Scholar 

  9. Nye, J. F. Natural Focusing and Fine Structure of Light (IoP Publishing, Bristol, 1999).

  10. Dennis, M. R., O’Holleran, K. & Padgett, M. J. in Progress in Optics Vol. 53 (ed. Wolf, E.) 293–363 (Elsevier, Amsterdam, 2009).

  11. Martinez, A. et al. Mutually tangled colloidal knots and induced defect loops in nematic fields. Nat. Mater. 13, 258–263 (2014).

    Article  ADS  Google Scholar 

  12. Dennis, M. R. & Bode, B. Constructing a polynomial whose nodal set is the three-twist knot 52. J. Phys. A 50, 265204 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  13. Bode, B., Dennis, M. R., Foster, D. & King, R. P. Knotted fields and explicit fibrations for lemniscate knots. Proc. R. Soc. A 473, 20160829 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  14. Nye, J. F. Phase saddles in light beams. J. Opt. 13, 075709 (2011).

    Article  ADS  Google Scholar 

  15. Flossmann, F., O’Holleran, K., Dennis, M. R. & Padgett, M. J. Polarization singularities in 2D and 3D speckle fields. Phys. Rev. Lett. 100, 203902 (2008).

    Article  ADS  Google Scholar 

  16. Galvez, E. J., Khadka, S., Schubert, W. H. & Nomoto, S. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre–Gauss and polarization modes of light. Appl. Opt. 51, 2925–2934 (2012).

    Article  ADS  Google Scholar 

  17. Cardano, F., Karimi, E., Marrucci, L., de Lisio, C. & Santamato, E. Generation and dynamics of optical beams with polarization singularities. Opt. Express 21, 8815–8820 (2013).

    Article  ADS  Google Scholar 

  18. Freund, I. Optical Möbius strips in three−dimensional ellipse fields: I. Lines of circular polarization. Opt. Commun. 283, 1–15 (2010).

    Article  ADS  Google Scholar 

  19. Bauer, T. et al. Observation of optical polarization Möbius strips. Science 347, 964–966 (2015).

    Article  ADS  Google Scholar 

  20. Bauer, T., Neugebauer, M., Leuchs, G. & Banzer, P. Optical polarization Möbius strips and points of purely transverse spin density. Phys. Rev. Lett. 117, 013601 (2016).

    Article  ADS  Google Scholar 

  21. Galvez, E. J. et al. Multitwist Möbius strips and twisted ribbons in the polarization of paraxial light beams. Sci. Rep. 7, 13653 (2017).

    Article  ADS  Google Scholar 

  22. Garcia-Etxarri, A. Optical polarization Möbius strips on all−dielectric optical scatterers. ACS Photonics 4, 1159–1164 (2017).

    Article  Google Scholar 

  23. Bolduc, E., Bent, N., Santamato, E., Karimi, E., & Boyd, R. W. Exact solution to simultaneous intensity and phase encryption with a single phase-only hologram. Opt. Lett. 38, 3546–3549 (2013).

    Article  ADS  Google Scholar 

  24. Taylor, A. J. & other SPOCK contributors. pyknotid knot identification toolkit v0.5.3. https://github.com/SPOCKnots/pyknotid (Accessed 9 May 2018).

  25. Larocque, H. et al. Arbitrary optical wavefront shaping via spin-to-orbit coupling. J. Opt. 18, 124002 (2016).

    Article  ADS  Google Scholar 

  26. Romero, J. et al. Entangled optical vortex links. Phys. Rev. Lett. 106, 100407 (2011).

    Article  ADS  Google Scholar 

  27. Fickler, R., Lapkiewicz, R., Ramelow, S. & Zeilinger, A. Quantum entanglement of complex photon polarization patterns in vector beams. Phys. Rev. A 89, 060301 (2013).

    Article  Google Scholar 

  28. Karimi, E. et al. Spin–orbit hybrid entanglement of photons and quantum contextuality. Phys. Rev. A 82, 022115 (2010).

    Article  ADS  Google Scholar 

  29. Taylor, A. J. & Dennis, M. R. Vortex knots in tangled quantum eigenfunctions. Nat. Commun. 7, 12346 (2016).

    Article  ADS  Google Scholar 

  30. Bouchard, F. et al. Polarization shaping for control of nonlinear propagation. Phys. Rev. Lett. 117, 233903 (2016).

    Article  ADS  Google Scholar 

  31. Fickler, R. et al. Quantum entanglement of high angular momenta. Science 338, 640–643 (2012).

    Article  ADS  Google Scholar 

  32. Padgett, M. J., O’Holleran, K., King, R. P. & Dennis, M. R. Knotted and tangled threads of darkness in light beams. Contemp. Phys. 52, 265–279 (2011).

    Article  ADS  Google Scholar 

  33. Lorensen, W. E. & Cline, H. E. Marching cubes: a high resolution 3d surface construction algorithm. ACM Comput. Graph. 21, 163–169 (1987).

    Article  Google Scholar 

  34. Orlandini, E. & Whittington, S. G. Statistical topology of closed curves: some applications in polymer physics. Rev. Mod. Phys. 79, 611–642 (2007).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank F. Bouchard for his advice on using the SLM and P. Banzer for fruitful discussions. This work was supported by Canada Research Chair (CRC) and Canada Foundation for Innovation (CFI). R.F. acknowledges the financial support of the Banting postdoctoral fellowship of the NSERC. E.K. and R.W.B. acknowledge the support of the Canada Excellence Research Chairs (CERC) Program. D.S, A.J.T and M.R.D were supported by the Leverhulme Trust Research Programme grant no. RP2013-K-009, SPOCK: Scientific Properties of Complex Knots.

Author information

Authors and Affiliations

  1. Department of Physics, University of Ottawa, Ottawa Ontario, Canada

    Hugo Larocque, Dominic Mortimer, Robert Fickler, Robert W. Boyd & Ebrahim Karimi

  2. H. H. Wills Physics Laboratory, University of Bristol, Bristol, UK

    Danica Sugic, Alexander J. Taylor & Mark R. Dennis

  3. Institute of Optics, University of Rochester, Rochester, New York, NY, USA

    Robert W. Boyd

  4. School of Physics and Astronomy, University of Birmingham, Birmingham, UK

    Mark R. Dennis

  5. Department of Physics, Institute for Advanced Studies in Basic Sciences, Zanjan, Iran

    Ebrahim Karimi

Authors
  1. Hugo Larocque
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Danica Sugic
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dominic Mortimer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Alexander J. Taylor
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Robert Fickler
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Robert W. Boyd
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Mark R. Dennis
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Ebrahim Karimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

H.L. and D.S. designed the holograms used to generate the knots. H.L., D.M. and R.F. performed the experiment. D.S., A.J.T. and M.R.D. performed the topological analysis. R.W.B, M.R.D. and E.K. supervised all aspects of the project. All authors discussed the results and contributed to the text of the manuscript.

Corresponding author

Correspondence to Ebrahim Karimi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary notes, figures and references

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Larocque, H., Sugic, D., Mortimer, D. et al. Reconstructing the topology of optical polarization knots. Nature Phys 14, 1079–1082 (2018). https://doi.org/10.1038/s41567-018-0229-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0229-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics