Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Higher-order topology in bismuth

Nature Physics volume 14, pages 918–924 (2018)Cite this article

Subjects

An Author Correction to this article was published on 15 April 2020

An Author Correction to this article was published on 19 September 2018

This article has been updated

Abstract

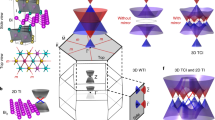
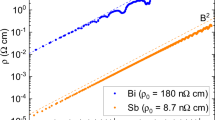
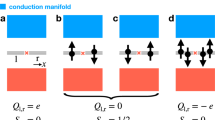
The mathematical field of topology has become a framework in which to describe the low-energy electronic structure of crystalline solids. Typical of a bulk insulating three-dimensional topological crystal are conducting two-dimensional surface states. This constitutes the topological bulk–boundary correspondence. Here, we establish that the electronic structure of bismuth, an element consistently described as bulk topologically trivial, is in fact topological and follows a generalized bulk–boundary correspondence of higher-order: not the surfaces of the crystal, but its hinges host topologically protected conducting modes. These hinge modes are protected against localization by time-reversal symmetry locally, and globally by the three-fold rotational symmetry and inversion symmetry of the bismuth crystal. We support our claim theoretically and experimentally. Our theoretical analysis is based on symmetry arguments, topological indices, first-principles calculations, and the recently introduced framework of topological quantum chemistry. We provide supporting evidence from two complementary experimental techniques. With scanning-tunnelling spectroscopy, we probe the signatures of the rotational symmetry of the one-dimensional states located at the step edges of the crystal surface. With Josephson interferometry, we demonstrate their universal topological contribution to the electronic transport. Our work establishes bismuth as a higher-order topological insulator.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Electronic structure of a HOTI with \(\hat C_3\) and \(\hat I\).
Fig. 2: Experimental observation of the alternating edge states on a bismuth (111) surface perpendicular to its trigonal axis.
Fig. 3: Evidence for hinge states from Josephson-interference experiments.

Change history

  • 15 April 2020

    An amendment to this paper has been published and can be accessed via a link at the top of the paper.

  • 19 September 2018

    In the version of this Article originally published, B. Andrei Bernevig was missing the following two additional affiliations: Physics Department, Freie Universitat Berlin, Berlin, Germany, and Max Planck Institute of Microstructure Physics, Halle, Germany. This has been corrected in the online versions of the Article.

References

  1. Liang, F., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).

    ADS  Google Scholar 

  2. Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).

    ADS  Google Scholar 

  3. Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).

    ADS  Google Scholar 

  4. Roy, R. Topological phases and the quantum spin hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).

    ADS  Google Scholar 

  5. Liang, F. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).

    ADS  Google Scholar 

  6. Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).

    Google Scholar 

  7. Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).

    ADS  Google Scholar 

  8. Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).

    ADS  Google Scholar 

  9. Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).

    ADS  Google Scholar 

  10. Dziawa, P. et al. Topological crystalline insulator states in PbSnSe. Nat. Mater. 11, 1023–1027 (2012).

    ADS  Google Scholar 

  11. Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).

    ADS  Google Scholar 

  12. Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 8, 800–803 (2012).

    Google Scholar 

  13. Xu, S.-Y. et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1-xSnxTe. Nat. Commun. 3, 1192 (2012).

    ADS  Google Scholar 

  14. Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  15. Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).

    ADS  Google Scholar 

  16. Song, Z., Fang, Z. & Fang, C. (d−2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).

    ADS  Google Scholar 

  17. Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).

    ADS  Google Scholar 

  18. Langbehn, J., Peng, Y., Trifunovic, L., von Oppen, F. & Brouwer, P. W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).

    ADS  Google Scholar 

  19. Klitzing, Kv, Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    ADS  Google Scholar 

  20. Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).

    ADS  Google Scholar 

  21. Avron, J. E. & Seiler, R. Quantization of the Hall conductance for general, multiparticle Schrödinger Hamiltonians. Phys. Rev. Lett. 54, 259–262 (1985).

    ADS  MathSciNet  Google Scholar 

  22. Niu, Q., Thouless, D. J. & Wu, Y.-S. Quantized hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).

    ADS  MathSciNet  Google Scholar 

  23. Kane, C. L. & Mele, E. J. z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).

    ADS  Google Scholar 

  24. Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).

    ADS  Google Scholar 

  25. Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006).

    ADS  Google Scholar 

  26. Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).

    ADS  Google Scholar 

  27. Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).

    ADS  Google Scholar 

  28. König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).

    ADS  Google Scholar 

  29. Roth, A. et al. Nonlocal transport in the quantum spin Hall state. Science 325, 294–297 (2009).

    ADS  Google Scholar 

  30. Wu, C., Bernevig, B. A. & Zhang, S.-C. Helical liquid and the edge of quantum spin Hall systems. Phys. Rev. Lett. 96, 106401 (2006).

    ADS  Google Scholar 

  31. Xu, Y., Xue, R. & Wan, S. Topological corner states on Kagome lattice-based chiral higher-order topological insulator. Preprint at https://arxiv.org/abs/1711.09202 (2017).

  32. Shapourian, H., Wang, Y. & Ryu, S. Topological crystalline superconductivity and second-order topological superconductivity in nodal-loop materials. Phys. Rev. B 97, 094508 (2018).

    ADS  Google Scholar 

  33. Lin, M. & Hughes, T. L. Topological quadrupolar semimetals. Preprint at https://arxiv.org/abs/1708.08457 (2017).

  34. Ezawa, M. Higher-order topological insulators and semimetals on the breathing Kagome and pyrochlore lattices. Phys. Rev. Lett. 120, 026801 (2018).

    ADS  Google Scholar 

  35. Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).

    ADS  Google Scholar 

  36. Geier, M., Trifunovic, L., Hoskam, M. & Brouwer, P. W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 97, 205135 (2018).

    ADS  Google Scholar 

  37. Fang, C. & Fu, L. Rotation anomaly and topological crystalline insulators. Preprint at https://arxiv.org/abs/1709.01929 (2017).

  38. Drozdov, I. K. et al. One-dimensional topological edge states of bismuth bilayers. Nat. Phys. 10, 664–669 (2014).

    Google Scholar 

  39. Li, C. et al. Magnetic field resistant quantum interferences in Josephson junctions based on bismuth nanowires. Phys. Rev. B 90, 245427 (2014).

    ADS  Google Scholar 

  40. Murani, A. et al. Ballistic edge states in bismuth nanowires revealed by SQUID interferometry. Nat. Commun. 8, 15941 (2017).

    ADS  Google Scholar 

  41. Wells, J. W. et al. Nondegenerate metallic states on Bi(114): a one-dimensional topological metal. Phys. Rev. Lett. 102, 096802 (2009).

    ADS  Google Scholar 

  42. Murakami, S. Quantum spin Hall effect and enhanced magnetic response by spin-orbit coupling. Phys. Rev. Lett. 97, 236805 (2006).

    ADS  Google Scholar 

  43. Takayama, A., Sato, T., Souma, S., Oguchi, T. & Takahashi, T. One-dimensional edge states with giant spin splitting in a bismuth thin film. Phys. Rev. Lett. 114, 066402 (2015).

    ADS  Google Scholar 

  44. Reis, F. et al. Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material. Science 357, 287–290 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  45. Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).

    ADS  Google Scholar 

  46. Vergniory, M. G. et al. Graph theory data for topological quantum chemistry. Phys. Rev. E 96, 023310 (2017).

    ADS  Google Scholar 

  47. Elcoro, L. et al. Double crystallographic groups and their representations on the Bilbao crystallographic server. J. Appl. Crystallogr. 50, 1457–1477 (2017).

    Google Scholar 

  48. Cano, J. et al. Building blocks of topological quantum chemistry: elementary band representations. Phys. Rev. B 97, 035139 (2018).

    ADS  Google Scholar 

  49. Bradlyn, B. et al. Band connectivity for topological quantum chemistry: band structures as a graph theory problem. Phys. Rev. B 97, 035138 (2018).

    ADS  Google Scholar 

  50. Cano, J. et al. Topology of disconnected elementary band representations. Phys. Rev. Lett. 120, 266401 (2018).

    ADS  Google Scholar 

  51. Ezawa, M. Minimal model for higher-order topological insulators and phosphorene. Preprint at https://arxiv.org/abs/1801.00437 (2018).

  52. Sessi, P. et al. Robust spin-polarized midgap states at step edges of topological crystalline insulators. Science 354, 1269–1273 (2016).

    ADS  MathSciNet  MATH  Google Scholar 

  53. Imhof, S. et al. Topolectrical circuit realization of topological corner modes. Preprint at https://arxiv.org/abs/1708.03647 (2017).

  54. Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).

    ADS  Google Scholar 

  55. Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).

    ADS  Google Scholar 

  56. Teo, J. C. Y., Fu, L. & Kane, C. L. Surface states and topological invariants in three-dimensional topological insulators: application to Bi1−xSbx. Phys. Rev. B 78, 045426 (2008).

    ADS  Google Scholar 

  57. Liu, Y. & Allen, R. E. Electronic structure of the semimetals Bi and Sb. Phys. Rev. B 52, 1566–1577 (1995).

    ADS  Google Scholar 

  58. Ohtsubo, Y. & Kimura, Shinichi Topological phase transition of single-crystal Bi based on empirical tight-binding calculations. New J. Phys. 18, 123015 (2016).

    ADS  Google Scholar 

  59. Fuseya, Y. et al. Origin of the large anisotropic g factor of holes in bismuth. Phys. Rev. Lett. 115, 216401 (2015).

    ADS  Google Scholar 

  60. Hart, S. et al. Induced superconductivity in the quantum spin Hall edge. Nat. Phys. 10, 638–643 (2014).

    Google Scholar 

  61. Della Rocca, M. L. et al. Measurement of the current-phase relation of superconducting atomic contacts. Phys. Rev. Lett. 99, 127005 (2007).

    ADS  Google Scholar 

  62. Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with majorana zero modes. Phys. Rev. B 95, 235305 (2017).

    ADS  Google Scholar 

  63. Aroyo, M. I. et al. Crystallography online: Bilbao crystallographic server. Bulg. Chem. Commun. 43, 183–197 (2011).

    Google Scholar 

  64. Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).

    ADS  Google Scholar 

  65. Kresse, G. & Furthmueller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).

    Google Scholar 

  66. Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).

    ADS  Google Scholar 

  67. Hobbs, D., Kresse, G. & Hafner, J. Fully unconstrained noncollinear magnetism within the projector augmented-wave method. Phys. Rev. B 62, 11556–11570 (2000).

    ADS  Google Scholar 

  68. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    ADS  Google Scholar 

  69. Perdew, J. P., Burke, K. & Ernzerhof, M. Perdew, Burke, and Ernzerhof reply. Phys. Rev. Lett. 80, 891–891 (1998).

    ADS  Google Scholar 

Download references

Acknowledgements

F.S. and T.N. acknowledge support from the Swiss National Science Foundation (grant number 200021_169061) and from the European Union’s Horizon 2020 research and innovation programme (ERC-StG-Neupert-757867-PARATOP). M.G.V. was supported by the IS2016-75862-P national project of the Spanish MINECO. A.M.C. wishes to thank the Kavli Institute for Theoretical Physics, which is supported by the National Science Foundation under grant number NSF PHY-1125915, for hosting during some stages of this work. A.M., S.S., A.Y.K., R.D., H.B. and S.G. thank M. Houzet, who drew their attention to recently published work on higher-order topological insulators. They were supported by the ANR grants DIRACFORMAG, MAGMA and JETS. A.Y. acknowledges support from NSF-MRSEC programmes through the Princeton Center for Complex Materials DMR-142054, NSF-DMR-1608848 and ARO-MURI programme W911NF-12-1-046. B.A.B. acknowledges support for the analytic work from the Department of Energy (de-sc0016239). B.A.B. also acknowledges support from a Simons Investigator Award, the Packard Foundation, and the Schmidt Fund for Innovative Research. The computational part of the Princeton work was performed under NSF EAGER grant DMR-1643312, ONR-N00014-14-1-0330, ARO MURI W911NF-12-1-0461 and NSF-MRSEC DMR-1420541.

Author information

Authors and Affiliations

  1. Department of Physics, University of Zurich, Zurich, Switzerland

    Frank Schindler, Ashley M. Cook & Titus Neupert

  2. Department of Physics, Princeton University, Princeton, NJ, USA

    Zhijun Wang

  3. Donostia International Physics Center, Donostia-San Sebastian, Spain

    Maia G. Vergniory

  4. Department of Applied Physics II, Faculty of Science and Technology, University of the Basque Country UPV/EHU, Bilbao, Spain

    Maia G. Vergniory

  5. IKERBASQUE, Basque Foundation for Science, Bilbao, Spain

    Maia G. Vergniory

  6. LPS, Univ. Paris-Sud, CNRS, UMR 8502, Paris, France

    Anil Murani, Alik Yu. Kasumov, Richard Deblock, Hélène Bouchiat & Sophie Guéron

  7. CSNSM, Univ. Paris-Sud, IN2P3, UMR 8609, Paris, France

    Shamashis Sengupta

  8. Institute of Microelectronics Technology and High Purity Materials RAS, Chernogolovka, Russia

    Alik Yu. Kasumov

  9. Joseph Henry Laboratories and Department of Physics, Princeton University, Princeton, NJ, USA

    Sangjun Jeon, Ali Yazdani & B. Andrei Bernevig

  10. Condensed Matter Physics and Materials Science Department, Brookhaven National Laboratory, Upton, NY, USA

    Ilya Drozdov

  11. Physics Department, Freie Universitat Berlin, Berlin, Germany

    B. Andrei Bernevig

  12. Max Planck Institute of Microstructure Physics, Halle, Germany

    B. Andrei Bernevig

Authors
  1. Frank Schindler
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhijun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Maia G. Vergniory
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ashley M. Cook
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Anil Murani
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Shamashis Sengupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Alik Yu. Kasumov
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Richard Deblock
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Sangjun Jeon
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Ilya Drozdov
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Hélène Bouchiat
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Sophie Guéron
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Ali Yazdani
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. B. Andrei Bernevig
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Titus Neupert
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

F.S., A.M.C., B.A.B. and T.N. carried out the theoretical analysis and model calculations. Z.W. and M.G.V. performed the first-principles calculations and topological quantum chemistry analysis. A.M., S.S., A.Y.K., R.D., H.B., and S.G. conceived and carried out the transport experiments including crystal growth. S.J., I.D. and A.Y. conceived and carried out the STM/STS experiments.

Corresponding author

Correspondence to Titus Neupert.

Ethics declarations

Competing Interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary text, Supplementary Figure S1-S3

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schindler, F., Wang, Z., Vergniory, M.G. et al. Higher-order topology in bismuth. Nature Phys 14, 918–924 (2018). https://doi.org/10.1038/s41567-018-0224-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0224-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing