Abstract
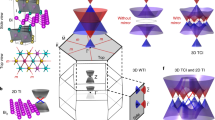
The mathematical field of topology has become a framework in which to describe the low-energy electronic structure of crystalline solids. Typical of a bulk insulating three-dimensional topological crystal are conducting two-dimensional surface states. This constitutes the topological bulk–boundary correspondence. Here, we establish that the electronic structure of bismuth, an element consistently described as bulk topologically trivial, is in fact topological and follows a generalized bulk–boundary correspondence of higher-order: not the surfaces of the crystal, but its hinges host topologically protected conducting modes. These hinge modes are protected against localization by time-reversal symmetry locally, and globally by the three-fold rotational symmetry and inversion symmetry of the bismuth crystal. We support our claim theoretically and experimentally. Our theoretical analysis is based on symmetry arguments, topological indices, first-principles calculations, and the recently introduced framework of topological quantum chemistry. We provide supporting evidence from two complementary experimental techniques. With scanning-tunnelling spectroscopy, we probe the signatures of the rotational symmetry of the one-dimensional states located at the step edges of the crystal surface. With Josephson interferometry, we demonstrate their universal topological contribution to the electronic transport. Our work establishes bismuth as a higher-order topological insulator.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
15 April 2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
19 September 2018
In the version of this Article originally published, B. Andrei Bernevig was missing the following two additional affiliations: Physics Department, Freie Universitat Berlin, Berlin, Germany, and Max Planck Institute of Microstructure Physics, Halle, Germany. This has been corrected in the online versions of the Article.
References
Liang, F., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).
Roy, R. Topological phases and the quantum spin hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).
Liang, F. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Dziawa, P. et al. Topological crystalline insulator states in PbSnSe. Nat. Mater. 11, 1023–1027 (2012).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 8, 800–803 (2012).
Xu, S.-Y. et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1-xSnxTe. Nat. Commun. 3, 1192 (2012).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Song, Z., Fang, Z. & Fang, C. (d−2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).
Langbehn, J., Peng, Y., Trifunovic, L., von Oppen, F. & Brouwer, P. W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).
Klitzing, Kv, Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Avron, J. E. & Seiler, R. Quantization of the Hall conductance for general, multiparticle Schrödinger Hamiltonians. Phys. Rev. Lett. 54, 259–262 (1985).
Niu, Q., Thouless, D. J. & Wu, Y.-S. Quantized hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).
Kane, C. L. & Mele, E. J. z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Roth, A. et al. Nonlocal transport in the quantum spin Hall state. Science 325, 294–297 (2009).
Wu, C., Bernevig, B. A. & Zhang, S.-C. Helical liquid and the edge of quantum spin Hall systems. Phys. Rev. Lett. 96, 106401 (2006).
Xu, Y., Xue, R. & Wan, S. Topological corner states on Kagome lattice-based chiral higher-order topological insulator. Preprint at https://arxiv.org/abs/1711.09202 (2017).
Shapourian, H., Wang, Y. & Ryu, S. Topological crystalline superconductivity and second-order topological superconductivity in nodal-loop materials. Phys. Rev. B 97, 094508 (2018).
Lin, M. & Hughes, T. L. Topological quadrupolar semimetals. Preprint at https://arxiv.org/abs/1708.08457 (2017).
Ezawa, M. Higher-order topological insulators and semimetals on the breathing Kagome and pyrochlore lattices. Phys. Rev. Lett. 120, 026801 (2018).
Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).
Geier, M., Trifunovic, L., Hoskam, M. & Brouwer, P. W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 97, 205135 (2018).
Fang, C. & Fu, L. Rotation anomaly and topological crystalline insulators. Preprint at https://arxiv.org/abs/1709.01929 (2017).
Drozdov, I. K. et al. One-dimensional topological edge states of bismuth bilayers. Nat. Phys. 10, 664–669 (2014).
Li, C. et al. Magnetic field resistant quantum interferences in Josephson junctions based on bismuth nanowires. Phys. Rev. B 90, 245427 (2014).
Murani, A. et al. Ballistic edge states in bismuth nanowires revealed by SQUID interferometry. Nat. Commun. 8, 15941 (2017).
Wells, J. W. et al. Nondegenerate metallic states on Bi(114): a one-dimensional topological metal. Phys. Rev. Lett. 102, 096802 (2009).
Murakami, S. Quantum spin Hall effect and enhanced magnetic response by spin-orbit coupling. Phys. Rev. Lett. 97, 236805 (2006).
Takayama, A., Sato, T., Souma, S., Oguchi, T. & Takahashi, T. One-dimensional edge states with giant spin splitting in a bismuth thin film. Phys. Rev. Lett. 114, 066402 (2015).
Reis, F. et al. Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material. Science 357, 287–290 (2017).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
Vergniory, M. G. et al. Graph theory data for topological quantum chemistry. Phys. Rev. E 96, 023310 (2017).
Elcoro, L. et al. Double crystallographic groups and their representations on the Bilbao crystallographic server. J. Appl. Crystallogr. 50, 1457–1477 (2017).
Cano, J. et al. Building blocks of topological quantum chemistry: elementary band representations. Phys. Rev. B 97, 035139 (2018).
Bradlyn, B. et al. Band connectivity for topological quantum chemistry: band structures as a graph theory problem. Phys. Rev. B 97, 035138 (2018).
Cano, J. et al. Topology of disconnected elementary band representations. Phys. Rev. Lett. 120, 266401 (2018).
Ezawa, M. Minimal model for higher-order topological insulators and phosphorene. Preprint at https://arxiv.org/abs/1801.00437 (2018).
Sessi, P. et al. Robust spin-polarized midgap states at step edges of topological crystalline insulators. Science 354, 1269–1273 (2016).
Imhof, S. et al. Topolectrical circuit realization of topological corner modes. Preprint at https://arxiv.org/abs/1708.03647 (2017).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).
Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).
Teo, J. C. Y., Fu, L. & Kane, C. L. Surface states and topological invariants in three-dimensional topological insulators: application to Bi1−xSbx. Phys. Rev. B 78, 045426 (2008).
Liu, Y. & Allen, R. E. Electronic structure of the semimetals Bi and Sb. Phys. Rev. B 52, 1566–1577 (1995).
Ohtsubo, Y. & Kimura, Shinichi Topological phase transition of single-crystal Bi based on empirical tight-binding calculations. New J. Phys. 18, 123015 (2016).
Fuseya, Y. et al. Origin of the large anisotropic g factor of holes in bismuth. Phys. Rev. Lett. 115, 216401 (2015).
Hart, S. et al. Induced superconductivity in the quantum spin Hall edge. Nat. Phys. 10, 638–643 (2014).
Della Rocca, M. L. et al. Measurement of the current-phase relation of superconducting atomic contacts. Phys. Rev. Lett. 99, 127005 (2007).
Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with majorana zero modes. Phys. Rev. B 95, 235305 (2017).
Aroyo, M. I. et al. Crystallography online: Bilbao crystallographic server. Bulg. Chem. Commun. 43, 183–197 (2011).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Furthmueller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Hobbs, D., Kresse, G. & Hafner, J. Fully unconstrained noncollinear magnetism within the projector augmented-wave method. Phys. Rev. B 62, 11556–11570 (2000).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Perdew, Burke, and Ernzerhof reply. Phys. Rev. Lett. 80, 891–891 (1998).
Acknowledgements
F.S. and T.N. acknowledge support from the Swiss National Science Foundation (grant number 200021_169061) and from the European Union’s Horizon 2020 research and innovation programme (ERC-StG-Neupert-757867-PARATOP). M.G.V. was supported by the IS2016-75862-P national project of the Spanish MINECO. A.M.C. wishes to thank the Kavli Institute for Theoretical Physics, which is supported by the National Science Foundation under grant number NSF PHY-1125915, for hosting during some stages of this work. A.M., S.S., A.Y.K., R.D., H.B. and S.G. thank M. Houzet, who drew their attention to recently published work on higher-order topological insulators. They were supported by the ANR grants DIRACFORMAG, MAGMA and JETS. A.Y. acknowledges support from NSF-MRSEC programmes through the Princeton Center for Complex Materials DMR-142054, NSF-DMR-1608848 and ARO-MURI programme W911NF-12-1-046. B.A.B. acknowledges support for the analytic work from the Department of Energy (de-sc0016239). B.A.B. also acknowledges support from a Simons Investigator Award, the Packard Foundation, and the Schmidt Fund for Innovative Research. The computational part of the Princeton work was performed under NSF EAGER grant DMR-1643312, ONR-N00014-14-1-0330, ARO MURI W911NF-12-1-0461 and NSF-MRSEC DMR-1420541.
Author information
Authors and Affiliations
Contributions
F.S., A.M.C., B.A.B. and T.N. carried out the theoretical analysis and model calculations. Z.W. and M.G.V. performed the first-principles calculations and topological quantum chemistry analysis. A.M., S.S., A.Y.K., R.D., H.B., and S.G. conceived and carried out the transport experiments including crystal growth. S.J., I.D. and A.Y. conceived and carried out the STM/STS experiments.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text, Supplementary Figure S1-S3
Rights and permissions
About this article
Cite this article
Schindler, F., Wang, Z., Vergniory, M.G. et al. Higher-order topology in bismuth. Nature Phys 14, 918–924 (2018). https://doi.org/10.1038/s41567-018-0224-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0224-7