Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Entropic effects in cell lineage tree packings

Nature Physics volume 14, pages 1016–1021 (2018)Cite this article

Subjects

A Publisher Correction to this article was published on 08 August 2018

This article has been updated

Abstract

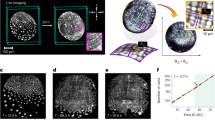
Optimal packings1,2 of unconnected objects have been studied for centuries3,4,5,6, but the packing principles of linked objects, such as topologically complex polymers7,8 or cell lineages9,10, are yet to be fully explored. Here, we identify and investigate a generic class of geometrically frustrated tree packing problems, arising during the initial stages of animal development when interconnected cells assemble within a convex enclosure10. Using a combination of 3D imaging, computational image analysis and mathematical modelling, we study the tree packing problem in Drosophila egg chambers, where 16 germline cells are linked by cytoplasmic bridges to form a branched tree. Our imaging data reveal non-uniformly distributed tree packings, in agreement with predictions from energy-based computations. This departure from uniformity is entropic and affects cell organization during the first stages of the animal’s development. Considering mathematical models of increasing complexity, we investigate spherically confined tree packing problems on convex polyhedra11 that generalize Platonic and Archimedean solids. Our experimental and theoretical results provide a basis for understanding the principles that govern positional ordering in linked multicellular structures, with implications for tissue organization and dynamics12,13.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Statistics of 3D CLT packings in D. melanogaster egg chambers.
Fig. 2: Entropic constraints drive departure from uniform distributions over possible cell-tree packings.
Fig. 3: Energy-based models confirm non-uniform CLT distributions and capture experimentally measured cell–cell adjacencies.

Similar content being viewed by others

Change history

  • 08 August 2018

    In the version of this Letter originally published, the citations to equation (1) in Fig. 3 caption and the main text were incorrect; they should have been to equation (2). This has now been corrected.

References

  1. Conway, J. H. & Sloane, N. J. A. Sphere Packings, Lattices, and Groups 3rd edn (Springer, New York, NY, 1999).

    Book  Google Scholar 

  2. Hales, T. C. et al. A revision of the proof of the Kepler conjecture. Discret. Comput. Geom. 44, 1–34 (2010).

    Article  MathSciNet  Google Scholar 

  3. Weaire, D. A short history of packing problems. Forma 14, 279–285 (1999).

    MathSciNet  MATH  Google Scholar 

  4. Donev, A. et al. Improving the density of jammed disordered packings using ellipsoids. Science 303, 990–993 (2004).

    Article  ADS  Google Scholar 

  5. Irvine, W. T. M., Vitelli, V. & Chaikin, P. M. Pleats in crystals on curved surfaces. Nature 468, 947–951 (2010).

    Article  ADS  Google Scholar 

  6. Meng, G., Paulose, J., Nelson, D. R. & Manoharan, V. N. Elastic instability of a crystal growing on a curved surface. Science 343, 634–637 (2014).

    Article  ADS  Google Scholar 

  7. Majikes, J. M., Nash, J. A. & LaBean, T. H. Competitive annealing of multiple DNA origami: formation of chimeric origami. New J. Phys. 18, 115001 (2016).

    Article  ADS  Google Scholar 

  8. Uhlmann, F. SMC complexes: from DNA to chromosomes. Nat. Rev. Mol. Cell Biol. 17, 399–412 (2016).

    Article  Google Scholar 

  9. Dayel, M. J. et al. Cell differentiation and morphogenesis in the colony-forming choanoflagellate Salpingoeca rosetta. Dev. Biol. 357, 73–82 (2011).

    Article  Google Scholar 

  10. Haglund, K., Nezis, I. P. & Stenmark, H. Structure and functions of stable intercellular bridges formed by incomplete cytokinesis during development. Commun. Integr. Biol. 4, 1–9 (2011).

    Article  Google Scholar 

  11. Johnson, N. W. Convex solids with regular faces. Can. J. Math. 18, 169–200 (1966).

    Article  Google Scholar 

  12. Hayashi, T. & Carthew, R. W. Surface mechanics mediate pattern formation in the developing retina. Science 431, 647–652 (2004).

    Google Scholar 

  13. Höhn, S., Honerkamp-Smith, A. R., Haas, P. A., Khuc Trong, P. & Goldstein, R. E. Dynamics of a volvox embryo turning itself inside out. Phys. Rev. Lett. 114, 178101 (2015).

    Article  ADS  Google Scholar 

  14. Lieberman-Aiden, E. et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326, 289–293 (2009).

    Article  ADS  Google Scholar 

  15. Tomer, R., Khairy, K., Amat, F. & Keller, P. J. Quantitative high-speed imaging of entire developing embryos with simultaneous multiview light-sheet microscopy. Nat. Methods 9, 755–763 (2012).

    Article  Google Scholar 

  16. Ohnesorge, F. & Binnig, G. True atomic resolution by atomic force microscopy through repulsive and attractive forces. Science 260, 1451–1456 (1993).

    Article  ADS  Google Scholar 

  17. Manoharan, V. N., Elsesser, M. T. & Pine, D. J. Dense packing and symmetry in small clusters of microspheres. Science 301, 483–487 (2003).

    Article  ADS  Google Scholar 

  18. Fletcher, A. J. L. Dry Stone Walls: History and Heritage (Amberley, Stroud, 2016).

    Google Scholar 

  19. Manoharan, V. N. Colloidal matter: packing, geometry, and entropy. Science 349, 1253751 (2015).

    Article  MathSciNet  Google Scholar 

  20. Lauga, E. & Brenner, M. P. Evaporation-driven assembly of colloidal particles. Phys. Rev. Lett. 93, 238301 (2004).

    Article  ADS  Google Scholar 

  21. Teich, E. G., van Anders, G., Klotsa, D., Dshemuchadse, J. & Glotzer, S. C. Clusters of polyhedra in spherical confinement. Proc. Natl Acad. Sci. USA 113, E669–E678 (2016).

    Article  Google Scholar 

  22. Doig, A. J. & Sternberg, M. J. Side-chain conformational entropy in protein folding. Protein Sci. 4, 2247–2251 (1995).

    Article  Google Scholar 

  23. Glass, D. S. & Riedel-Kruse, I. H. A genetically encoded adhesin toolbox for programming multicellular morphologies and patterns. Preprint at https://doi.org/10.1101/240721 (2017).

  24. Imran Alsous, J., Villoutreix, P., Berezhkovskii, A. M. & Shvartsman, S. Y. Collective growth in a small cell network. Curr. Biol. 27, 2670–2676 (2017).

    Article  Google Scholar 

  25. Gilbert, S. F. Developmental Biology 8th edn (Sinauer Associates, Sunderland, MA, 2006).

    Google Scholar 

  26. Turing, A. M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. B 237, 37–72 (1952).

    Article  ADS  MathSciNet  Google Scholar 

  27. Cartwright, J. & Arnold, J. M. Intercellular bridges in the embryo of the Atlantic squid, Loligo pealei. Development 57, 3–24 (1980).

    Google Scholar 

  28. Green, K. J., Viamontes, G. L. & Kirk, D. L. Mechanism of formation, ultrastructure, and function of the cytoplasmic bridge system during morphogenesis in Volvox. J. Cell. Biol. 91, 756–769 (1981).

    Article  Google Scholar 

  29. Becalska, A. N. & Gavis, E. R. Lighting up mRNA localization in Drosophila oogenesis. Development 136, 2493–2503 (2009).

    Article  Google Scholar 

  30. Green, K. J. & Kirk, D. L. Cleavage patterns, cell lineages, and development of a cytoplasmic bridge system in Volvox embryos. J. Cell. Biol. 91, 743–755 (1981).

    Article  Google Scholar 

  31. Cromwell, P. R. Polyhedra (Cambridge Univ. Press, Cambridge, 1997).

    MATH  Google Scholar 

  32. Thomson, J. J. On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Philos. Mag. 7, 237–265 (1904).

    Article  Google Scholar 

  33. Allen, M. P. & Tildesley, D. J. Computer Simulation of Liquids (Oxford Univ. Press, Oxford, 1989).

  34. Gould, H. & Tobochnik, J. Statistical and Thermal Physics: With Computer Applications (Princeton Univ. Press, Princeton, NJ, 2010).

  35. Rakhmanov, E. A., Saff, E. B. & Zhou, Y. M. in Computational Methods and Function Theory 1994 (Penang) Vol. 5 (eds Ali, R. M., Ruscheweyh, S. & Saff, E. B.) 293–309 (World Scientific, River Edge, NJ, 1995).

  36. Atiyah, M. & Sutcliffe, P. Polyhedra in physics, chemistry and geometry. Milan J. Math. 71, 33–58 (2003).

    Article  MathSciNet  Google Scholar 

  37. Erber, T. & Hockney, G. M. in Advances in Chemical Physics Vol. XCVIII (eds Prigogine, I. & Rice, S. A.) 495–594 (Wiley, New York, NY, 1997).

Download references

Acknowledgements

We thank G. Laevsky for expert help with imaging, and E. Gavis, A. Spradling, T. Orr-Weaver, F. Nijhout, L. Manning, H. Mattingly, Y. H. Song, T. Stern, S. Okuda and C. Doherty for helpful discussions. This work was supported by the National Science Foundation Science and Technology Center for Emergent Behaviors of Integrated Cellular Systems CBET-0939511 (J.I.A. and S.Y.S.), the NIH R01GM107103 (S.Y.S.), the WIN programme between Princeton University and the Weizmann Institute (P.V.), a James S. McDonnell Foundation Complex Systems Scholar Award (J.D.) and an Edmund F. Kelly Research Award from the MIT Department of Mathematics (J.D.). This research was partially supported by the Allen Discovery Center programme through The Paul G. Allen Frontiers Group.

Author information

Author notes

  1. These authors contributed equally: Jasmin Imran Alsous, Paul Villoutreix, Norbert Stoop.

Authors and Affiliations

  1. Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ, USA

    Jasmin Imran Alsous & Stanislav Y. Shvartsman

  2. The Lewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ, USA

    Jasmin Imran Alsous, Paul Villoutreix & Stanislav Y. Shvartsman

  3. Department of Molecular Genetics, Weizmann Institute of Science, Rehovot, Israel

    Paul Villoutreix

  4. Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Norbert Stoop & Jörn Dunkel

Authors
  1. Jasmin Imran Alsous
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paul Villoutreix
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Norbert Stoop
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Stanislav Y. Shvartsman
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jörn Dunkel
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors designed the research. J.I.A. performed the experiments. J.I.A., P.V. and N.S. analysed the data. N.S. and J.D. developed the theory. N.S. performed the simulations. All authors wrote the paper.

Corresponding author

Correspondence to Jörn Dunkel.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figures S1–S5, Supplementary References 1–14

Reporting Summary

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Imran Alsous, J., Villoutreix, P., Stoop, N. et al. Entropic effects in cell lineage tree packings. Nature Phys 14, 1016–1021 (2018). https://doi.org/10.1038/s41567-018-0202-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0202-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics