Abstract
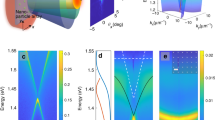
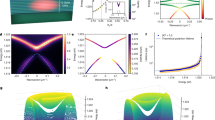
Bose–Einstein condensation is a remarkable manifestation of quantum statistics and macroscopic quantum coherence. Superconductivity and superfluidity have their origin in Bose–Einstein condensation. Ultracold quantum gases have provided condensates close to the original ideas of Bose and Einstein, while condensation of polaritons and magnons has introduced novel concepts of non-equilibrium condensation. Here, we demonstrate a Bose–Einstein condensate of surface plasmon polaritons in lattice modes of a metal nanoparticle array. Interaction of the nanoscale-confined surface plasmons with a room-temperature bath of dye molecules enables thermalization and condensation in picoseconds. The ultrafast thermalization and condensation dynamics are revealed by an experiment that exploits thermalization under propagation and the open-cavity character of the system. A crossover from a Bose–Einstein condensate to usual lasing is realized by tailoring the band structure. This new condensate of surface plasmon lattice excitations has promise for future technologies due to its ultrafast, room-temperature and on-chip nature.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Griffin, A., Snoke, D. & Stringari, S. Bose–Einstein Condensation (Cambridge Univ. Press, Cambridge, 1995).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Zwerger, W. The BCS–BEC Crossover and the Unitary Fermi Gas (Springer, Berlin, 2012).
Volovik, G. The Universe in a Helium Droplet (Oxford Univ. Press, Oxford, 2003).
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. Observation of Bose–Einstein condensation in a dilute atomic vapor. Science 269, 198–201 (1995).
Davis, K. B. et al. Bose–Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969–3973 (1995).
Bradley, C. C., Sackett, C. A., Tollett, J. J. & Hulet, R. G. Evidence of Bose–Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett. 75, 1687–1690 (1995).
Imamoglu, A., Ram, R. J., Pau, S. & Yamamoto, Y. Nonequilibrium condensates and lasers without inversion: Exciton-polariton lasers. Phys. Rev. A 53, 4250–4253 (1996).
Deng, H., Haug, H. & Yamamoto, Y. Exciton-polariton Bose–Einstein condensation. Rev. Mod. Phys. 82, 1489–1537 (2010).
Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013).
Sieberer, L. M., Huber, S. D., Altman, E. & Diehl, S. Dynamical critical phenomena in driven-dissipative systems. Phys. Rev. Lett. 110, 195301 (2013).
Byrnes, T., Kim, N. Y. & Yamamoto, Y. Exciton-polariton condensates. Nat. Phys. 10, 803–813 (2014).
Deng, H., Weihs, G., Santori, C., Bloch, J. & Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. Science 298, 199–202 (2002).
Kasprzak, J. et al. Bose–Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).
Balili, R., Hartwell, V., Snoke, D., Pfeiffer, L. & West, K. Bose–Einstein condensation of microcavity polaritons in a trap. Science 316, 1007–1010 (2007).
Baumberg, J. J. et al. Spontaneous polarization buildup in a room-temperature polariton laser. Phys. Rev. Lett. 101, 136409 (2008).
Amo, A. et al. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 457, 291–295 (2009).
Daskalakis, K. S., Maier, S. A., Murray, R. & Kéna-Cohen, S. Nonlinear interactions in an organic polariton condensate. Nat. Mater. 13, 271–278 (2014).
Plumhof, J. D., Stöferle, T., Mai, L., Scherf, U. & Mahrt, R. F. Room-temperature Bose–Einstein condensation of cavity exciton-polaritons in a polymer. Nat. Mater. 13, 247–252 (2014).
Lerario, G. et al. Room-temperature superfluidity in a polariton condensate. Nat. Phys. 13, 837–841 (2017).
Berloff, N. G. et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 16, 1120–1126 (2017).
Caputo, D. et al. Topological order and thermal equilibrium in polariton condensates. Nat. Mater. 17, 145–151 (2017).
Demokritov, S. O. et al. Bose–Einstein condensation of quasi-equilibrium magnons at room temperature under pumping. Nature 443, 430–433 (2006).
Giamarchi, T., Rüegg, C. & Tchernyshyov, O. Bose–Einstein condensation in magnetic insulators. Nat. Phys. 4, 198–204 (2008).
Klaers, J., Schmitt, J., Vewinger, F. & Weitz, M. Bose–Einstein condensation of photons in an optical microcavity. Nature 468, 545–548 (2010).
Marelic, J. et al. Spatiotemporal coherence of non-equilibrium multimode photon condensates. New J. Phys. 18, 103012 (2016).
Zou, S., Janel, N. & Schatz, G. C. Silver nanoparticle array structures that produce remarkably narrow plasmon lineshapes. J. Chem. Phys. 120, 10871–10875 (2004).
García de Abajo, F. J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 79, 1267–1290 (2007).
Auguié, B. & Barnes, W. L. Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 101, 143902 (2008).
Rodriguez, S. R. K., Feist, J., Verschuuren, M. A., Garcia Vidal, F. J. & Gómez Rivas, J. Thermalization and cooling of plasmon-exciton polaritons: towards quantum condensation. Phys. Rev. Lett. 111, 166802 (2013).
Martikainen, J.-P., Heikkinen, M. O. J. & Törmä, P. Condensation phenomena in plasmonics. Phys. Rev. A 90, 053604 (2014).
Schmitt, J. et al. Thermalization kinetics of light: From laser dynamics to equilibrium condensation of photons. Phys. Rev. A 92, 011602(R) (2015).
Khurgin, J. B. Ultimate limit of field confinement by surface plasmon polaritons. Faraday Discuss. 178, 109–122 (2015).
Maier, S. A. et al. Plasmonics—a route to nanoscale optical devices. Adv. Mater. 13, 1501–1505 (2001).
Novotny, L. & van Hulst, N. Antennas for light. Nat. Photon. 5, 83–90 (2011).
Zhou, W. et al. Lasing action in strongly coupled plasmonic nanocavity arrays. Nat. Nanotechnol. 8, 506–511 (2013).
Hakala, T. K. et al. Lasing in dark and bright modes of a finite-sized plasmonic lattice. Nat. Commun. 8, 13687 (2017).
Ramezani, M. et al. Plasmon-exciton-polariton lasing. Optica 4, 31–37 (2017).
Törmä, P. & Barnes, W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Progress Phys. 78, 013901 (2015).
Dridi, M. & Schatz, G. C. Model for describing plasmon-enhanced lasers that combines rate equations with finite-difference time-domain. J. Opt. Soc. Am. B 30, 2791–2797 (2013).
Kirton, P. & Keeling, J. Nonequilibrium model of photon condensation. Phys. Rev. Lett. 111, 100404 (2013).
Chiocchetta, A., Gambassi, A. & Carusotto, I. in Universal Themes of Bose–Einstein Condensation (eds Proukakis, N. P., Snoke D. W. & Littlewood, P. B.) (Cambridge Univ. Press, Cambridge, 2017).
Bajoni, D., Senellart, P., Lematre, A. & Bloch, J. Photon lasing in GaAs microcavity: Similarities with a polariton condensate. Phys. Rev. B 76, 201305 (2007).
Ketterle, W. & van Druten, N. J. Bose–Einstein condensation of a finite number of particles trapped in one or three dimensions. Phys. Rev. A 54, 656–660 (1996).
Kosterlitz, J. M. Kosterlitz–Thouless physics: a review of key issues. Rep. Progress Phys. 79, 026001 (2016).
Altman, E., Sieberer, L. M., Chen, L., Diehl, S. & Toner, J. Two-dimensional superfluidity of exciton polaritons requires strong anisotropy. Phys. Rev. X 5, 011017 (2015).
Chikkaraddy, R. et al. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 535, 127–130 (2016).
Guo, R., Hakala, T. K. & Törmä, P. Geometry dependence of surface lattice resonances in plasmonic nanoparticle arrays. Phys. Rev. B 95, 155423 (2017).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Kataja, M. et al. Surface lattice resonances and magneto-optical response in magnetic nanoparticle arrays. Nat. Commun. 6, 7072 (2015).
Julku, A. Condensation of Surface Lattice Resonance Excitations. MSc thesis, Aalto Univ. (2015).
Moilanen, A. J. Dispersion Relation and Density of States for Surface Lattice Resonance Excitations. MSc thesis, Aalto Univ. (2016).
Acknowledgements
We thank M. Heikkinen, D.-H. Kim, R. Moerland and M. Nečada for useful discussions. This work is dedicated in memory of D. Jin and her inspiring example. This work was supported by the Academy of Finland through its Centres of Excellence Programme (2012–2017) and under project numbers 284621, 303351 and 307419, and by the European Research Council (ERC-2013-AdG-340748-CODE). This article is based on work from COST Action MP1403 Nanoscale Quantum Optics, supported by COST (European Cooperation in Science and Technology). K.S.D. acknowledges financial support by a Marie Skłodowska-Curie Action (H2020-MSCA-IF-2016, project id 745115). Part of the research was performed at the Micronova Nanofabrication Centre, supported by Aalto University. The Triton cluster at Aalto University was used for the computations.
Author information
Authors and Affiliations
Contributions
P.T. initiated and supervised the project. T.K.H., A.J.M., R.G. and A.I.V. performed the experiments. A.J.M., T.K.H. and A.I.V. analysed the data. T.K.H., K.S.D. and H.T.R. built the experimental set-up. A.J.M., J.-P.M. and A.J. performed the theoretical modelling. R.G. fabricated the samples. All authors discussed the results. P.T., A.J.M. and T.K.H. wrote the manuscript together with all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figure 1–14, Supplementary References
Rights and permissions
About this article
Cite this article
Hakala, T.K., Moilanen, A.J., Väkeväinen, A.I. et al. Bose–Einstein condensation in a plasmonic lattice. Nature Phys 14, 739–744 (2018). https://doi.org/10.1038/s41567-018-0109-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0109-9
This article is cited by
-
Non-equilibrium Bose–Einstein condensation in photonic systems
Nature Reviews Physics (2022)
-
Magnetic on–off switching of a plasmonic laser
Nature Photonics (2022)
-
Modified Bose-Einstein condensation in an optical quantum gas
Nature Communications (2021)
-
Barrier-free reverse-intersystem crossing in organic molecules by strong light-matter coupling
Nature Communications (2021)
-
Sub-picosecond thermalization dynamics in condensation of strongly coupled lattice plasmons
Nature Communications (2020)