Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Classical topological order in the kinetics of artificial spin ice

Nature Physics volume 14, pages 723–727 (2018)Cite this article

Subjects

Abstract

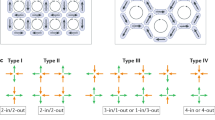
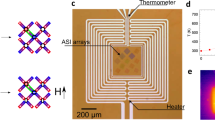
Systems of interacting nanomagnets known as artificial spin ice1,2,3,4 have allowed the design, realization and study of geometrically frustrated exotic collective states5,6,7,8,9,10 that are absent in natural magnets. We have experimentally measured11,12 the thermally induced moment fluctuations in the Shakti geometry of artificial spin ice. We show that its disordered moment configuration is a topological phase described by an emergent dimer-cover model13 with excitations that can be characterized as topologically charged defects. Examination of the low-energy dynamics of the system confirms that these effective topological charges have long lifetimes associated with their topological protection, that is, they can be created and annihilated only as charge pairs with opposite sign and are kinetically constrained. This manifestation of classical topological order14,15,16,17,18,19 demonstrates that geometrical design in nanomagnetic systems can lead to emergent, topologically protected kinetics that can limit pathways to equilibration and ergodicity.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: The Shakti lattice.
Fig. 2: Excitations above the ground state.
Fig. 3: The dimer model.
Fig. 4: Stability of topological charges.

Similar content being viewed by others

References

  1. Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).

    Article  ADS  Google Scholar 

  2. Heyderman, L. J. & Stamps, R. L. Artificial ferroic systems: novel functionality from structure, interactions and dynamics. J. Phys. Condens. Matter 25, 363201 (2013).

    Article  Google Scholar 

  3. Gilbert, I., Nisoli, C. & Schiffer, P. Frustration by design. Phys. Today 69, 54–59 (2016).

    Article  Google Scholar 

  4. Nisoli, C., Kapaklis, V. & Schiffer, P. Deliberate exotic magnetism via frustration and topology. Nat. Phys. 13, 200–203 (2017).

    Article  Google Scholar 

  5. Morrison, M. J., Nelson, T. R. & Nisoli, C. Unhappy vertices in artificial spin ice: new degeneracies from vertex frustration. New J. Phys. 15, 045009 (2013).

    Article  ADS  Google Scholar 

  6. Chern, G.-W., Morrison, M. J. & Nisoli, C. Degeneracy and criticality from emergent frustration in artificial spin ice. Phys. Rev. Lett. 111, 177201 (2013).

    Article  ADS  Google Scholar 

  7. Gilbert, I. et al. Emergent ice rule and magnetic charge screening from vertex frustration in artificial spin ice. Nat. Phys. 10, 670–675 (2014).

    Article  Google Scholar 

  8. Gilbert, I. et al. Emergent reduced dimensionality by vertex frustration in artificial spin ice. Nat. Phys. 12, 162–165 (2016).

    Article  Google Scholar 

  9. Perrin, Y., Canals, B. & Rougemaille, N. Extensive degeneracy, Coulomb phase and magnetic monopoles in artificial square ice. Nature 540, 410–413 (2016).

    Article  ADS  Google Scholar 

  10. Drisko, J., Marsh, T. & Cumings, J. Topological frustration of artificial spin ice. Nat. Commun. 8, 14009 (2017).

    Article  ADS  Google Scholar 

  11. Farhan, A. et al. Exploring hyper-cubic energy landscapes in thermally active finite artificial spin-ice systems. Nat. Phys. 9, 375–382 (2013).

    Article  Google Scholar 

  12. Farhan, A. et al. Direct observation of thermal relaxation in artificial spin ice. Phys. Rev. Lett. 111, 057204 (2013).

    Article  ADS  Google Scholar 

  13. Kasteleyn, P. W. The statistics of dimers on a lattice. Physica 27, 1209–1225 (1961).

    Article  ADS  Google Scholar 

  14. Castelnovo, C. & Chamon, C. Entanglement and topological entropy of the toric code at finite temperature. Phys. Rev. B 76, 184442 (2007).

    Article  ADS  Google Scholar 

  15. Henley, C. L. Classical height models with topological order. J. Phys. Condens. Matter 23, 164212 (2011).

    Article  ADS  Google Scholar 

  16. Castelnovo, C., Moessner, R. & Sondhi, S. L. Spin ice, fractionalization, and topological order. Annu. Rev. Condens. Matter Phys. 3, 35–55 (2012).

    Article  Google Scholar 

  17. Jaubert, L. D. C. et al. Topological-sector fluctuations and Curie-Law crossover in spin ice. Phys. Rev. X 3, 011014 (2013).

    Google Scholar 

  18. Lamberty, R. Z., Papanikolaou, S. & Henley, C. L. Classical topological order in Abelian and non-Abelian generalized height models. Phys. Rev. Lett. 111, 245701 (2013).

    Article  ADS  Google Scholar 

  19. Henley, C. L. The ‘Coulomb Phase’ in frustrated systems. Annu. Rev. Condens. Matter Phys. 1, 179–210 (2010).

    Article  ADS  Google Scholar 

  20. Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680–2684 (1935).

    Article  Google Scholar 

  21. Farhan, A. et al. Thermodynamics of emergent magnetic charge screening in artificial spin ice. Nat. Commun. 7, 12635 (2016).

    Article  ADS  Google Scholar 

  22. Kapaklis, V. et al. Thermal fluctuations in artificial spin ice. Nat. Nanotech. 9, 514–519 (2014).

    Article  ADS  Google Scholar 

  23. Anghinolfi, L. et al. Thermodynamic phase transitions in a frustrated magnetic metamaterial. Nat. Commun. 6, 8278 (2015).

    Article  ADS  Google Scholar 

  24. Morley, S. A. et al. Vogel-Fulcher-Tammann freezing of a thermally fluctuating artificial spin ice probed by X-ray photon correlation spectroscopy. Phys. Rev. B 95, 104422 (2017).

    Article  ADS  Google Scholar 

  25. Farhan, A., Derlet, P. M., Anghinolfi, L., Kleibert, A. & Heyderman, L. J. Magnetic charge and moment dynamics in artificial kagome spin ice. Phys. Rev. B 96, 064409 (2017).

    Article  ADS  Google Scholar 

  26. Stamps, R. L. Artificial spin ice: the unhappy wanderer. Nat. Phys. 10, 623–624 (2014).

    Article  Google Scholar 

  27. Ade, H. & Stoll, H. Near-edge X-ray absorption fine-structure microscopy of organic and magnetic materials. Nat. Mater. 8, 281–290 (2009).

    Article  ADS  Google Scholar 

  28. Cheng, X. M. & Keavney, D. J. Studies of nanomagnetism using synchrotron-based X-ray photoemission electron microscopy (X-PEEM). Rep. Prog. Phys. 75, 026501 (2012).

    Article  ADS  Google Scholar 

  29. Castelnovo, C., Moessner, R. & Sondhi, S. L. Thermal quenches in spin ice. Phys. Rev. Lett. 104, 107201 (2010).

    Article  ADS  Google Scholar 

  30. Banerjee, D. et al. Finite-volume energy spectrum, fractionalized strings, and low-energy effective field theory for the quantum dimer model on the square lattice. Phys. Rev. B 94, 115120 (2016).

    Article  ADS  Google Scholar 

  31. Ritort, F. & Sollich, P. Glassy dynamics of kinetically constrained models. Adv. Phys. 52, 219–342 (2003).

    Article  ADS  Google Scholar 

  32. Möller, G. & Moessner, R. Artificial square ice and related dipolar nanoarrays. Phys. Rev. Lett. 96, 237202 (2006).

    Article  ADS  Google Scholar 

  33. Budrikis, Z., Politi, P. & Stamps, R. L. Diversity enabling equilibration: disorder and the ground state in artificial spin ice. Phys. Rev. Lett. 107, 217204 (2011).

    Article  ADS  Google Scholar 

  34. Mostame, S., Castelnovo, C., Moessner, R. & Sondhi, S. L. Tunable nonequilibrium dynamics of field quenches in spin ice. Proc. Natl Acad. Sci. USA 111, 640–645 (2014).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The work of Y.L., J.S., D.G. and P.S. was funded by the US Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under grant no. DE-SC0010778. The work of C.N. and F.C. was carried out under the auspices of the NNSA of the US DOE at LANL under contract no. DE-AC52-06NA25396. C.N. wishes to thank the LDRD office for support and C. Castelnovo (University of Cambridge) for very useful discussions. The work of M.S. and K.D. was supported by the NSF through grant CBET 1336634. The work of A.M.A. and J.D.W. was supported by the NSF through grant DMR-1507048. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.

Author information

Authors and Affiliations

  1. Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Yuyang Lao, Mohammed Sheikh, Joseph Sklenar, Daniel Gardeazabal, Karin Dahmen & Peter Schiffer

  2. Frederick Seitz Materials Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Yuyang Lao, Joseph Sklenar, Daniel Gardeazabal & Peter Schiffer

  3. Theoretical Division, Institute for Materials Science, and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, NM, USA

    Francesco Caravelli & Cristiano Nisoli

  4. Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN, USA

    Justin D. Watts & Alan M. Albrecht

  5. School of Physics and Astronomy, University of Minnesota, Minneapolis, MN, USA

    Justin D. Watts

  6. Lawrence Berkeley National Laboratory (LBNL), Berkeley, CA, USA

    Andreas Scholl

  7. Department of Applied Physics and Department of Physics, Yale University, New Haven, CT, USA

    Peter Schiffer

Authors
  1. Yuyang Lao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francesco Caravelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammed Sheikh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Joseph Sklenar
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Daniel Gardeazabal
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Justin D. Watts
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Alan M. Albrecht
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Andreas Scholl
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Karin Dahmen
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Cristiano Nisoli
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Peter Schiffer
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Y.L. and J.S. prepared the lithographic patterns and performed the PEEM experiments with A.S. J.D.W. and A.M.A. prepared the permalloy deposition for the samples. Y.L. and D.G. digitalized the experimental images, analysed the data and rendered the data graphically. F.C. performed the numerical analysis and contributed to the theoretical interpretation. M.S. and K.D. assisted in data analysis. C.N. developed the topological framework for interpretation of the data. P.S. supervised the experimental work and coordinated the entire project.

Corresponding author

Correspondence to Peter Schiffer.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Extended data figures

Extended data figures 1–11

Supplementary video

The Supplementary Information file initially published online was corrupted and has now been replaced.

Methods

Supplementary methods, supplementary reference

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lao, Y., Caravelli, F., Sheikh, M. et al. Classical topological order in the kinetics of artificial spin ice. Nature Phys 14, 723–727 (2018). https://doi.org/10.1038/s41567-018-0077-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-018-0077-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing