Abstract
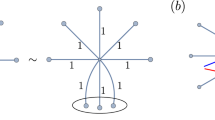
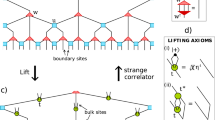
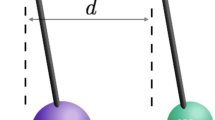
The gauge/gravity correspondence discovered two decades ago has had a profound influence on how the basic laws in physics should be formulated. In spite of the predictive power of holographic approaches (for example, when they are applied to strongly coupled condensed-matter physics problems), the fundamental reasons behind their success remain unclear. Recently, the role of quantum entanglement has come to the fore. Here we explore a quantity that connects gravity and quantum information in the light of the gauge/gravity correspondence. This is given by the minimal cross-section of the entanglement wedge that connects two disjoint subsystems in a gravity dual. In particular, we focus on various inequalities that are satisfied by this quantity. They suggest that it is a holographic counterpart of the quantity called entanglement of purification, which measures a bipartite correlation in a given mixed state. We give a heuristic argument that supports this identification based on a tensor network interpretation of holography. This predicts that the entanglement of purification satisfies the strong superadditivity for holographic conformal field theories.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Maldacena, J. M. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys.2, 231–252 (1998).
Ryu, S. & Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett.96, 181602 (2006).
Hubeny, V. E., Rangamani, M. & Takayanagi, T. A covariant holographic entanglement entropy proposal. J. High. Energy Phys.0707, 062 (2007).
Van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Rel. Gravit.42, 2323–2329 (2010).
Swingle, B. Entanglement renormalization and holography. Phys. Rev. D.86, 065007 (2012).
Miyaji, M. & Takayanagi, T. Surface/state correspondence as a generalized holography. Progr. Theor. Exp. Phys.2015, 073B03 (2015).
Pastawski, F., Yoshida, B., Harlow, D. & Preskill, J. Holographic quantum error-correcting codes: toy models for the bulk/boundary correspondence. J. High. Energy Phys.06, 149 (2015).
Hayden, P. et al. Holographic duality from random tensor networks. J. High. Energy Phys.11, 009 (2016).
Freedman, M. & Headrick, M. Bit threads and holographic entanglement. Commun. Math. Phys.352, 407–438 (2017).
Miyaji, M., Takayanagi, T. & Watanabe, K. From path integrals to tensor networks for AdS/CFT. Phys. Rev. D.95, 066004 (2017).
Caputa, P., Kundu, N., Miyaji, M., Takayanagi, T. & Watanabe, K. Anti-de Sitter space from optimization of path integrals in conformal field theories. Phys. Rev. Lett.119, 071602 (2017).
Caputa, P., Kundu, N., Miyaji, M., Takayanagi, T. & Watanabe, K. Liouville action as path-integral complexity: from continuous tensor networks to AdS/CFT. J. High. Energy Phys.11, 097 (2017).
Headrick, M. & Takayanagi, T. A holographic proof of the strong subadditivity of entanglement entropy. Phys. Rev. D76, 106013 (2007).
Hayden, P., Headrick, M. & Maloney, A. Holographic mutual information is monogamous. Phys. Rev. D87, 046003 (2013).
Headrick, M. General properties of holographic entanglement entropy. J. High. Energy Phys.03, 085 (2014).
Bao, N. et al. The holographic entropy cone. J. High. Energy Phys.09, 130 (2015).
Bengtsson, I. & Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement (Cambridge Univ. Press, Cambridge, 2006).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys.81, 865–942 (2009).
Czech, B., Karczmarek, J. L., Nogueira, F. & Van Raamsdonk, M. The gravity dual of a density matrix. Class. Quant. Grav.29, 155009 (2012).
Wall, A. C. Maximin surfaces, and the strong subadditivity of the covariant holographic entanglement entropy. Class. Quant. Grav.31, 225007 (2014).
Headrick, M., Hubeny, V. E., Lawrence, A. & Rangamani, M. Causality and holographic entanglement entropy. J. High. Energy Phys.12, 162 (2014).
Headrick, M. Entanglement Rényi entropies in holographic theories. Phys. Rev. D.82, 126010 (2010).
Terhal, B. M., Horodecki, M., Leung, D. W. & DiVincenzo, D. P. The entanglement of purification. J. Math. Phys.43, 4286–4298 (2002).
Bagchi, S. & Pati, A. K. Monogamy, polygamy, and other properties of entanglement of purification. Phys. Rev. A91, 042323 (2015).
Chen, J. & Winter, A. Non-additivity of the entanglement of purification (beyond reasonable doubt). Preprint at https://arxiv.org/abs/1206.1307 (2012).
DiVincenzo, D. P., Horodecki, M., Leung, D. W., Smolin, J. A. & Terhal, B. M. Locking classical correlation in quantum states. Phys. Rev. Lett.92, 067902 (2004).
Horodecki, K., Horodecki, M., Horodecki, P. & Oppenheim, J. Locking entanglement measures with a single qubit. Phys. Rev. Lett.94, 200501 (2005).
Christandl, M. & Winter, A. Uncertainty, monogamy, and locking of quantum correlations. IEEE Trans. Inf. Theory51, 3159–3165 (2005).
Tucci, R. R. Entanglement of distillation and conditional mutual information. Preprint at https://arxiv.org/abs/quant-ph/0202144 (2002).
Christandl, M. & Winter, A. “Squashed entanglement”: An additive entanglement measure. J. Math. Phys.45, 829 (2004).
Vidal, G. Entanglement renormalization. Phys. Rev. Lett.99, 220405 (2007).
Vidal, G. A class of quantum many-body states that can be efficiently simulated. Phys. Rev. Lett.101, 110501 (2008).
Acknowledgements
We thank V. Hubeny, N. Kubo, N. Lashkari, T. Numasawa, H. Ooguri, J. Preskill, M. Rangamani, N. Shiba, T. Ugajin and G. Vidal for useful conversations. We are very grateful to J. Oppenheim for valuable comments on the properties of entanglement of purification. We also thank M. Headrick and H. Maxfield very much for helpful comments on the draft of this article, from which we learned that they had independent ideas on the entanglement wedge cross-section from different perspectives. T.T. is supported by the Simons Foundation through the `It from Qubit' collaboration and by JSPS Grant-in-Aid for Scientific Research (A) no.16H02182. T.T. is also supported by the World Premier International Research Center Initiative (WPI Initiative) from the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT).
Author information
Authors and Affiliations
Contributions
T.T. studied the holographic formula of entanglement wedge cross section and its tensor network interpretation. K.U. identified this with a holographic counterpart of entanglement of purification and showed that the holographic formula reproduces the correct inequalities.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Umemoto, K., Takayanagi, T. Entanglement of purification through holographic duality. Nature Phys 14, 573–577 (2018). https://doi.org/10.1038/s41567-018-0075-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0075-2
This article is cited by
-
Negativity and its capacity in JT gravity
Journal of High Energy Physics (2024)
-
Holographic entanglement distillation from the surface state correspondence
Journal of High Energy Physics (2024)
-
Entanglement islands read perfect-tensor entanglement
Journal of High Energy Physics (2024)
-
Toward random tensor networks and holographic codes in CFT
Journal of High Energy Physics (2023)
-
The Markov gap in the presence of islands
Journal of High Energy Physics (2023)