Multiscale unfolding of real networks by geometric renormalization

Abstract

Symmetries in physical theories denote invariance under some transformation, such as self-similarity under a change of scale. The renormalization group provides a powerful framework to study these symmetries, leading to a better understanding of the universal properties of phase transitions. However, the small-world property of complex networks complicates application of the renormalization group by introducing correlations between coexisting scales. Here, we provide a framework for the investigation of complex networks at different resolutions. The approach is based on geometric representations, which have been shown to sustain network navigability and to reveal the mechanisms that govern network structure and evolution. We define a geometric renormalization group for networks by embedding them into an underlying hidden metric space. We find that real scale-free networks show geometric scaling under this renormalization group transformation. We unfold the networks in a self-similar multilayer shell that distinguishes the coexisting scales and their interactions. This in turn offers a basis for exploring critical phenomena and universality in complex networks. It also affords us immediate practical applications, including high-fidelity smaller-scale replicas of large networks and a multiscale navigation protocol in hyperbolic space, which betters those on single layers.

Main

The definition of self-similarity and scale invariance^1,2 in complex networks has been limited by the lack of a valid source of geometric length-scale transformations. Previous efforts to study these symmetries are based on topology and include spectral coarse-graining³ or box-covering procedures based on shortest path lengths between nodes^4,5,6,7,8,9. However, the collection of shortest paths is a poor source of length-based scaling factors in networks due to the small-world¹⁰ or even ultrasmall-world¹¹ properties, and the problem remained open. Other studies have approached the multiscale structure of network models in a more geometric way^12,13, but their findings cannot be directly applied to real-world networks.

Models of complex networks based on hidden metric spaces^14,15,16,17 open the door to a proper geometric definition of self-similarity and scale invariance and to an unfolding of the different scales present in the structure of real networks. These models are able to explain universal features shared by real networks—including the small-world property, scale-free degree distributions and clustering—and also fundamental mechanisms, such as preferential attachment in growing networks¹⁸ and the emergence of communities¹⁹.

Naturally, the geometricalization of networks allows a reservoir of distance scales so that we can borrow concepts and techniques from the renormalization group in statistical physics^20,21. By recursive averaging over short-distance degrees of freedom, renormalization has successfully explained, for instance, the universality properties of critical behaviour in phase transitions²². In this study, we introduce a geometric renormalization group for complex networks (RGN). The method, inspired by the block spin renormalization group devised by L. P. Kadanoff²⁰, relies on a geometric embedding of the networks to coarse-grain neighbouring nodes into supernodes and to define a new map that progressively selects long-range connections.

Evidence of geometric scaling in real networks

Hidden metric space network models couple the topology of a network to an underlying geometry through a universal connectivity law depending on distances on such space, which combine popularity and similarity dimensions^14,17,18, such that more popular and similar nodes have more chance to interact. Popularity is related to the degrees of the nodes^14,23, and similarity stands as an aggregate of all other attributes that modulate the likelihood of interactions. These two dimensions define a hyperbolic plane as the effective geometry of networks, and their contribution to the probability of connection can be explicit or combined into an effective hyperbolic distance. This gives rise to the two isomorphic geometric models, ${{\mathbb{S}}}^{1}$ and ${{\mathbb{H}}}^{2}$. In the ${{\mathbb{S}}}^{1}$ model¹⁴, the popularity of a node i is associated with a hidden degree κ_i, complemented by its angular position in the one-dimensional sphere (or circle) as a similarity measure, such that the probability of connection increases with the product of the hidden degrees and decreases with their distance along the circle (equation (5) in Methods). Reciprocally, in the equivalent ${{\mathbb{H}}}^{2}$ model^16,17, the hidden degree is transformed into a radial coordinate, such that higher degree nodes are placed closer to the centre of the hyperbolic disk, while the angular coordinate remains as in the ${{\mathbb{S}}}^{1}$ circle, and the probability of connection decreases with the hyperbolic distance. In their scale-free version, both models have only three parameters μ, γ and β, which control the average degree $\left\langle k\right\rangle$, the exponent of the degree distribution γ and the local clustering coefficient $\bar{c}$, respectively. The radius R of the ${{\mathbb{S}}}^{1}$ circle is adjusted to maintain a constant density of nodes equal to one.

The renormalization transformation is defined on the basis of the similarity dimension represented by the angular coordinate of the nodes. We present here the formulation for the ${{\mathbb{S}}}^{1}$ model, as it makes the similarity dimension explicit and is mathematically more tractable. The transformation zooms out by changing the minimum length scale from that of the original network to a larger value. It proceeds by, first, defining non-overlapping blocks of consecutive nodes of size r along the circle and, second, by coarse-graining the blocks into supernodes. Each supernode is then placed within the angular region defined by the corresponding block so that the order of nodes is preserved. All the links between some node in one supernode and some node in the other, if any, are renormalized into a single link between the two supernodes. This operation can be iterated starting from the original network at layer l = 0. Finally, the set of renormalized network layers l, each r^l times smaller than the original one, forms a multiscale shell of the network. Figure 1 illustrates the process.

Fig. 1: Geometric renormalization transformation for complex networks.

Each layer is obtained after a renormalization step with resolution r starting from the original network in l = 0. Each node i in red is placed at an angular position ${\theta }_{i}^{(l)}$ on the ${{\mathbb{S}}}^{1}$ circle and has a size proportional to the logarithm of its hidden degree ${\kappa }_{i}^{(l)}$. Straight solid lines represent the links in each layer. Coarse-graining blocks correspond to the blue shadowed areas, and dashed lines connect nodes to their supernodes in layer l + 1. Two supernodes in layer l + 1 are connected if and only if, in layer l, some node in one supernode is connected to some node in the other (blue links give an example). The geometric renormalization transformation has Abelian semigroup structure with respect to the composition, meaning that a certain number of iterations of a given resolution are equivalent to a single transformation of higher resolution. For instance, in the figure, the same transformation with r = 4 goes from l = 0 to l = 2 in a single step. Whenever the number of nodes is not divisible by r, the last supernode in a layer contains less than r nodes, as in the example at l = 1. The RGN transformations are valid for uneven supernode sizes as well; one could divide the circle into equally sized sectors of a certain arc length such that they contain on average a constant number of nodes. The set of transformations parametrized by r does not include an inverse element to reverse the process.

In this study, we apply the RGN to eight different real scale-free networks from very different domains: technology (Internet²⁴), transportation (Airports^25,26), biology (Metabolic²⁷, Proteome²⁸ and Drosophila²⁹), social (Enron^30,31) and languages (Music³² and Words³³) (section I in the Supplementary Information). First, their geometric maps are obtained by embedding the nodes in the underlying geometry using statistical inference techniques, which identify the hidden degrees and angular coordinates, maximizing the likelihood that the topology of the network is reproduced by the model^15,34. Second, we apply the coarse-graining by defining blocks of size r = 2, and iterate the process. In the limit N → ∞, where N is the number of nodes, the RGN can be applied up to any desired scale of observation, whereas it is bounded to order ${\mathscr{O}}({\rm{log}}N)$ iterations in finite systems.

The resulting topological features of three of the renormalized networks are shown in Fig. 2 (see Supplementary Fig. 1 for the others). We observe that the degree distributions, degree–degree correlations, clustering spectra and community structures (see Methods) show self-similar behaviour. The last property suggests a new and efficient multiscale community detection algorithm for complex networks^35,36,37.

Fig. 2: Self-similarity of real networks along the RGN flow.

Each column shows the RGN flow with r = 2 of different topological features of the Internet autonomous systems (AS) network (left), the human Metabolic network (middle) and the Music network (right). a, Complementary cumulative distribution P_c of rescaled degrees ${k}_{{\rm{res}}}^{(l)}={k}^{(l)}{\rm{/}}\left\langle {k}^{(l)}\right\rangle$. b, Degree-dependent clustering coefficient over rescaled-degree classes. Degree–degree correlations, as measured by the normalized average nearest-neighbour degree ${\bar{k}}_{{\rm{nn,n}}}\left({k}_{{\rm{res}}}^{(l)}\right)={\bar{k}}_{{\rm{nn}}}\left({k}_{{\rm{res}}}^{(l)}\right)\left\langle {k}^{(l)}\right\rangle {\rm{/}}\left\langle {\left({k}^{(l)}\right)}^{2}\right\rangle$, are shown in the insets. c, RGN flow of the community structure. Q^(l) is the modularity in layer l, Q^(l,0) is the modularity that the community structure of layer l induces in the original network and nMI^(l,0) is the normalized mutual information between the latter and the community structure detected directly in the original network (see Methods). The number of layers in each system is determined by their original size. The horizontal dashed lines indicate the modularity in the original networks.

Geometric renormalization of the ${{\mathbb{S}}}^{1}{\rm{/}}{{\mathbb{H}}}^{2}$ model

The self-similarity exhibited by real-world networks can be understood in terms of their congruency with the hidden metric space network model. As we show analytically, the ${{\mathbb{S}}}^{1}$ and ${{\mathbb{H}}}^{2}$ models are renormalizable in a geometric sense. This means that if a real scale-free network is compatible with the model and admits a good embedding, as it is the case for the real networks analysed in this study, the model will be able to predict its self-similarity and geometric scaling.

We demonstrate next the renormalizability of the ${{\mathbb{S}}}^{1}$ model (see section II in the Supplementary Information for mathematical details and also for the definition of the RGN in hyperbolic space). The renormalized networks remain maximally congruent with the hidden metric space model by assigning a new hidden degree ${\kappa }_{i}^{(l+1)}$ to supernode i in layer l + 1 as a function of the hidden degrees of the nodes it contains in layer l according to:

$${\kappa }_{i}^{(l+1)}={\left(\sum _{j=1}^{r}{\left({\kappa }_{j}^{(l)}\right)}^{\beta }\right)}^{1/\beta }$$

(1)

as well as an angular coordinate ${\theta }_{i}^{(l+1)}$ given by:

$${\theta }_{i}^{(l+1)}={\left(\frac{\sum _{j=1}^{r}{\left({\theta }_{j}^{(l)}{\kappa }_{j}^{(l)}\right)}^{\beta }}{\sum _{j=1}^{r}{\left({\kappa }_{j}^{(l)}\right)}^{\beta }}\right)}^{1/\beta }$$

(2)

The global parameters need to be rescaled as μ^(l+1) = μ^(l)/r, β^(l+1) = β^(l), and R^(l+1) = R^(l)/r. This implies that the probability ${p}_{ij}^{(l+1)}$ for two supernodes i and j to be connected in layer l + 1 maintains its original form (equation (5) and Fig. 3a). This applies both to the model and to real networks as long as they admit a good embedding (Supplementary Fig. 2). In addition, notice that the renormalization transformations of the geometric layout also have the Abelian semigroup structure.

Fig. 3: RGN flow of synthetic and real networks.

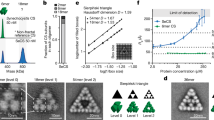
a, Empirical connection probability (p) in a synthetic ${{\mathbb{S}}}^{1}$ network. Fraction of connected pairs of nodes as a function of ${\chi }_{ij}^{(l)}={R}^{(l)}{\rm{\Delta }}{\theta }_{ij}^{(l)}{\rm{/}}\left({\mu }^{(l)}{\kappa }_{i}^{(l)}{\kappa }_{j}^{(l)}\right)$ in the renormalized layers, from l = 0 to l = 8, and r = 2. The original synthetic network has N ≅ 225,000 nodes, γ = 2.5 and β = 1.5. The black dashed line shows the theoretical curve (equation (5)). The inset shows the invariance of the mean local clustering along the RGN flow. b, Hyperbolic embedding of the Metabolic network (top) and its renormalized layer l = 2 (bottom). The colours of the nodes correspond to the community structure detected by the Louvain algorithm. Notice how the renormalized network preserves the original community structure despite being four times smaller. c, Real networks in the connectivity phase diagram. The synthetic network above is also shown. Darker blue (green) in the shaded areas represent higher values of the exponent ν. The dashed line separates the γ-dominated region from the β-dominated region. In phase I, ν > 0 and the network flows towards a fully connected graph. In phase II, ν < 0 and the network flows towards a one-dimensional ring. The red thick line indicates ν = 0 and, hence, the transition between the small-world and non-small-world phases. In region III, the degree distribution loses its scale-freeness along the flow. The inset shows the exponential increase of the average degree of the renormalized real networks $\left\langle {k}^{(l)}\right\rangle$ with respect to l.

As the networks remain congruent with the ${{\mathbb{S}}}^{1}$ model, hidden degrees κ^(l) remain proportional to observed degrees k^(l), which allows us to explore the degree distribution of the renormalized layers analytically. It can be shown that, if the original distribution of hidden degrees is a power law with characteristic exponent γ, the renormalized distribution is also a power law with the same exponent asymptotically, as long as (γ − 1)/2 < β (section II in the Supplementary Information), with the only difference being the average degree. Interestingly, the global parameter controlling the clustering coefficient, β, does not change along the flow, which explains the self-similarity of the clustering spectra. Finally, the transformation for the angles (equation (2)) preserves the ordering of nodes and the heterogeneity in their angular density and, as a consequence, the community structure is preserved in the flow^15,19,27,38, as shown in Fig. 3b. The model is therefore renormalizable, and RGN realizations at any scale belong to the same ensemble with a different average degree, which should be rescaled to produce self-similar replicas.

A good approximation of the behaviour of the average degree for very large networks can be calculated by taking into account the transformation of hidden degrees along the RGN flow (equation (1) and section II in the Supplementary Information). We obtain ${\left\langle k\right\rangle }^{(l+1)}={r}^{\nu }{\left\langle k\right\rangle }^{(l)}$, with a scaling factor ν depending on the connectivity structure of the original network. If $0 < \frac{\gamma -1}{\beta }\le 1$, the flow is dominated by the exponent of the degree distribution γ, and the scaling factor is given by:

$$\nu =\frac{2}{\gamma -1}-1$$

(3)

whereas the flow is dominated by the strength of clustering if $1\le \frac{\gamma -1}{\beta } < 2$ and

$$\nu =\frac{2}{\beta }-1$$

(4)

Therefore, if γ < 3 or β < 2 (phase I in Fig. 3c), then ν > 0 and the model flows towards a highly connected graph; the average degree is preserved if γ = 3 and β ≥ 2 or β = 2 and γ ≥ 3, which indicates that the network is at the edge of the transition between the small-world and non-small-world phases; and ν < 0 if γ > 3 and β > 2, causing the RGN flow to produce sparser networks approaching a unidimensional ring structure as a fixed point (phase II in Fig. 3c). In this case, the renormalized layers eventually lose the small-world property. Finally, if β < (γ − 1)/2, the degree distribution becomes increasingly homogeneous as r → ∞ (phase III in Fig. 3c), revealing that degree heterogeneity is only present at short scales.

In Fig. 3c, several real networks are shown in the connectivity phase diagram. All of them lay in the region of small-world networks. Furthermore, all of them, except the Internet, Airports and Drosophila networks, belong to the β-dominated region. The inset shows the behaviour of the average degree of each layer l, $\left\langle {k}^{(l)}\right\rangle$; as predicted, it grows exponentially in all cases.

Interestingly, global properties of the model, such as those reflected in the spectrum of eigenvalues of both the adjacency and Laplacian matrices, and quantities such as the diffusion time and the restabilization time³⁹, show a dependence on γ and β, which is in consonance with the one displayed by the RGN flow of the average degree (Supplementary Figs. 10–12). The ${{\mathbb{S}}}^{1}$ model seems to be more sensitive to small changes in degree heterogeneity in the region $0 < \frac{\gamma -1}{\beta }\le 1$, whereas changes in clustering are better reflected when $1\le \frac{\gamma -1}{\beta }\le 2$.

Finally, the RGN transformation can be reformulated for the model in D dimensions. We have recalculated the connectivity phase diagram in Fig. 3c, obtaining qualitatively the same transitions and phases, including region III. Interestingly, the high clustering coefficient observed in real networks poses an upper limit on the potential dimension of the similarity space. We have tested the renormalization transformation using the one-dimensional embedding of networks generated in higher dimensions for which the clustering is realistic, that is, D ≲ 10, and found the same results as in the D = 1 case. The agreement is explained by the fact that the one-dimensional embedding provides a faithful representation for low-dimensional similarity-space networks (section II in the Supplementary Information).

Applications

Next, we propose two specific applications. The first one, the production of downscaled network replicas, singles out a specific scale while the second one, a multiscale navigation protocol, exploits multiple scales simultaneously.

The downscaling of the topology of large real-world complex networks to produce smaller high-fidelity replicas can find useful applications, for instance, as an alternative or guidance to sampling methods in large-scale simulations and, in networked communication systems like the Internet, as a reduced testbed to analyse the performance of new routing protocols^40,41,42,43. Downscaled network replicas can also be used to perform finite size scaling of critical phenomena in real networks, so that critical exponents could be evaluated starting from a single size instance network. However, the success of such programmes is based on the quality of the downscaled versions, which should reproduce not only local properties of the original network but also its mesoscopic structure. We now present a method for their construction that exploits the fact that, under renormalization, a scale-free network remains self-similar and congruent with the underlying geometric model in the whole self-similarity range of the multilayer shell.

The idea is to single out a specific scale after a certain number of renormalization steps. Typically, the renormalized average degree of real networks increases in the flow (see inset in Fig. 3c), so we apply a pruning of links to reduce the density to the level of the original network (see Methods). Basically, we re-adjust the average-degree parameter μ^(l) in the ${{\mathbb{S}}}^{1}$ model and then keep only the renormalized links that are consistent with the readjusted connection probabilities to obtain a statistically equivalent but reduced version.

To illustrate the high-fidelity that downscaled network replicas can achieve, we use them to reproduce the behaviour of dynamical processes in real networks. We selected three different dynamical processes, the classic ferromagnetic Ising model, the susceptible–infected–susceptible (SIS) epidemic spreading model and the Kuramoto model of synchronization (see Methods). We test these dynamics in all the self-similar network layers of the real networks analysed in this study. Results are shown in Fig. 4 and Supplementary Fig. 13. Quite remarkably, for all dynamics and all networks, we observe very similar results between the original and downscaled replicas at all scales. This is particularly interesting as these dynamics have a strong dependence on the mesoscale structure of the underlying networks.

Fig. 4: Dynamics on the downscaled replicas.

Each column shows the order parameters versus the control parameters of different dynamical processes on the original and downscaled replicas of the Internet AS network (left), the human Metabolic network (middle) and the Music network (right) with r = 2, that is, every value of l identifies a network 2^l times smaller than the original one. All points show the results averaged over 100 simulations. Error bars indicate the standard deviations of the order parameters. a, Magnetization ${\left\langle \left|m\right|\right\rangle }^{(l)}$ of the Ising model as a function of the inverse temperature 1/T. b, Prevalence ${\left\langle \rho \right\rangle }^{(l)}$ of the SIS model as a function of the infection rate λ. c, Coherence ${\left\langle r\right\rangle }^{(l)}$ of the Kuramoto model as a function of the coupling strength σ. In all cases, the curves of the smaller-scale replicas are extremely similar to the results obtained on the original networks.

Next, we introduce a new multiscale navigation protocol for networks embedded in hyperbolic space, which improves single-layer results¹⁵. To this end, we exploit the quasi-isomorphism between the ${{\mathbb{S}}}^{1}$ model and the ${{\mathbb{H}}}^{2}$ model in hyperbolic space^16,17 to produce a purely geometric representation of the multiscale shell (see Methods).

The multiscale navigation protocol is based on greedy routing, in which a source node transmitting a packet to a target node sends it to its neighbour closest to the destination in the metric space. As performance metrics, we consider the success rate (fraction of successful greedy paths), and the stretch of successful path (ratio between the number of hops in the greedy path and the topological shortest path). Notice that greedy routing cannot guarantee the existence of a successful path among all pairs of nodes; the packet can get trapped into a loop if sent to an already visited node. In this case, the multiscale navigation protocol can find alternative paths by taking advantage of the increased efficiency of greedy forwarding in the coarse-grained layers. When node i needs to send a packet to some destination node j, node i performs a virtual greedy forwarding step in the highest possible layer to find which supernode should be next in the greedy path. Based on this, node i then forwards the packet to its physical neighbour in the real network, which guarantees that it will eventually reach such supernode. The process is depicted in Fig. 5a (full details in Methods). To guarantee navigation inside supernodes, we require an extra condition in the renormalization process and only consider blocks of connected consecutive nodes (a single node can be left alone forming a supernode by itself). Notice that the new requirement does not alter the self-similarity of the renormalized networks forming the multiscale shell nor the congruency with the hidden metric space (section IV in the Supplementary Information).

Fig. 5: Performance of the multiscale navigation protocol in real networks.

a, Illustration of the multiscale navigation protocol. Red arrows show the unsuccessful greedy path in the original layer of a message attempting to reach the target yellow node. Green arrows show the successful greedy path from the same source using both layers. b, Success rate as a function of the number of layers used in the process, computed for 10⁵ randomly selected pairs. c, Average stretch $\left\langle {l}_{{\rm{g}}}{\rm{/}}{l}_{{\rm{s}}}\right\rangle$, where l_g is the topological length of a path found by the algorithm and l_s is the actual shortest path length in the network. d, Relative average load ${\left\langle {\lambda }_{L}^{i}\right\rangle }_{{\rm{Hubs}}}{\rm{/}}{\left\langle {\lambda }_{0}^{i}\right\rangle }_{{\rm{Hubs}}}$ of hubs, where ${\lambda }_{L}^{i}$ is the fraction of successful greedy paths that pass through node i in the multiscale navigation protocol with L renormalized layers. The averages are computed over the 20 highest-degree nodes in the network.

Figure 5b shows the increase of the success rate as the number of renormalized layers L used in the navigation process is increased for the different real networks considered in this study. Interestingly, the success rate always increases, even in systems with very high navigability in l = 0 like the Internet, and this improvement increases the stretch of successful paths only mildly (Fig. 5c). Counterintuitively, the slight increase of the stretch reduces the burden on highly connected nodes (Fig. 5d). As the number of renormalized layers L increases, the average fraction of successful paths passing through the most connected hubs in the network decreases. The improvements come at the expense of adding information about the supernodes to the knowledge needed for standard greedy routing in single-layered networks. However, the trade-off between improvement and information overload is advantageous, as for many systems the addition of just one or two renormalized layer produces already a notable effect.

Discussion

It is a very well stablished empirical fact that most real complex networks share a very special set of universal features. Among the most relevant ones, networks have heterogeneous degree distributions, strong clustering and are small world. Our hidden metric space network model^14,17,18, independent of its ${{\mathbb{S}}}^{1}$ or ${{\mathbb{H}}}^{2}$ formulation, provides a very natural explanation of these properties with a very limited number of parameters and using an effective hyperbolic geometry of two dimensions. Even if the model and the renormalization group can be formulated in D dimensions, the high clustering coefficient observed in real networks poses an upper limit on the potential dimension of the similarity space so that networks can be faithfully embedded in the one-dimensional representation. This is in line with the accumulated empirical evidence, which unambiguously supports the one-dimensional similarity plus degrees as an extremely good proxy for the geometry of real networks.

Interestingly, the existence of a metric space underlying complex networks allows us to define a geometric renormalization group that reveals their multiscale nature. Our geometric models of scale-free networks are shown to be self-similar under the RGN transformation. Even more important is the finding that self-similarity under geometric renormalization is a ubiquitous symmetry of real-world scale-free networks, which provides new evidence supporting the hypothesis that hidden metric spaces underlie real networks.

The renormalization group presented in this work is similar in spirit to the topological renormalization studied in refs ^4,5,6,7,8,9 and should be taken as complementary. Instead of using shortest paths as a source of length scales to explore the fractality of networks, we use a continuum geometric framework that allows us to unveil the role of degree heterogeneity and clustering in the self-similarity properties of networks. In our model, a crucial point is the explicit contribution of degrees to the probability of connection, allows us to produce both short-range and long-range connections using a single mechanism captured in a universal connectivity law. The combination of similarity with degrees is a necessary condition to make the model predictive of the multiscale properties of real networks.

From a fundamental point of view, the geometric renormalization group introduced here has proven to be an exceptional tool to unravel the global organization of complex networks across scales and promises to become a standard methodology to analyse real complex networks. It can also help in areas such as the study of metapopulation models, in which transportation fluxes or population movements occur on both local and global scales⁴⁴. From a practical point of view, we envision many applications. In large-scale simulations, downscaled network replicas could serve as an alternative or guidance to sampling methods, or for fast-track exploration of rough parameter spaces in the search of relevant regions. Downscaled versions of real networks could also be applied to perform finite size scaling, which would allow for the determination of critical exponents from single snapshots of their topology. Other possibilities include the development of a new multilevel community detection method^45,46,47 that would exploit the mesoscopic information encoded in the different observation scales.

Methods

Renormalization flow of the community structure

To asses how the community structure of the network changes with the RGN flow, we obtained a partition into communities of every layer l, P^(l), using the Louvain method⁴⁸; Fig. 2c shows their modularities Q^(l). We also defined the partition induced by P^(l) on the original network, P^(l,0), obtained by considering that two nodes i and j of the original network are in the same community in P^(l,0) if and only if the supernodes of i and j in layer l belong to the same community in P^(l). Both the modularity Q^(l,0) of P^(l,0) and the normalized mutual information nMI^(l,0) between both partitions P⁽⁰⁾ and P^(l,0) are shown in Fig. 2c.

Connection probability in the ${{\mathbb{S}}}^{1}{\rm{/}}{{\mathbb{H}}}^{2}$ geometric model

The ${{\mathbb{S}}}^{1}$ model¹⁴ places the nodes of a network into a one-dimensional sphere of radius R and connects every pair i, j with probability

$${p}_{ij}=\frac{1}{1+{\chi }_{ij}^{\beta }}=\frac{1}{1+{\left(\frac{{d}_{ij}}{\mu {\kappa }_{i}{\kappa }_{j}}\right)}^{\beta }}$$

(5)

where μ controls the average degree of the network, β its clustering, and d_ij = RΔθ_ij is the distance between the nodes separated by an angle Δθ_ij; R is, without loss of generality, always set to N/2π, where N is the number of nodes, so that the density of nodes along the circle is equal to 1. The hidden degrees κ_i and κ_j are proportional to the degrees of nodes i and j, respectively.

The ${{\mathbb{S}}}^{1}$ model is isomorphic to a purely geometric model, the ${{\mathbb{H}}}^{2}$ model¹⁷, in which nodes are placed in a two-dimensional hyperbolic disk of radius:

$${R}_{{{\mathbb{H}}}^{2}}=2{\rm{ln}}\left(\frac{2R}{\mu {\kappa }_{0}^{2}}\right)$$

(6)

where κ₀ = min{κ_i}. By mapping every mass κ_i to a radial coordinate r_i according to:

$${r}_{i}={R}_{{{\mathbb{H}}}^{2}}-2{\rm{ln}}\frac{{\kappa }_{i}}{{\kappa }_{0}}$$

(7)

the connection probability, equation (5), becomes

$${p}_{ij}=\frac{1}{1+{e}^{\frac{\beta }{2}\left({x}_{ij}-{R}_{{{\mathbb{H}}}^{2}}\right)}}$$

(8)

where ${x}_{ij}={r}_{i}+{r}_{j}+2{\rm{ln}}\frac{{\rm{\Delta }}{\theta }_{ij}}{2}$ is a good approximation to the hyperbolic distance between two points with coordinates (r_i, θ_i) and (r_j, θ_j) in the native representation of hyperbolic space. The exact hyperbolic distance ${d}_{{{\mathbb{H}}}^{2}}$ is given by the hyperbolic law of cosines:

$${d}_{{{\mathbb{H}}}^{2}}={\rm{acosh}}\left({\rm{\cosh }}{r}_{i}{\rm{\cosh }}{r}_{j}-{\rm{\sinh }}{r}_{i}{\rm{\sinh }}{r}_{j}{\rm{\cos }}{\rm{\Delta }}{\theta }_{ij}\right)$$

(9)

Adjusting the average degree of downscaled network replicas

To reduce the average degree in a renormalized network to the level of the original network, we apply a pruning of links using the underlying metric model with which the networks in all layers are congruent. The procedure is detailed in this section.

The renormalized network in layer l has an average degree $\left\langle {k}^{(l)}\right\rangle$ generally larger (in phase I) from the original network’s $\left\langle {k}^{(0)}\right\rangle$. Moreover, the new network is congruent with the underlying hidden metric space with a parameter μ^(l) = μ⁽⁰⁾/r^l controlling its average degree. The main idea is to decrease the value of μ^(l) to a new value ${\mu }_{{\rm{new}}}^{(l)}$—which implies that the connection probability of every pair of nodes (i,j), ${p}_{ij}^{(l)}$, decreases to ${p}_{ij,{\rm{new}}}^{(l)}$. We then prune the existing links by keeping them with probability

$${q}_{ij}^{(l)}=\frac{{p}_{ij,{\rm{new}}}^{(l)}}{{p}_{ij}^{(l)}}$$

(10)

Therefore, the probability for a link to exist in the pruned network reads:

$$P\left\{{a}_{ij,{\rm{new}}}^{(l)}=1\right\}={p}_{ij}^{(l)}{q}_{ij}^{(l)}={p}_{ij,{\rm{new}}}^{(l)}$$

(11)

whereas the probability for it not to exist is:

$$P\left\{{a}_{ij,{\rm{new}}}^{(l)}=0\right\}=1-{p}_{ij}^{(l)}+{p}_{ij}^{(l)}\left(1-{q}_{ij}^{(l)}\right)=1-{p}_{ij,{\rm{new}}}^{(l)}$$

(12)

that is, the pruned network has a lower average degree and is also congruent with the underlying metric space model with the new value of ${\mu }_{{\rm{new}}}^{(l)}$. Hence, we only need to find the right value of ${\mu }_{{\rm{new}}}^{(l)}$ so that $\left\langle {k}_{new}^{(l)}\right\rangle =\left\langle {k}^{(0)}\right\rangle$. In the thermodynamic limit, the average degree of an ${{\mathbb{S}}}^{1}$ network is proportional to μ, so we could simply set

$${\mu }_{{\rm{new}}}^{(l)}=\frac{\left\langle {k}^{(0)}\right\rangle }{\left\langle {k}^{(l)}\right\rangle }{\mu }^{(l)}$$

(13)

However, as we consider real-world networks, finite-size effects play an important role. Indeed, we need to correct the value of ${\mu }_{{\rm{new}}}^{(l)}$ in equation (13). To this end, we use a correcting factor c, initially set to c = 1, and use ${\mu }_{{\rm{new}}}^{(l)}=c\frac{\left\langle {k}^{(0)}\right\rangle }{\left\langle {k}^{(l)}\right\rangle }{\mu }^{(l)}$; for every value of c, we prune the network. If $\left\langle {k}_{{\rm{new}}}^{(l)}\right\rangle > \left\langle {k}^{(0)}\right\rangle$, we give c the new value c − 0.1u → c, where u is a random variable uniformly distributed between 0 and 1. Similarly, if $\left\langle {k}_{{\rm{new}}}^{(l)}\right\rangle < \left\langle {k}^{(0)}\right\rangle$, c + 0.1u → c. The process ends when $\left|\left\langle {k}_{{\rm{new}}}^{(l)}\right\rangle -\left\langle {k}^{(0)}\right\rangle \right|$ is below a given threshold (in our case, we set it to 0.1).

Simulation of dynamical processes

The Ising model is an equilibrium model of interacting spins⁴⁹. Every node i is assigned a variable s_i with two possible values s_i = ±1, and the energy of the system is, in the absence of external field, given by the Hamiltonian

$${\mathscr{H}}=-\sum _{i < j}{J}_{ij}{a}_{ij}{s}_{i}{s}_{j}$$

(14)

where a_ij are the elements of the adjacency matrix and J_ij are coupling constants, which we set to one. We start from an initial condition with s_i = 1 for all i and explore the ensemble of configurations using the Metropolis-Hastings algorithm: we randomly select one node and propose a change in its spin, −s_i → s_i. If ${\rm{\Delta }}{\mathscr{H}}\le 0$, we accept the change; otherwise, we accept it with probability ${e}^{-{\rm{\Delta }}{\mathscr{H}}{\rm{/}}T}$, where T is the temperature acting as a control parameter. The order parameter is the absolute magnetization per spin $\left|m\right|$, where $m=\frac{1}{N}{\sum }_{i}{s}_{i}$; if all spins point in the same direction, $\left|m\right|=1$, whereas $\left|m\right|=0$ if half the spins point in each direction.

In the SIS dynamical model of epidemic spreading⁵⁰, every node i can present two states at a given time t, susceptible (n_i(t) = 0) or infected (n_i(t) = 1). Both infection and recovery are Poisson processes. An infected node recovers with rate 1, whereas infected nodes infect their susceptible neighbours at rate λ. We simulate this process using the continuous-time Gillespie algorithm with all nodes initially infected. The order parameter is the prevalence or fraction of infected nodes $\rho (t)=\frac{1}{N}{\sum }_{i}{n}_{i}(t)$.

The Kuramoto model is a dynamical model for coupled oscillators. Every node i is described by a natural frequency ω_i and a time-dependent phase θ_i(t). A node’s phase evolves according to:

$${\mathop{\theta }\limits^{^\circ }}_{i}={\omega }_{i}+\sigma \sum _{i < j}{a}_{ij}{\rm{\sin }}({\theta }_{j}(t)-{\theta }_{i}(t))$$

(15)

where a_ij are the adjacency matrix elements and σ is the coupling strength. We integrate the equations of motion using Heun’s method. Initially, the phases θ_i(0) and the frequencies ω_i are randomly drawn from the uniform distributions U(−π, π) and U(−1/2, 1/2) respectively, as in ref. ⁵¹. The order parameter $r(t)=\frac{1}{N}\left|{\sum }_{i}{e}^{i{\theta }_{i}(t)}\right|$ measures the phase coherence of the set of nodes; if all nodes oscillate in phase, r(t) = 1, whereas r(t) → 0 if nodes oscillate in a disordered manner.

In every realization, we compute an average of the order parameter in the stationary state. In the case of the SIS model, the single-realization mean of prevalence values is weighted by time. The curves presented in this work correspond to statistics over 100 realizations.

Multiscale navigation

Given a network and its embedding (layer 0), we merge pairs of consecutive nodes only if they are connected, which guarantees navigation inside supernodes; this process generates layer 1. We repeat the process to generate L renormalized layers. The multiscale navigation protocol requires every node i to be provided with the following local information:

• 1. The coordinates $\left({r}_{i}^{(l)},{\theta }_{i}^{(l)}\right)$ of node i in every layer l.

• 2. The list of (super)neighbours of node i in every layer as well as their coordinates.

• 3. Let SuperN(i, l) be the supernode to which i belongs in layer l. If SuperN(i, l) is connected to SuperN(k, l) in layer l, at least one of the (super)nodes in layer l − 1 belonging to SuperN(i, l) must be connected to at least one of the (super)nodes in layer l − 1 belonging to SuperN(k, l); such node is called 'gateway'. For every superneighbour of node SuperN(i, l) in layer l, node i knows which (super)node or (super)nodes in layer l − 1 are gateways reaching it. Notice that both the gateways and SuperN(i,l − 1) belong to SuperN(i, l) in layer l so, in layer l − 1, they must either be the same (super)node or different but connected (super)nodes.

• 4. If SuperN(i, l − 1) is a gateway reaching some supernode s, at least one of its (super)neighbours in layer l − 1 belongs to s; node i knows which.

This information allows us to navigate the network as follows. Let j be the destination node to which i wants to forward a message, and let node i know j’s coordinates in all L layers $\left({r}_{j}^{(l)},{\theta }_{j}^{(l)}\right)$. To decide which of its physical neighbours (that is, in layer 0) should be next in the message-forwarding process, node i must first check if it is connected to j; in that case, the decision is clear. If it is not, it must:

• 1. Find the highest layer l_max in which SuperN(i, l_max) and SuperN(j, l_max) still have different coordinates. Set l = l_max.

• 2. Perform a standard step of greedy routing in layer l: find the closest neighbour of SuperN(i, l) to SuperN(j, l). This is the current target SuperT(l).

• 3. While l > 0, look into layer l − 1:

• Set l = l − 1.

• If SuperN(i, l) is a gateway connecting to some (super)node within SuperT(l + 1), node i sets as new current target SuperT(l) its (super)neighbour belonging to SuperT(l + 1) closest to SuperN(j, l).

• Else node i sets as new target SuperT(l) the gateway in SuperN(i, l + 1) connecting to SuperT(l + 1) (its (super)neighbour belonging to SuperN(i, l + 1)).

• 4. In layer l = 0, SuperT(0) belongs to the real network and she is a neighbour of i, so node i forwards the message to SuperT(0).

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.