Abstract
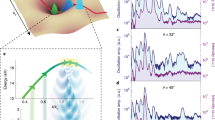
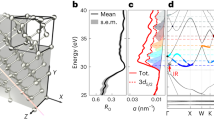
Resolving the fundamental carrier dynamics induced in solids by strong electric fields is essential for future applications, ranging from nanoscale transistors1,2 to high-speed electro-optical switches3. How fast and at what rate can electrons be injected into the conduction band of a solid? Here, we investigate the sub-femtosecond response of GaAs induced by resonant intense near-infrared laser pulses using attosecond transient absorption spectroscopy. In particular, we unravel the distinct role of intra- versus interband transitions. Surprisingly, we found that despite the resonant driving laser, the optical response during the light–matter interaction is dominated by intraband motion. Furthermore, we observed that the coupling between the two mechanisms results in a significant enhancement of the carrier injection from the valence into the conduction band. This is especially unexpected as the intraband mechanism itself can accelerate carriers only within the same band. This physical phenomenon could be used to control ultrafast carrier excitation and boost injection rates in electronic switches in the petahertz regime.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Mei, X. et al. First demonstration of amplification at 1 THz using 25-nm InP high electron mobility transistor process. IEEE Electron Device Lett. 36, 327–329 (2015).
Desai, S. B. et al. MoS2 transistors with 1-nanometer gate lengths. Science 354, 99–102 (2016).
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photon.8, 205–213 (2014).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Mashiko, H., Oguri, K., Yamaguchi, T., Suda, A. & Gotoh, H. Petahertz optical drive with wide-bandgap semiconductor. Nat. Phys.12, 741–745 (2016).
Sommer, A. et al. Attosecond nonlinear polarization and light–matter energy transfer in solids. Nature 534, 86–90 (2016).
Zürch, M. et al. Ultrafast carrier thermalization and trapping in silicon–germanium alloy probed by extreme ultraviolet transient absorption spectroscopy. Struct. Dyn. 4, 044029 (2017).
Zürch, M. et al. Direct and simultaneous observation of ultrafast electron and hole dynamics in germanium. Nat. Commun. 8, 15734 (2017).
Schultze, M. et al. Controlling dielectrics with the electric field of light. Nature 493, 75–78 (2013).
Lucchini, M. et al. Attosecond dynamical Franz–Keldysh effect in polycrystalline diamond. Science 353, 916–919 (2016).
Golde, D., Meier, T. & Koch, S. W. High harmonics generated in semiconductor nanostructures by the coupled dynamics of optical inter- and intraband excitations. Phys. Rev. B 77, 075330 (2008).
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys.7, 138–141 (2011).
Malard, L. M., Mak, K. F., Castro Neto, A. H., Peres, N. M. R. & Heinz, T. F. Observation of intra- and inter-band transitions in the transient optical response of graphene. New J. Phys. 15, 015009 (2013).
Al-Naib, I., Sipe, J. E. & Dignam, M. M. High harmonic generation in undoped graphene: Interplay of inter- and intraband dynamics. Phys. Rev. B 90, 245423 (2014).
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015).
Wismer, M. S., Kruchinin, S. Y., Ciappina, M., Stockman, M. I. & Yakovlev, V. S. Strong-field resonant dynamics in semiconductors. Phys. Rev. Lett. 116, 197401 (2016).
Paasch-Colberg, T. et al. Sub-cycle optical control of current in a semiconductor: from the multiphoton to the tunneling regime. Optica 3, 1358 (2016).
Ludwig, A. et al. Breakdown of the dipole approximation in strong-field ionization. Phys. Rev. Lett. 113, 243001 (2014).
Locher, R. et al. Versatile attosecond beamline in a two-foci configuration for simultaneous time-resolved measurements. Rev. Sci. Instrum. 85, 013113 (2014).
Hentschel, M. et al. Attosecond metrology. Nature 414, 509–513 (2001).
Itatani, J. et al. Attosecond streak camera. Phys. Rev. Lett. 88, 173903 (2002).
Schlaepfer, F. et al. Gouy phase shift for annular beam profiles in attosecond experiments. Opt. Express 25, 3646–3655 (2017).
Beard, M. C., Turner, G. M. & Schmuttenmaer, C. A. Transient photoconductivity in GaAs as measured by time-resolved terahertz spectroscopy. Phys. Rev. B 62, 15764–15777 (2000).
Sato, S. A., Yabana, K., Shinohara, Y., Otobe, T. & Bertsch, G. F. Numerical pump–probe experiments of laser-excited silicon in nonequilibrium phase. Phys. Rev. B 89, 064304 (2014).
Houston, W. V. Acceleration of electrons in a crystal lattice. Phys. Rev. 57, 184–186 (1940).
Srivastava, A., Srivastava, R., Wang, J. & Kono, J. Laser-induced above-band-gap transparency in GaAs. Phys. Rev. Lett. 93, 157401 (2004).
Novelli, F., Fausti, D., Giusti, F., Parmigiani, F. & Hoffmann, M. Mixed regime of light–matter interaction revealed by phase sensitive measurements of the dynamical Franz–Keldysh effect. Sci. Rep. 3, 1227 (2013).
Bakos, J. S. AC stark effect and multiphoton processes in atoms. Phys. Rep. 31, 209–235 (1977).
Vurgaftman, I., Meyer, J. R. & Ram-Mohan, L. R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 89, 5815–5875 (2001).
Kraut, E. A., Grant, R. W., Waldrop, J. R. & Kowalczyk, S. P. Precise determination of the valence-band edge in X-ray photoemission spectra: application to measurement of semiconductor interface potentials. Phys. Rev. Lett. 44, 1620–1623 (1980).
Acknowledgements
We thank M. C. Golling for growing the GaAs, and J. Leuthold and C. Bolognesi for helpful discussion. The authors acknowledge the support of the technology and cleanroom facility at Frontiers in Research: Space and Time (FIRST) of ETH Zurich for advanced micro- and nanotechnology. This work was supported by the National Center of Competence in Research Molecular Ultrafast Science and Technology (NCCR MUST) funded by the Swiss National Science Foundation, and by JSPS KAKENHI grant no. 26-1511.
Author information
Authors and Affiliations
Contributions
F.S., M.L., L.G. and U.K. supervised the study. F.S., M.L., M.V., L.K. and N.H. conducted the experiments. M.V. also improved the experimental set-up and data acquisition system. F.S. fabricated the sample and analysed the experimental data. S.A.S. and A.R. developed the theoretical modelling. All authors were involved in the interpretation and contributed to the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figure 1–13, Supplementary Table 1, Supplementary References
Rights and permissions
About this article
Cite this article
Schlaepfer, F., Lucchini, M., Sato, S.A. et al. Attosecond optical-field-enhanced carrier injection into the GaAs conduction band. Nature Phys 14, 560–564 (2018). https://doi.org/10.1038/s41567-018-0069-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0069-0
This article is cited by
-
Unconventional light - matter interaction in the response-time region of unionized bound electrons
Applied Physics B (2024)
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)
-
Field-driven attosecond charge dynamics in germanium
Nature Photonics (2023)
-
Light-field control of real and virtual charge carriers
Nature (2022)
-
Size-controlled quantum dots reveal the impact of intraband transitions on high-order harmonic generation in solids
Nature Physics (2022)