Abstract
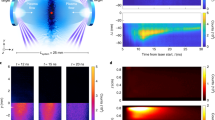
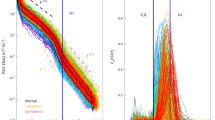
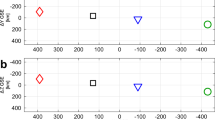
Astrophysical shocks are commonly revealed by the non-thermal emission of energetic electrons accelerated in situ1,2,3. Strong shocks are expected to accelerate particles to very high energies4,5,6; however, they require a source of particles with velocities fast enough to permit multiple shock crossings. While the resulting diffusive shock acceleration4 process can account for observations, the kinetic physics regulating the continuous injection of non-thermal particles is not well understood. Indeed, this injection problem is particularly acute for electrons, which rely on high-frequency plasma fluctuations to raise them above the thermal pool7,8. Here we show, using laboratory laser-produced shock experiments, that, in the presence of a strong magnetic field, significant electron pre-heating is achieved. We demonstrate that the key mechanism in producing these energetic electrons is through the generation of lower-hybrid turbulence via shock-reflected ions. Our experimental results are analogous to many astrophysical systems, including the interaction of a comet with the solar wind9, a setting where electron acceleration via lower-hybrid waves is possible.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Koyama, K. et al. Evidence for shock acceleration of high-energy electrons in the supernova remnant SN1006. Nature 378, 255–258 (1995).
Masters, A. et al. Electron acceleration to relativistic energies at a strong quasi-parallel shock wave. Nat. Phys. 9, 164–167 (2013).
Helder, E. A. et al. Observational signatures of particle acceleration in supernova remnants. Space Sci. Rev. 173, 369–431 (2012).
Blandford, R. & Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 154, 1–75 (1987).
Van Weeren, R. et al. Particle acceleration on megaparsec scales in a merging galaxy cluster. Science 330, 347–349 (2010).
Marcowith, A. et al. The microphysics of collisionless shock waves. Rep. Progress. Phys. 79, 046901 (2016).
Amano, T. & Hoshino, M. Electron injection at high Mach number quasi–perpendicular shocks: Surfing and drift acceleration. Astrophys. J. 661, 190–202 (2007).
Riquelme, M. & Spitkovsky, A. Electron injection by Whistler waves in non-relativistic shocks. Astrophys. J. 733, 63 (2011).
Bingham, R. et al. Generation of X-rays from Comet C/Hyakutake 1996 B2. Science 275, 49–51 (1997).
McClements, K. G. et al. Acceleration of cosmic ray electrons by ion-excited waves at quasiperpendicular shocks. Mon. Not. R. Astron. Soc. 291, 241–249 (1997).
Bingham, R. et al. X-ray emission from comets, cometary knots and supernova remnants. Astrophys. J. 127, 233–237 (2000).
Vink, J. & Laming, M. J. On the magnetic fields and particle acceleration in Cassiopeia A. Astrophys. J. 584, 758–769 (2003).
McBride, J. B. et al. Theory and simulation of turbulent heating by the modified two-stream instability. Phys. Fluids 15, 2367–2382 (1972).
Fisch, N. J. Theory of current drive in plasmas. Rev. Mod. Phys. 59, 175–234 (1987).
Porkolab, M. et al. High-power electron Landau-heating experiments in the lower hybrid frequency range in a tokamak plasma. Phys. Rev. Lett. 53, 1229–1232 (1984).
Cesario, R. et al. Current drive at plasma densities required for thermonuclear reactors. Nat. Commun. 1, 55 (2010).
Eilek, J. A. & Weatherall, J. C. in Diffuse Thermal and Relativistic Plasma in Galaxy Clusters (eds Böhringer, H., Feretti, L. & Schuecker, P.) 71–76 (Max-Planck-Institut fur Extraterrestrische Physik, Garching, 1999).
Cairns, I. H. & Zank, G. P. Turn-on of 2-3 kHz radiation beyond the heliopause. Geophys. Res. Lett. 29, 47-1–47-2 (2002).
Zakharov, Y. P. et al. Simulation of astrophysical plasma dynamics in the laser experiments. AIP Conf. Proc. 369, 357–362 (2008).
Beiersdorfer, P. et al. Laboratory simulation of charge exchange-produced X-ray emission from comets. Science 300, 1558–1559 (2003).
Bell, A. R. et al. Collisionless shock in a laser-produced ablating plasma. Phys. Rev. A. 38, 1363–1369 (1988).
Sagdeev, R. Z. Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23–91 (1966).
Cruz, F. et al. Formation of collisionless shocks in magnetized plasma interaction with kinetic-scale obstacles. Phys. Plasmas 24, 022901 (2017).
Omelchenko, Y. et al. Numerical simulation of quasilinear relaxation of an ion ring and production of superthermal electrons. Sov. J. Plasma Phys 15, 427–431 (1989).
Laming, M. J. Accelerated electrons in Cassiopeia A: thermal and electromagnetic effects. Astrophys. J. 563, 828–841 (2001).
Yamamoto, T. et al. Experimental observation of the rf-driven current by the lower-hybrid wave in a tokamak. Phys. Rev. Lett. 45, 716–719 (1980).
Stenzel, R. L. et al. Electrostatic waves near the lower hybrid frequency. Phys. Rev. A. 11, 2057–2060 (1975).
Boswell, R. W. et al. Very efficient plasma generation by whistler waves near the lower hybrid frequency. Plasma Phys. Control. Fusion 26, 1147 (1984).
Torney, M.et al. Modelling X-ray line and continuum emission from comets. Physica Scr. 2002, T98 (2002)..
Cravens, T. E. et al. Comet Hyakutake X-ray source: Charge transfer of solar wind heavy ions. Geophys. Res. Lett. 24, 105–108 (1997).
Acknowledgements
We thank all the LULI technical staff at École Polytechnique for their support during the experiment. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreements no. 256973 and 247039, AWE plc, the Engineering and Physical Sciences Research Council (grant numbers EP/M022331/1, EP/N014472/1, EP/N013379/1 and EP/N002644/1) and the Science and Technology Facilities Council of the United Kingdom. F.C. and L.O.S. acknowledge support from the European Research Council (InPairs ERC-2015-AdG 695088), FCT Portugal (grant no. PD/BD/114307/2016) the Calouste Gulbenkian Foundation and PRACE for awarding access to resource MareNostrum, based in Spain at the Barcelona Supercomputing Center. The PIC simulations were performed at the IST cluster (Lisbon, Portugal), and MareNostrum (Spain). This work was supported in part at the University of Chicago by the US DOE NNSA ASC through the Argonne Institute for Computing in Science under FWP 57789 and the US DOE Office of Science through grant no. DE- SC0016566. The software used in this work was developed in part by the DOE NNSA ASC- and DOE Office of Science ASCR-supported Flash Center for Computational Science at the University of Chicago.
Author information
Authors and Affiliations
Contributions
G.G., B.R. A.R.B., F.F., S.L., F.M., S.S. and R.Bi. conceived this project, which was designed by G.G., S.L. and M.K. The LULI experiment was carried out by A.R., B.A., J.E.C., Y.H., P.M.K., Y.K., J.R.M., T.M., M.O., Y.S. and M.K. The paper was written by A.R., F.C., B.R. and G.G. The data were analysed by A.R. Numerical simulations were performed by F.C. and P.T. Further experimental and theoretical support was provided by R.Ba., P.G., D.Q.L., C.S., R.T. and L.O.S.
Corresponding author
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary figures 1,2, Supplementary Table 1, Supplementary notes and supplementary references
Rights and permissions
About this article
Cite this article
Rigby, A., Cruz, F., Albertazzi, B. et al. Electron acceleration by wave turbulence in a magnetized plasma. Nature Phys 14, 475–479 (2018). https://doi.org/10.1038/s41567-018-0059-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0059-2
This article is cited by
-
A Case for Electron-Astrophysics
Experimental Astronomy (2022)
-
Laboratory evidence for proton energization by collisionless shock surfing
Nature Physics (2021)
-
Electron acceleration in laboratory-produced turbulent collisionless shocks
Nature Physics (2020)