Abstract
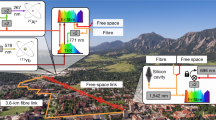
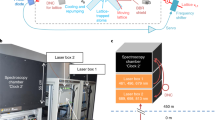
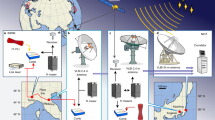
Optical atomic clocks, due to their unprecedented stability1,2,3 and uncertainty3,4,5,6, are already being used to test physical theories7,8 and herald a revision of the International System of Units9,10. However, to unlock their potential for cross-disciplinary applications such as relativistic geodesy11, a major challenge remains: their transformation from highly specialized instruments restricted to national metrology laboratories into flexible devices deployable in different locations12,13,14. Here, we report the first field measurement campaign with a transportable 87Sr optical lattice clock12. We use it to determine the gravity potential difference between the middle of a mountain and a location 90 km away, exploiting both local and remote clock comparisons to eliminate potential clock errors. A local comparison with a 171Yb lattice clock15 also serves as an important check on the international consistency of independently developed optical clocks. This campaign demonstrates the exciting prospects for transportable optical clocks.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Schioppo, M. et al. Ultra-stable optical clock with two cold-atom ensembles. Nat. Photon. 11, 48–52 (2017).
Al-Masoudi, A., Dörscher, S., Häfner, S., Sterr, U. & Lisdat, C. Noise and instability of an optical lattice clock. Phys. Rev. A 92, 063814 (2015).
Nicholson, T. L. et al. Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Commun. 6, 6896 (2015).
Ushijima, I., Takamoto, M., Das, M., Ohkubo, T. & Katori, H. Cryogenic optical lattice clocks. Nat. Photon. 9, 185–189 (2015).
Huntemann, N., Sanner, C., Lipphardt, B., Tamm, C. & Peik, E. Single-ion atomic clock with 3 × 10−18 systematic uncertainty. Phys. Rev. Lett. 116, 063001 (2016).
Chou, C. W., Hume, D. B., Koelemeij, J. C. J., Wineland, D. J. & Rosenband, T. Frequency comparison of two high-accuracy Al+ optical clocks. Phys. Rev. Lett. 104, 070802 (2010).
Huntemann, N. et al. Improved limit on a temporal variation of m p/m e from comparisons of Yb+ and Cs atomic clocks. Phys. Rev. Lett. 113, 210802 (2014).
Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time-variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).
Riehle, F. Towards a redefinition of the second based on optical atomic clocks. C. R. Phys. 16, 506–515 (2015).
Margolis, H. Timekeepers of the future. Nat. Phys. 10, 82–83 (2014).
Vermeer, M. Chronometric levelling. Rep. Finn. Geod. Inst. 83, 2 (1983).
Koller, S. B. et al. Transportable optical lattice clock with 7 × 10−17 uncertainty. Phys. Rev. Lett. 118, 073601 (2017).
Cao, J. et al. A transportable 40Ca+ single-ion clock with 7.7 × 10−17 systematic uncertainty. Appl. Phys. B 123, 112 (2017).
Bongs, K. et al. Development of a strontium optical lattice clock for the SOC mission on the ISS. C. R. Phys. 16, 553–564 (2015).
Pizzocaro, M. et al. Absolute frequency measurement of the 1S0−3P0 transition of 171Yb. Metrologia 54, 102–112 (2017).
Denker, H. in Sciences of Geodesy – II (ed. Xu, G.) Ch. 5 (Springer, 2013).
Lisdat, C. et al. A clock network for geodesy and fundamental science. Nat. Commun. 7, 12443 (2016).
Calonico, D. et al. High-accuracy coherent optical frequency transfer over a doubled 642-km fiber link. Appl. Phys. B 117, 979–986 (2014).
Takano, T. et al. Geopotential measurements with synchronously linked optical lattice clocks. Nat. Photon. 10, 662–666 (2016).
Barwood, G. P. et al. Agreement between two 88Sr+ optical clocks to 4 parts in 1017. Phys. Rev. A 89, 050501 (2014).
Vogt, S. et al. A transportable optical lattice clock. J. Phys. Conf. Ser. 723, 012020 (2016).
Leibrandt, D. R., Bergquist, J. C. & Rosenband, T. Cavity-stabilized laser with acceleration sensitivity below 10−12 g−1. Phys. Rev. A 87, 023829 (2013).
Levi, F. et al. Accuracy evaluation of ITCsF2: a nitrogen cooled caesium fountain. Metrologia 51, 270 (2014).
Grebing, C. et al. Realization of a timescale with an accurate optical lattice clock. Optica 3, 563–569 (2016).
Margolis, H. S. & Gill, P. Least-squares analysis of clock frequency comparison data to deduce optimized frequency and frequency ratio values. Metrologia 52, 628–634 (2015).
Report of the 104 th Meeting of the Comité International des Poids et Mesures (CIPM) (BIPM, 2015).
Nemitz, N. et al. Frequency ratio of Yb and Sr clocks with 5 × 10−17 uncertainty at 150 s averaging time. Nat. Photon-. 10, 258–261 (2016).
Takamoto, M. et al. Frequency ratios of Sr, Yb, and Hg based optical lattice clocks and their applications. C. R. Phys. 16, 489–498 (2015).
Akamatsu, D. et al. Frequency ratio measurement of 171Yb and 87Sr optical lattice clocks. Opt. Express 22, 7898–7905 (2014); erratum 22, 32199–32199 (2014).
Grosche, G. Eavesdropping time and frequency: phase noise cancellation along a time-varying path, such as an optical fiber. Opt. Lett. 39, 2545–2548 (2014).
Katori, H., Takamoto, M., Pal’chikov, V. G. & Ovsiannikov, V. D. Ultrastable optical clock with neutral atoms in an engineered light shift trap. Phys. Rev. Lett. 91, 173005 (2003).
Blatt, S. et al. Rabi spectroscopy and excitation inhomogeneity in a one-dimensional optical lattice clock. Phys. Rev. A 80, 052703 (2009).
Westergaard, P. G. et al. Lattice-induced frequency shifts in Sr optical lattice clocks at the 10−17 level. Phys. Rev. Lett. 106, 210801 (2011).
Middelmann, T., Falke, S., Lisdat, C. & Sterr, U. High accuracy correction of blackbody radiation shift in an optical lattice clock. Phys. Rev. Lett. 109, 263004 (2012).
Safronova, M. S., Porsev, S. G., Safronova, S. U., Kozlov, M. G. & Clark, C. W. Blackbody radiation shift in the Sr optical atomic clock. Phys. Rev. A 87, 012509 (2013).
Sherman, J. A. et al. High accuracy measure of atomic polarizability in an optical lattice clock. Phys. Rev. Lett. 108, 153002 (2012).
JCGM (BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML) Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement Vol. 100 (International Organization for Standardization, 2008); http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf
Voigt, C., Denker, H. & Timmen, L. Time-variable gravity potential components for optical clock comparisons and the definition of international time scales. Metrologia 53, 1365–1383 (2016).
Denker, H. et al. Geodetic methods to determine the relativistic redshift at the level of 10–18 in the context of international timescales—a review and practical results. J. Geod. https://doi.org/10.1007/s00190-017-1075-1 (2017).
Torge, W. & Müller, J. Geodesy 4th edn (De Gruyter, 2012).
European Metrology Research Programme Project SIB-55 International Timescales with Optical Clocks (2016); http://projects.npl.co.uk/itoc/project-structure/reg/gravity-observations/
Mayer-Gürr, T. et al. The combined satellite gravity field model GOCO05s. Geophys. Res. Abstracts 17, EGU2015–12364 (2015).
Barzaghi, R. et al. Orthometric correction and normal heights for Italian levelling network: a case study. Appl. Geomat. 6, 17–25 (2014).
Stenger, J., Schnatz, H., Tamm, C. & Telle, H. R. Ultra-precise measurement of optical frequency ratios. Phys. Rev. Lett. 88, 073601 (2002).
Cox, M. G., Eiø, C., Mana, G. & Pennecchi, F. The generalized weighted mean of correlated quantities. Metrologia 43, S268 (2006).
Boyd, M. M. et al. 87Sr lattice clock with inaccuracy below 10−15. Phys. Rev. Lett. 98, 083002 (2007).
Baillard, X. et al. An optical lattice clock with spin-polarized 87Sr atoms. Eur. Phys. J. D. 48, 11–17 (2008).
Campbell, G. K. et al. The absolute frequency of the 87Sr optical clock transition. Metrologia 45, 539–548 (2008).
Hong, F.-L. et al. Measuring the frequency of a Sr optical lattice clock using a 120 km coherent optical transfer. Opt. Lett. 34, 692–694 (2009).
Falke, S. et al. The 87Sr optical frequency standard at PTB. Metrologia 48, 399–407 (2011).
Yamaguchi, A. et al. Stability transfer between two clock lasers operating at different wavelengths for absolute frequency measurement of clock transition in 87Sr. Appl. Phys. Express 5, 022701 (2012).
Matsubara, K. et al. Direct comparison of a Ca+ single-ion clock against a Sr lattice clock to verify the absolute frequency measurement. Opt. Express 20, 22034–22041 (2012).
Le Targat, R. et al. Experimental realization of an optical second with strontium lattice clocks. Nat. Commun. 4, 2109 (2013).
Falke, S. et al. A strontium lattice clock with 3 × 10−17 inaccuracy and its frequency. New J. Phys. 16, 073023 (2014).
Akamatsu, D. et al. Spectroscopy and frequency measurement of the 87Sr clock transition by laser linewidth transfer using an optical frequency comb. Appl. Phys. Express 7, 012401 (2014).
Hachisu, H. et al. Direct comparison of optical lattice clocks with an intercontinental baseline of 9000 km. Opt. Lett. 39, 4072–4075 (2014).
Lin, Y.-G. et al. First evaluation and frequency measurement of the strontium optical lattice clock at NIM. Chin. Phys. Lett. 32, 090601 (2015).
Tanabe, T. et al. Improved frequency measurement of the 1S0–3P0 clock transition in 87Sr using a Cs fountain clock as a transfer oscillator. J. Phys. Soc. Jpn. 84, 115002 (2015).
Lodewyck, J. et al. Optical to microwave clock frequency ratios with a nearly continuous strontium optical lattice clock. Metrologia 53, 1123 (2016).
Hachisu, H., Petit, G. & Ido, T. Absolute frequency measurement with uncertainty below 1 × 10−15 using International Atomic Time. Appl. Phys. B 123, 34 (2017).
Hachisu, H., Petit, G., Nakagawa, F., Hanado, Y. & Ido, T. SI-traceable measurement of an optical frequency at the low 10−16 level without a local primary standard. Opt. Express 25, 8511–8523 (2017).
Kohno, T. et al. One-dimensional optical lattice clock with a fermionic 171Yb isotope. Appl. Phys. Express 2, 072501 (2009).
Lemke, N. D. et al. Spin-1/2 optical lattice clock. Phys. Rev. Lett. 103, 063001 (2009).
Yasuda, M. et al. Improved absolute frequency measurement of the 171Yb optical lattice clock towards a candidate for the redefinition of the second. Appl. Phys. Express 5, 102401 (2012).
Park, C. Y. et al. Absolute frequency measurement of 1S0 (F = 1/2) mm–3P0 (F = 1/2) transition of 171Yb atoms in a one-dimensional optical lattice at KRISS. Metrologia 50, 119–128 (2013).
Kim, H. et al. Improved absolute frequency measurement of the 171Yb optical lattice clock at KRISS relative to the SI second. Jpn J. Appl. Phys. 56, 050302 (2017).
Acknowledgements
We would like to thank T. Zampieri for his technical support at LSM and A. Mura and Consorzio TOP-IX for technical help in the access to the optical fibre. The authors acknowledge funding from European Metrology Research Program (EMRP) Project SIB55 ITOC, the EU Innovative Training Network (ITN) Future Atomic Clock Technology (FACT), the DFG funded CRC 1128 geo-Q (Projects A03 and C04) and RTG 1728 and the UK National Measurement System Quantum, Electromagnetics and Time Programme. The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union.
Author information
Authors and Affiliations
Contributions
D.C. coordinated the measurement campaign with contributions from C.L., H.S.M. and Mi.Z.; J.G., S.K., S.V., S.H., U.S. and C.L. designed, built and operated the transportable Sr lattice clock; H.D., C.V. and L.T. made the geodetic measurements and calculated the local gravity potential values; A.R., F.N.B. and H.S.M. prepared, characterized and operated the transportable frequency comb; M.P., P.T., B.R., F.B., and D.C. designed, built and operated the Yb lattice clock; G.A.C. and F.L. designed, built and operated the INRIM Cs fountain, C.C. and A.T. designed, characterized and operated the optical fibre link between INRIM and LSM; C.C., P.B. and Ma.Z. operated the frequency comb at INRIM. J.G., C.C., M.P., F.L., A.R., F.N.B., H.S.M., S.K. and C.L. contributed to the data analysis for the ratio and absolute frequency measurement. C.L. wrote the paper with support from H.S.M. and D.C. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Grotti, J., Koller, S., Vogt, S. et al. Geodesy and metrology with a transportable optical clock. Nature Phys 14, 437–441 (2018). https://doi.org/10.1038/s41567-017-0042-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-017-0042-3
This article is cited by
-
A lab-based test of the gravitational redshift with a miniature clock network
Nature Communications (2023)
-
Improved interspecies optical clock comparisons through differential spectroscopy
Nature Physics (2023)
-
Method for Relative Syntonization of Quantum Clocks: Experimental Studies
Measurement Techniques (2023)
-
The MOCAST+ Study on a Quantum Gradiometry Satellite Mission with Atomic Clocks
Surveys in Geophysics (2023)
-
A compact, transportable 1550 nm ultra-stable laser system with Hertz linewidth
Applied Physics B (2023)