Main

The wave dynamics dictating the evolution of quantum states is of utmost importance in both fundamental studies of quantum systems and quantum technological applications. For photons, the evolution of their spatial structure has been the key in a plethora of promising techniques for quantum communication1,2, information processing3,4, simulation5 and metrology6. One particular feature of a converging wave travelling through its focus is the acquisition of an additional phase shift when compared with a collimated beam or a plane wave travelling the same distance. This effect, which is known as the Gouy phase, was first observed and described by Gouy more than a century ago7,8. Although the phenomenon is well established and can be described through methods in physical optics9,10, the Gouy phase continues to be the topic of studies discussing its underlying physical origin by linking it to properties such as the geometry of the focus, geometric phases and the uncertainty principle9,11,12,13,14,15,16,17,18. In addition to the continued interest aiming at providing an intuition for the phenomenon, this phase anomaly is often harnessed to realize tools in optics19,20,21,22.

Despite the Gouy phase being a general wave phenomenon, studies investigating its role in quantum state evolution have been limited to a few matter wave studies23,24,25,26,27 and spatially separated photon pairs28,29. Although these demonstrations use (locally) single quantum systems and thus observe the effect known for classical light waves, more complex quantum states consisting of multiple identical quantum systems (that is, bosonic systems with multiple excitations) have not been studied before. We term the specific phase acquired by such quantum states the quantum Gouy phase.

In general, any phase accrued by a mode of a photonic quantum system leads to a photon-number dependent phase for the quantum state. This means that whereas a single photon or a classical field would acquire a phase ϕ upon propagation, when N-photons occupy the same mode \((\left|N\right\rangle )\), the quantum state is left with N times the same phase, that is, \(\exp (iN\phi )\left|N\right\rangle\)30. This increased phase sensitivity of photon number states is utilized in so-called N00N states, which have garnered popularity due to their potential to push the sensitivity of measurements to what is considered the absolute physical limit31. N00N states can be compactly expressed for two orthogonal modes p and \({p}^{\prime}\) as

$$\left|{{\Psi }}\right\rangle =\frac{1}{\sqrt{2}}\left({\left|N\right\rangle }_{p}{\left|0\right\rangle }_{{p}^{\prime}}-{\left|0\right\rangle }_{p}{\left|N\right\rangle }_{{p}^{\prime}}\right).$$
(1)

Hence, the enhancement in measurement sensitivity is enabled by the phase difference between the two components being N times the phase difference between the underlying modes. More importantly, using such a N00N state configuration allows for the study of the speed-up of the quantum Gouy phase compared with the classical case.

In the present work we describe theoretically how an N-photon number state evolves upon propagation and verify experimentally the speed-up of the quantum Gouy phase with two-photon N00N states through interference in the transverse structure of a bi-photon. We further show that the quantum Gouy phase speed-up can be applied to super-resolving longitudinal displacement measurements using the quantum Fisher information (QFI) formalism and solidifying its link to the uncertainty interpretation of the Gouy phase12. Finally, we show that our results for N-photon states cannot be simulated by classical light with a λ/N wavelength, demonstrating that the often-used effective de Broglie wavelength approach for multi-photon states, although useful in specific cases32,33,34, is not always accurate. As such, our work brings the fundamental wave feature of the Gouy phase to the quantum domain, thereby opening the path to its utilization in quantum technological applications through its unique quantum state manipulation properties.

Probing the quantum Gouy phase

An interferometric measurement scheme can be used to observe the quantum Gouy phase of N-photons. We chose to use the transverse-spatial modes of paraxial light beams as the different arms of the interferometric scheme, where one mode acts as the required reference arm. More specifically, we used Laguerre–Gaussian (LG) modes, which are a family of orthogonal solutions to the paraxial wave equation in cylindrical coordinates35. In the case of a classical monochromatic field, the Gouy phase of these modes evolves as35

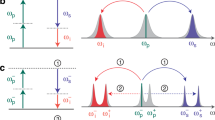
$${{{\Phi }}}_{\mathrm{G}}(z)=-(2p+| \ell | +1)\arctan \left(\frac{2(z-{z}_{0})}{k{w}_{0}^{2}}\right),$$
(2)

where z is the propagation distance, k is the wavenumber, ℓ is an integer giving the number of orbital angular momentum quanta per photon, p is a positive integer defining the radial transverse structure of the field, w0 is the beam waist defining the transverse extent of the beam at its focus, and z0 gives the position of the beam focus along the optical axis. As the Gouy phase depends on the mode order S = 2p + ∣ℓ∣ + 1, its anomalous phase behaviour can be observed through the change of the transverse structure during propagation when the light is in a superposition of spatial modes of different mode orders36. For radial modes, which are LG modes with ℓ = 0, this change results in a varying intensity along the optical axis (as can be seen in Fig. 1a); thus, to probe the quantum Gouy phase and distinguish it from its classical counterpart, we study the superposition of a Gaussian reference mode (p = 0) and different higher-order radial modes in both the classical domain and the aforementioned quantum setting, that is, a N00N state superposition. By measuring the change in intensity and two-photon detection rate, respectively, observed in a single-mode fibre (SMF) scanned through the focus, we are able to directly observe the speed-up of the quantum Gouy phase.

Fig. 1: Observing the quantum Gouy phase through a changing on-axis interference along the propagation direction.
figure 1

a, Conceptual image of the observation scheme. The image displays the intensity structure of a superposition of a radial mode with \(p^{\prime} =4\) and a Gaussian reference (p = 0) at different distances from the focus. The inset shows the intensity of the field on the optical axis. b, Intensity of a classical light beam prepared in the same superposition as in a, with a Gaussian waist w0 = 25 μm and z0 = 0. c, Spatially varying two-photon probability for a two-photon N00N state prepared in the same radial modes as in a and b. To make this structure visible, we post-select for cases in which the two photons exist in the same position using the projection P(x, y, z) = |〈Ψ(z)|2〉x,y|2. For b and c, the intensities/probabilities are calculated on a plane cutting through the optical axis (see a for reference).

Full size image

Theoretical evolution upon propagation

In our measurement scheme, we expect the propagation to result in a photon number-dependent Gouy phase when the state \({\left|N\right\rangle }_{p}\) is translated through a focus. To verify these expectations theoretically, we start with N photons occupying a monochromatic paraxial mode at a position z = 0, with a complex field structure uℓp(ρ, 0). To translate the mode along the optical axis, we apply the translation operator \({\mathrm{e}}^{{{{\rm{i}}}}{\hat{P}}_{z}z/\hslash }\) to the mode in the angular spectrum representation, in which the quantized mode of light can be expressed as

$${\hat{a}}_{\ell p}^{{\dagger} }(0)=\int \int {F}_{\ell p}({{{{\mathbf{ \upkappa}}}}},0){\hat{a}}^{{\dagger} }({{{\mathbf{ \upkappa}}}}){d}^{2}\upkappa \,,$$
(3)

where Fℓp(κ, 0) represents the normalized complex amplitude of the plane wave mode with transverse wave vector κ, and \({\hat{a}}^{{\dagger} }({{{\mathbf{ \upkappa}}}})\) is the corresponding operator density 37,38. After applying the translation operator, the mode takes the form

$${\hat{a}}_{\ell p}^{{\dagger} }(z)=\int \int {F}_{\ell p}({{{\mathbf{ \upkappa}}}},0){\mathrm{e}}^{-{{{\rm{i}}}}{k}_{z}({{{\mathbf{ \upkappa }}}})z}{\hat{a}}^{{\dagger} }({{{\mathbf{ \upkappa}}}}){d}^{2}{\upkappa} \,,$$
(4)

which is identical to the initial mode being propagated by z using the angular spectrum method (ASM)9,39. We thus see that the quantized mode evolves identically to a classical light field, that is, the propagated LG mode has an identical spatial structure uℓp(ρ, z) that only differs by the propagation-related changes to the wavefront curvature and beam radius. Due to the beam evolving according to the ASM, we can extract the Gouy phase evolution by defining a new mode \({\hat{b}}_{\ell p}^{{\dagger} }(z)\)—which has the structure of the field after translation—without the accumulated Gouy phase, that is, \({u}_{\ell p}({{{\mathbf{ \uprho}}}},z){\mathrm{e}}^{-{{{\rm{i}}}}kz}{\mathrm{e}}^{{{{\rm{i}}}}{{{\Phi }}}_{\mathrm{G}}(z)}\). Using this new mode, we can express the mode after propagation as a single mode with a phase

$${\hat{a}}_{\ell p}^{{\dagger} }(z)={\hat{b}}_{\ell p}^{{\dagger} }(z){\mathrm{e}}^{-{{{\rm{i}}}}{{{\Phi }}}_{\mathrm{G}}(z)}\,.$$
(5)

We can then simply state the Gouy phase evolution of an N-photon Fock state as

$${\left|N\right\rangle }_{\ell p;0}\to {\mathrm{e}}^{-{{{\rm{i}}}}Nkz-{{{\rm{i}}}}N{{{\Phi }}}_{\mathrm{G}}(z)}{\left|N\right\rangle }_{\ell p;z}\,,$$
(6)

which explicitly contains the photon number dependent Gouy phase evolution. See Supplementary Section 1 for a detailed derivation.

Experiment

We first prepared laser light in a superposition of the Gaussian reference mode and one of the higher-order radial modes. The structuring of the laser beam was performed with a single hologram on a spatial light modulator (SLM) by using a holographic method commonly known as mode carving40. After structuring, the beam was imaged one focal distance away from a 75 mm lens, which performs an optical Fourier transform on the transverse structure while focusing39. As the transverse structure and its Fourier transform are identical for LG modes, the beam structure at the focus was identical to the structure carved at the SLM, up to a phase factor of π between the superposed LG modes, which needed to be accounted for with odd values of the radial index19,20. To measure the Gouy phase-induced change in the interference along the optical axis, we placed an SMF at the focus and moved it longitudinally using a stage with a computer controlled piezo actuator. The laser source was a continuous-wave diode laser operating at 810 nm and the SLM used for structuring the light was wavefront corrected using the method described in ref. 41. Furthermore, to get the generated modes as close as possible to the correct transverse structure at the desired beam radius, we employed an additional Gaussian correction in the mode carving that minimized any effect of the initial Gaussian beam structure in the carved mode (see Supplementary Section 5).

For a classical field, we can extract the theoretically expected measurement results simply by calculating the overlap of the Gaussian eigenmode of the SMF and the normalized transverse structure of the scalar field \({u}_{{{{\rm{total}}}}}({{{\mathbf{ \uprho}}}},z)\!=\!\frac{1}{\sqrt{2}}({u}_{0p}({{{\mathbf{ \uprho}}}},z)\!-\!{\mathrm{e}}^{{{{\rm{i}}}}\theta }{u}_{0{p}^{\prime}}({{{\mathbf{ \uprho}}}},z)).\) Thus, for laser light, the amount of laser power coupled into the fibre is proportional to

$${P}_{L}\propto {\left|{A}_{p}(z)-{\mathrm{e}}^{-{{{\rm{i}}}}\theta }{A}_{{p}^{\prime}}(z)\right|}^{2},$$
(7)

where Aj(z) refer to the overlap between the normalized radial mode j, at a distance z from its focus, and the normalized Gaussian eigenmode of the fibre. To see the Gouy phase dependence of the detection probability, the above equation can then be stated as

$${P}_{L}\propto [| {A}_{p}{| }^{2}+| {A}_{{p}^{\prime}}{| }^{2}-2| {A}_{p}| | {A}_{{p}^{\prime}}| \cos ({{\Delta }}{{{\Phi }}}_{\mathrm{G}}(z)-\theta +\phi (z))],$$

where the term ϕ(z) is an extra phase contribution from the curvature of the wavefront acquired upon propagation. However, as the wavefront curvature is very small near the optical axis, the only substantial contribution to the phase of the overlaps Aj(z) comes from the Gouy phase difference ΔΦG(z). Thus, scanning the fibre through the focus results in a signal that oscillates as \(\cos \left(2({p}^{\prime}-p)\arctan \left(\frac{2(z-{z}_{0})}{k{w}_{0}^{2}}\right)\right)\) underneath some envelope function defined by the z-dependence of the overlap functions.

For the measurements, we kept the reference mode (that is, a Gaussian mode with radial index p = 0) fixed and varied the index \({p}^{\prime}\) of the probe mode between 1 and 4, which lead to four unique measurement scenarios with differing Gouy-phase contributions. The measured data can be found on the top row of Fig. 2. The measurements follow the probability introduced above very well, which we verified by fitting curves that match equation (7) to the data. In each fit, we fixed the mode field diameter of our fibre to the 5 μm specified by the manufacturer and only had four fitting parameters: an overall scaling factor of the function, the beam waist w0, focal position z0 and the z-independent phase offset θ. The average adjusted R2 value of the fits was 0.986, meaning that the data correspond well with the theoretical model.

Fig. 2: Comparison of on-axis interference along the propagation direction for classical light and two-photon N00N states.
figure 2

The error bars show the mean value ± s.d., solid lines are fits, and the insets show images of the corresponding radial modes with index \({p}^{\prime}\). The upper row contains laser data with 100 repetitions per measurement point, whereas the lower row shows two-photon coincidence measurements. Each two-photon data point was corrected for accidental coincidence detection and measured 25 times with an integration time of 28 s for \({p}^{\prime}=\{1,2,4\}\) and 24 s for \({p}^{\prime}=3\). The fits are nonlinear least-squares fits of the form described in the main text. We aimed to keep the beam waist radius at 25 μm in all measurements to keep the data comparable; however, the fits show that the beam waist was slightly larger for higher-order modes, varying between 24.95 μm and 26.81 μm. A negative stage position labels that the SMF collecting the light was between the focus and the lens.

Source data

Full size image

After first verifying the method’s viability using a laser and showing the effect of the Gouy phase on a classical interference pattern along the optical axis, we extended the measurement scheme to observe the quantum Gouy phase. Following the same general idea, we now generated different two-photon N00N states between a reference Gaussian mode (p = 0) and higher-order radial modes, and studied the two-photon interference pattern along the optical axis. To prepare such a N00N state, we first generated photon pairs through spontaneous parametric down-conversion (see Supplementary Section 5 for more information) and then shaped each of the two photons individually into a well-defined superposition of the wanted radial modes using two holograms performing two different mode carvings. Once each of the photons was structured, we directed the photons into the same beam path using a beamsplitter. As demonstrated in ref. 6, once in the same beam path, indistinguishable photons bunch into the desired spatial mode N00N state given in equation (1). A simplified sketch of the two-photon experimental set-up can be seen in Fig. 3.

Fig. 3: Simplified drawing of the experimental set-up.
figure 3

Two photons with Gaussian beam profiles were sent to separate sections of an SLM where they were independently structured into orthogonal superpositions of radial modes. These photons were then probabilistically overlapped using a beamsplitter, after which they bunched into a radial mode N00N state6. Finally, this two-photon N00N state was focused down to a 25 μm Gaussian beam waist radius and coupled into a SMF (with a mode field diameter of 5 μm) that was scanned through the focus (from behind the focus towards the lens). The two-photons were then probabilistically split into two single-photon avalanche diodes (SPAD), and we post-selected on both of the detectors detecting a photon at the same time using a coincidence counter (CC). See the main text and Supplementary Section 5 for more details.

Source data

Full size image

To calculate the N-photon coincidence probability, we project the radial mode N00N state \(\left|{{\Psi }}(z)\right\rangle\) onto the state where all of the photons have been coupled successfully into the SMF P = ∣〈Ψ(z)∣N〉SMF∣2. Assuming that we produce perfectly balanced N00N states of radial modes with a phase offset θ, the N-photon detection probability can be reduced to the form

$$P=\frac{1}{2}{\left|{A}_{p}^{N}(z)-{\mathrm{e}}^{-{{{\rm{i}}}}\theta }{A}_{{p}^{\prime}}^{N}(z)\right|}^{2}.$$
(8)

As before, we can express this coincidence probability as

$$P=\frac{1}{2}[| {A}_{p}{| }^{2N}+| {A}_{{p}^{\prime}}{| }^{2N}-2| {A}_{p}{| }^{N}| {A}_{{p}^{\prime}}{| }^{N}\cos (N{{\Delta }}{{{\Phi }}}_{\mathrm{G}}-\theta +N\phi (z))],$$

which is similar to the detection probability of the classical field, leading to an oscillating interference underneath some envelope function. However, in the above equation we see the photon number-dependent scaling for both the frequency of the oscillation as well as the envelope term. Note that a probability curve with half the amplitude but the same shape can also be observed for photon pairs prepared similarly without bunching. Thus, to verify that we generate radial mode N00N states in our experiment, we prepared the two photons in the corresponding radial mode superpositions and showed that the probability of coupling both of the photons into the SMF roughly doubles when the photons are made indistinguishable in time, which is a clear signature of bunching (see Supplementary Fig. 2 for the measured data). See Supplementary Sections 2 and 3 for detailed derivations of the detection probabilities.

For the N00N state measurements, we used the same set of radial modes in superposition with the reference Gaussian mode leading to the data shown on the bottom row of Fig. 2. As before, the data follow very well the theoretically expected curves, verifying the above-presented equations and their described behaviours. Fits of equation (8) to the data—with the same parameters as in the classical case—resulted in an average adjusted R2 value of 0.951. The slight imperfections in the data can all be accounted for by imperfections in the alignment, imaging, the SMF eigenmode, spatial mode generation and errors in the stage position. Aside from the errors in the stage positions, all of these can be effectively categorized as contaminations of our state space by modes not included in the theoretical analysis. Hence, our results demonstrate that the quantum Gouy phase leads to a speed up in the accumulated phase upon propagation and also modulates the underlying envelope function. As we will discuss next, both features shed new light on the fundamental understanding of the Gouy phase, as well as hint at quantum enhanced metrology applications.

Quantum Fisher information

As the quantum Gouy phase evolves faster with a larger number of photons, one application could be super-sensitive measurements of longitudinal displacement. This prospect can be investigated by calculating the QFI achieved through translation, which is of the form31,42,43,44

$${F}_{Q}(\left|\psi (z)\right\rangle )=\frac{4}{{\hslash }^{2}}{{{\Delta }}}^{2}{\hat{P}}_{z}{\left|\right.}_{\psi }.$$
(9)

When calculating this variance for the radial mode N00N state \(\left|{{\Psi }}(z)\right\rangle\), we get the QFI

$$\begin{array}{rlr}{F}_{Q}(\left|{{\Psi }}(z)\right\rangle )&=2N\left({{{\Delta }}}^{2}{k}_{z}{| }_{p}+{{{\Delta }}}^{2}{k}_{z}{| }_{{p}^{\prime}}\right)&\\ &+{N}^{2}{\left({\left\langle {k}_{z}\right\rangle }_{p}-{\left\langle {k}_{z}\right\rangle }_{{p}^{\prime}}\right)}^{2},\end{array}$$
(10)

where Δ2kz∣i and \({\left\langle {k}_{z}\right\rangle }_{i}\) are the variance and average of kz for mode i, respectively, calculated using the angular spectrum of the corresponding mode. It is worth noting that the QFI does not depend on z, as the angular spectrum of a mode only acquires a phase structure upon translation. From equation (10), we can see that the second term of the QFI has Heisenberg scaling. As we show in Supplementary Section 4, this term relates to the Gouy phase difference between modes p and \({p}^{\prime}\). Hence, radial mode N00N states along with their quantum Gouy phase properties should be able to enhance the sensitivity of longitudinal displacement measurements. However, although these states provide benefits such as intrinsic interferometric stability when translating the mode along z, the spatial extent of the modes change, making it challenging to devise a real measurement capable of saturating the QFI at any z. The form of equation (10) also shows that it could be possible to engineer different spatially structured quantum states to measure different physical parameters. Due to the form of the QFI, the key feature that needs to be optimized in such state engineering should be maximizing variance of a specific momentum of the quantum state. For example, this would mean maximizing the variance in orbital angular momentum for rotation sensing6 or linear momentum for sensing the longitudinal position (see equation (9)). See Supplementary Section 4 for derivations of the QFI and the Fisher information calculated for the projection used in our experiment.

Momentum uncertainty

In addition to showing the potential for Heisenberg scaling, there is an interesting connection between the QFI and the uncertainty interpretation of the Gouy phase that fundamentally links the potential change in the spread of the transverse momentum to the evolution of the Gouy phase12. Feng and Winful also noted that a larger momentum spread of higher-order modes results in a bigger Gouy phase shift12. As the Gouy phase is increased by the photon number N, which is accompanied by a photon number-dependent momentum spread, as can be seen in equation (10), our results make a further connection between the quantum Gouy phase and its uncertainty interpretation. Similarly to ref. 12, one can further link this behaviour to a tighter spatial confinement of the photons which can be made visible, for example by measuring the spatial extent of the N-photon state as shown in Fig. 1c).

The de Broglie wavelength of light

Finally, our results show that the behaviour of a two-photon N00N state cannot be replicated simply by switching to a classical field with half the wavelength. The difference is clear if we note that the Gouy phase has a nonlinear dependence on the wavenumber, which means that simply ascribing an effective de Broglie wavelength λ/N to the N-photon state does not produce the correct quantum Gouy phase. This is in contrast to the phase accrued by a non-converging field upon propagation as well as arguments discussed in such a context32,33,34. To investigate this fundamental difference in more detail, in Fig. 4 we plotted the measured data for two radial mode N00N states, along with overlap curves calculated for classical 405 nm modes with two different mode orders and waists. From these comparisons we see that the effect is not reproduced by a simple switching of the wavelength or doubling of the mode order.

Fig. 4: Comparing measured two-photon count rates with simulations of classical fields of different wavelength and mode order.
figure 4

a,b, The data shown (black dots) and their fits (grey solid lines) correspond to the two-photon N00N state measurements with probe modes \({p}^{\prime}=3\) (a) and \({p}^{\prime}=4\) (b). The error bars are calculated from 25 repetitions and present the mean value ± s.d. The dashed and dotted lines show simulated values for a 405 nm laser with two different mode orders and beam waists. For the blue dashed curves, the beam radius of the 405 nm field is matched to the 810 nm mode of the photons at the focusing lens. For the red dotted curves, the Rayleigh length is matched to the 810 nm mode while doubling the radial mode order \({p}^{\prime}=\{6,8\}\). Equation (7) with a scaling factor was used to calculate the curves for the classical 405 nm beam and the SMF mode field diameters were scaled to match the change in mode radius (that is, \({w}_{{{{\rm{fibre}}}}}^{405}=\frac{{w}_{0}^{405}}{{w}_{0}^{810}}{w}_{{{{\rm{fibre}}}}}^{810}\)). The curves match well near the focus; however, the blue dashed curve does not exhibit the same fringe pattern and the red dotted curve has a larger relative amplitude outside the focal region. Hence, the quantum Gouy phase behaviour cannot be exactly reproduced by simply changing the wavelength and mode order.

Full size image

Based on the comparison in Fig. 4 and equation (6) the only exact description of the N-photon Fock state evolution seems to be that it evolves as the underlying mode, taken to the power of N. Although doubling the mode order and halving the wavelength seems to replicate quite well the shown two-photon behaviour. As the state evolves as the mode taken to power N, this evolution of the N-photon quantum state results in a more rapid phase change and tighter confinement of the N-photon. Both of these features have been taken advantage of in different studies and experiments. Either in the form of N00N-state super-resolution measurements30,45 or in increasing the confinement46.

Conclusion

In summary, we have verified theoretically and experimentally that the increased phase sensitivity of multi-photon quantum states also extends to the fundamental phase anomaly of converging waves called the Gouy phase. We have shown through single-path interferometric measurements along the optical axis that two-photon N00N states experience twice the Gouy phase when travelling through a focus. As the Gouy phase is a fundamental feature of converging waves, our results should apply broadly to quantum states of any bosonic system. Moreover, as the Gouy phase is an important factor in systems such as optical cavities46,47, and a powerful tool in various applications such as mode sorters and mode converters19,20,21, our results can be widely utilized in applications in quantum optics and quantum information science. In addition to providing a tool for quantum state manipulation, we showed that our results allow Heisenberg-limited scaling in measurements of the longitudinal displacement and, as such, might inspire new superresolution measurement schemes.

Aside from these possible technological applications, we have linked the speed-up of the Gouy phase in the quantum domain to an increased spread in the momentum of an N-photon state. Hence, our results show that the uncertainty interpretation of the phase anomaly12 holds true in the quantum domain. Finally, due to the nonlinear relation between the Gouy phase and the wavenumber, our results unambiguously demonstrate that an N-photon state cannot be rigorously modelled by using a classical field with a wavelength λ/N. However, our results suggest that an additional N-fold increase in the mode order can approximate the effect of the quantum Gouy phase when the beam Rayleigh lengths are matched. This hints at a possible link between an N-photon state and the Nth harmonic of a classical field, which introduces an increase of the mode order and decrease of the beam waist, in addition to doubling the frequency. Thus, our study not only outlines possible applications using the quantum features of spatially structured photons, it also sheds new light on the fundamental understanding of the Gouy phase, a property intrinsic to all systems described by converging or diverging waves.

Methods

Source

The photon pair source uses a 12-mm-long, type-0 periodically poled potassium titanyl phosphate nonlinear crystal that is pumped by a 133.5 mW continuous-wave 405 nm free-space laser. The down-converted photons are filtered through a 3-nm-wide bandpass filter centred around 810 nm, and coupled into separate single-mode fibres. Before the single-mode fibres, one photon is sent through an adjustable delay line. The rate of photon pairs after the single-mode fibres is roughly 3 MHz (correcting for accidentals, efficiency and nonlinearity of detectors).

Spatial mode manipulation

The spatial structures of the photons were modulated with a Holoeye Pluto-2 SLM. To independently shape each photon, a pair of amplitude and phase modulating holograms were displayed on the phase-only SLM. The amplitude modulation was implemented using a method that spatially changes the efficiency of the holograms grating. The N00N states were created by structuring the photons in equal and orthogonal superpositions of the two modes in the N00N state. A detailed figure of the experimental system is shown in the Supplementary Fig. 2 and more experimental details are given in Supplementary Section 5. The Gaussian beam waist of the photon spatial modes was roughly 774 μm before they were focused down to the final SMF (Thorlabs 780HP FC/PC).

Detection

The single-mode fibre to which the final state of light was projected on was scanned around the focus using a translation stage with a computer controlled piezo actuator (Thorlabs PIA13). A coupling stage (xyz-control) and a mount with tip/tilt controls was placed on top of the translation stage to allow maximum control of the alignment of the fibre. As the manufacturer of the piezo actuator stated that the step size of the actuator might differ depending on the direction, the actuator was scanned in the same direction in all measurements. The typical step size provided by the manufacturer (20 nm per piezo step) was used in the data processing. To detect the photon pair, a fibre beamsplitter was used to probabilistically split the photons. Subsequently, two single-photon avalanche photodiodes (Laser Components Count-T) were used in combination with a coincidence counter (IDQ ID900) to post-select for two-photon detections occurring between the two detectors. The coincidence window used to determine coinciding detections was τ = 1 ns and the accidental coincident detections were calculated using the approximate formula R1R2τ, where Ri refer to single photon detection rates in the two detectors. For measuring the coupling efficiency of laser light, two power meters were used. The first one was placed in one output of a fibre beamsplitter, which split the light coming out of the laser into two outputs. The power recorded with this power meter was used to monitor the output power of the laser as a reference signal. The second output of the fibre beamsplitter was fed to the spatial mode manipulation set-up. To record the classical signal, the second power meter was placed directly after the final SMF. The final data is calculated as the power in the second power meter divided by the power in the first one to eliminate the effects of possible laser power fluctuations from the data.