Abstract
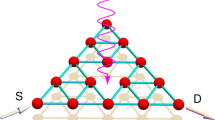
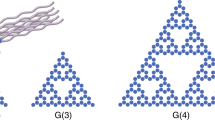
Fractals are fascinating, not only for their aesthetic appeal but also for allowing the investigation of physical properties in non-integer dimensions. In these unconventional systems, many intrinsic features might come into play, including the fractal dimension and the fractal geometry. Despite abundant theoretical studies, experiments in fractal networks remain elusive. Here we experimentally investigate quantum transport in fractal networks by performing continuous-time quantum walks in fractal photonic lattices. We unveil the transport properties through the photon evolution patterns, the mean square displacement and the Pólya number. Contrarily to classical fractals, we observe anomalous transport governed solely by the fractal dimension. In addition, the critical point at which there is a transition from normal to anomalous transport depends on the fractal geometry. Our experiment allows the verification of physical laws in a quantitative manner and reveals the transport dynamics in great detail, thus opening a path to the understanding of more complex quantum phenomena governed by fractality.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Mandelbrot, B. B. Fractals: Form, Chance and Dimension (W. H. Freeman, 1977).
ben-Avraham, D. & Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems (Cambridge Univ. Press, 2000).
Mandelbrot, B. B. The Fractal Geometry of Nature (W. H. Freeman, 1983).
Gouyet, J.-F. Physics and Fractal Structures (Springer, 1996).
Ivanov, P. C. et al. Multifractality in human heartbeat dynamics. Nature 399, 461–465 (1999).
Bandres, M. A., Rechtsman, M. C. & Segev, M. Topological photonic quasicrystals: fractal topological spectrum and protected transport. Phys. Rev. X 6, 011016 (2016).
Tanese, D. et al. Fractal energy spectrum of a polariton gas in a Fibonacci quasiperiodic potential. Phys. Rev. Lett. 112, 146404 (2014).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Brady, R. & Ball, R. Fractal growth of copper electrodeposits. Nature 309, 225–229 (1984).
Goldberger, A. L. et al. Fractal dynamics in physiology: alternations with disease and aging. Proc. Natl Acad. Sci. USA 99, 2466–2472 (2002).
Bassingthwaighte, J. B., Liebovitch, L. S. & West, B. J. Fractal Physiology (Springer, 2013).
Peters, E. E. Fractal structure in the capital markets. Financ. Anal. J. 45, 32–37 (1989).
Dean, C. R. et al. Hofstadteras butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Wang, L. et al. Evidence for a fractional fractal quantum Hall effect in graphene superlattices. Science 350, 1231–1234 (2015).
Benedetti, D. Fractal properties of quantum spacetime. Phys. Rev. Lett. 102, 111303 (2009).
Karman, G., McDonald, G., New, G. & Woerdman, J. Fractal modes in unstable resonators. Nature 402, 138 (1999).
Dudley, J. M., Finot, C., Richardson, D. J. & Millot, G. Self-similarity in ultrafast nonlinear optics. Nat. Phys. 3, 597–603 (2007).
Rivera, J. A., Galvin, T. C., Steinforth, A. W. & Eden, J. G. Fractal modes and multi-beam generation from hybrid microlaser resonators. Nat. Commun. 9, 2594 (2018).
Ding, J., Fan, L., Zhang, S.-Y., Zhang, H. & Yu, W.-W. Simultaneous realization of slow and fast acoustic waves using a fractal structure of Koch curve. Sci. Rep. 8, 1481 (2018).
Fan, J. A. et al. Fractal design concepts for stretchable electronics. Nat. Commun. 5, 3266 (2014).
Fazio, B. et al. Strongly enhanced light trapping in a two-dimensional silicon nanowire random fractal array. Light Sci. Appl. 5, e16062 (2016).
Gottheim, S., Zhang, H., Govorov, A. O. & Halas, N. J. Fractal nanoparticle plasmonics: the Cayley tree. ACS Nano 9, 3284–3292 (2015).
De Nicola, F. et al. Multiband plasmonic Sierpinski carpet fractal antennas. ACS Photonics 5, 2418–2425 (2018).
Zhu, L.-H. et al. Broadband absorption and efficiency enhancement of an ultra-thin silicon solar cell with a plasmonic fractal. Opt. Express 21, A313–A323 (2013).
Havlin, S. & Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 36, 695–798 (1987).
Blumen, A., Klafter, J., White, B. & Zumofen, G. Continuous-time random walks on fractals. Phys. Rev. Lett. 53, 1301 (1984).
Alexander, S. & Orbach, R. Density of states on fractals: fractons. J. Phys. Lett. 43, 625–631 (1982).
Orbach, R. Dynamics of fractal networks. Science 231, 814–819 (1986).
Ben-Avraham, D. & Havlin, S. Diffusion on percolation clusters at criticality. J. Phys. A Math. Gen. 15, L691 (1982).
Sokolov, I. M. What is the alternative to the Alexander–Orbach relation? J. Phys. A Math. Theor. 49, 095003 (2016).
Reis, F. D. A. & Voller, V. R. Models of infiltration into homogeneous and fractal porous media with localized sources. Phys. Rev. E 99, 042111 (2019).
Mülken, O. & Blumen, A. Continuous-time quantum walks: models for coherent transport on complex networks. Phys. Rep. 502, 37–87 (2011).
Agliari, E., Blumen, A. & Mülken, O. Dynamics of continuous-time quantum walks in restricted geometries. J. Phys. A Math. Theor. 41, 445301 (2008).
Darázs, Z., Anishchenko, A., Kiss, T., Blumen, A. & Mülken, O. Transport properties of continuous-time quantum walks on Sierpinski fractals. Phys. Rev. E 90, 032113 (2014).
Volta, A. Quantum walks and trapping on regular hyperbranched fractals. J. Phys. A Math. Theor. 42, 225003 (2009).
van Veen, E., Yuan, S., Katsnelson, M. I., Polini, M. & Tomadin, A. Quantum transport in Sierpinski carpets. Phys. Rev. B 93, 115428 (2016).
Feng, Z. et al. Photonic Newton’s cradle for remote energy transport. Phys. Rev. Appl. 11, 044009 (2019).
Tang, H. et al. Experimental quantum fast hitting on hexagonal graphs. Nat. Photonics 12, 754–758 (2018).
Perets, H. B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).
Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).
Tang, H. et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 4, eaat3174 (2018).
Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52–55 (2007).
Lahini, Y. et al. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 100, 013906 (2008).
Segev, M., Silberberg, Y. & Christodoulides, D. N. Anderson localization of light. Nat. Photonics 7, 197–204 (2013).
Naether, U. et al. Experimental observation of superdiffusive transport in random dimer lattices. New J. Phys. 15, 013045 (2013).
Eichelkraut, T. et al. Mobility transition from ballistic to diffusive transport in non-Hermitian lattices. Nat. Commun. 4, 2533 (2013).
Shang, J. et al. Assembling molecular Sierpiński triangle fractals. Nat. Chem. 7, 389–393 (2015).
Newkome, G. R. et al. Nanoassembly of a fractal polymer: a molecular ‘Sierpinski hexagonal gasket’. Science 312, 1782–1785 (2006).
Rothemund, P. W., Papadakis, N. & Winfree, E. Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol. 2, e424 (2004).
Kempkes, S. N. et al. Design and characterization of electrons in a fractal geometry. Nat. Phys. 15, 127–131 (2019).
Jia, S. & Fleischer, J. W. Nonlinear light propagation in fractal waveguide arrays. Opt. Express 18, 14409–14415 (2010).
Osellame, R., Cerullo, G. & Ramponi, R. (eds) Femtosecond Laser Micromachining: Photonic and Microfluidic Devices in Transparent Materials Vol. 123 (Springer, 2012).
Xu, X.-Y. et al. A scalable photonic computer solving the subset sum problem. Sci. Adv. 6, eaay5853 (2020).
Darázs, Z. & Kiss, T. Pólya number of the continuous-time quantum walks. Phys. Rev. A 81, 062319 (2010).
Fleischmann, R., Geisel, T., Ketzmerick, R. & Petschel, G. Quantum diffusion, fractal spectra, and chaos in semiconductor microstructures. Physica D 86, 171–181 (1995).
Hameroff, S. & Penrose, R. Consciousness in the universe: a review of the ‘Orch OR’ theory. Phys. Life Rev. 11, 39–78 (2014).
Hameroff, S. & Penrose, R. Orchestrated reduction of quantum coherence in brain microtubules: a model for consciousness. Math. Comput. Simul. 40, 453–480 (1996).
Gefen, Y., Aharony, A., Mandelbrot, B. B. & Kirkpatrick, S. Solvable fractal family, and its possible relation to the backbone at percolation. Phys. Rev. Lett. 47, 1771 (1981).
Agliari, E., Blumen, A. & Mülken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 82, 012305 (2010).
Acknowledgements
We thank J.-W. Pan for helpful discussions, X.-L. Huang and Z.-M. Li for helping in the experiments, J. Gao, R.-J. Ren and S. Freeney for proof reading, and W.-H. Zhou for assistance in formatting the figures. This research is supported by the National Key R&D Program of China (2019YFA0308700, 2019YFA0706302 and 2017YFA0303700); National Natural Science Foundation of China (NSFC) (11904229, 61734005, 11761141014, 11690033); Science and Technology Commission of Shanghai Municipality (STCSM) (20JC1416300, 2019SHZDZX01); Shanghai Municipal Education Commission (SMEC) (2017-01-07-00-02-E00049); China Postdoctoral Science Foundation (2021M692094, 2020M671091). X.-M.J. acknowledges additional support from a Shanghai talent program and support from Zhiyuan Innovative Research Center of Shanghai Jiao Tong University.
Author information
Authors and Affiliations
Contributions
X.-M.J. conceived and supervised the project. X.-Y.X. performed the simulations and fabricated the photonic chips. X.-Y.X., X.-W.W., D.-Y.C. and X.-M.J. performed the experiments and analysed the data. X.-Y.X., C.M.S. and X.-M.J. interpreted the data and wrote the paper, with input from all the other authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Photonics thanks Eric Heller and Shengjun Yuan for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplemental Information
Supplementary Figs. 1–27 and Discussion.
Supplementary Video 1
The dynamical evolution of the MSD for the Sierpiński gasket and the corresponding evolution patterns of photons.
Supplementary Video 2
The dynamical evolution of the MSD for the Sierpiński carpet and the corresponding evolution patterns of photons.
Supplementary Video 3
The dynamical evolution of the MSD for the dual Sierpiński carpet and the corresponding evolution patterns of photons.
Rights and permissions
About this article
Cite this article
Xu, XY., Wang, XW., Chen, DY. et al. Quantum transport in fractal networks. Nat. Photon. 15, 703–710 (2021). https://doi.org/10.1038/s41566-021-00845-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-021-00845-4
This article is cited by
-
Fractal photonic anomalous Floquet topological insulators to generate multiple quantum chiral edge states
Light: Science & Applications (2023)
-
Photonic elementary cellular automata for simulation of complex phenomena
Light: Science & Applications (2023)
-
Photons walk on fractal graphs
Nature Photonics (2021)