Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

A high-fidelity heralded quantum squeezing gate

Nature Photonics volume 14, pages 306–309 (2020)Cite this article

Subjects

Abstract

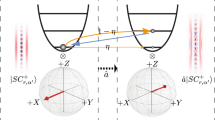
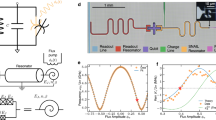
Squeezing operation is critical for continuous-variable quantum information, enabling encoding of information in phase space to a resolution otherwise forbidden by vacuum noise1. A universal squeezing gate that can squeeze arbitrary input states is particularly essential for continuous-variable quantum computation2,3. However, the fidelity of existing state-of-the-art implementations is ultimately limited due to their reliance on first synthesizing squeezed vacuum modes of unbounded energy4,5. Here, we circumvent this fundamental limitation by using a heralded squeezing gate. This allows improved gate fidelity without requiring more squeezed ancillary vacuum. For a specific target squeezing level for coherent states, we present measured fidelities higher than what would be possible using non-heralded schemes that utilize up to 15 dB (ref. 6) of best available ancilla squeezing. Our technique can be applied to non-Gaussian states and provides a promising pathway towards high-fidelity gate operations and fault-tolerant continuous-variable quantum computation.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental layout of the heralded squeezing gate.
Fig. 2: Fidelity against success probability for various target squeezing values.
Fig. 3: Phase-space diagram for the squeezing gate.
Fig. 4: Improvement in fidelity over conventional techniques for a series of target squeezing values for states A–E.
Fig. 5: Fidelity as a function of filter strength and ancillary squeezing.

Similar content being viewed by others

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

References

  1. Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012).

    Article  ADS  Google Scholar 

  2. Mile, G., Weedbrook, C., Menicucci, N. C., Ralph, T. C. & van Loock, P. Quantum computing with continuous-variable clusters. Phys. Rev. A 79, 062318 (2009).

    Article  ADS  Google Scholar 

  3. Menicucci, N. C. Fault-tolerant measurement-based quantum computing with continuous-variable cluster states. Phys. Rev. Lett. 112, 120504 (2014).

    Article  ADS  Google Scholar 

  4. Miyata, K. et al. Experimental realization of a dynamic squeezing gate. Phys. Rev. A 90, 060302 (2014).

    Article  ADS  Google Scholar 

  5. Ukai, R. et al. Demonstration of unconditional one-way quantum computations for continuous variables. Phys. Rev. Lett. 106, 240504 (2011).

    Article  ADS  Google Scholar 

  6. Vahlbruch, H., Mehmet, M., Danzmann, K. & Schnabel, R. Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. Phys. Rev. Lett. 117, 110801 (2016).

    Article  ADS  Google Scholar 

  7. Menicucci, N. C., Ma, X. & Ralph, T. C. Arbitrarily large continuous-variable cluster states from a single quantum nondemolition gate. Phys. Rev. Lett. 104, 250503 (2010).

    Article  ADS  Google Scholar 

  8. Braustein, S. L. Squeezing as an irreducible resource. Phys. Rev. A 71, 055801 (2005).

    Article  ADS  Google Scholar 

  9. Yurke, B. Optical back-action-evading amplifiers. J. Opt. Soc. Am. B 2, 732–738 (1985).

    Article  ADS  Google Scholar 

  10. Yoshikawa, J.-I. et al. Demonstration of a quantum nondemolition sum gate. Phys. Rev. Lett. 101, 250501 (2008).

    Article  MathSciNet  ADS  Google Scholar 

  11. Puri, S. & Blais, A. High-fidelity resonator-induced phase gate with single-mode squeezing. Phys. Rev. Lett. 116, 180501 (2016).

    Article  ADS  Google Scholar 

  12. Braustein, S. L. Error correction for continuous quantum variables. Phys. Rev. Lett. 80, 4084–4087 (1998).

    Article  ADS  Google Scholar 

  13. LeJeannic, H., Cavailles, A., Huang, K., Filip, R. & Laurat, J. Slowing quantum decoherence by squeezing in phase space. Phys. Rev. Lett. 120, 073603 (2018).

    Article  ADS  Google Scholar 

  14. Miwa, Y. et al. Exploring a new regime for processing optical qubits: squeezing and unsqueezing single photons. Phys. Rev. Lett. 113, 013601 (2014).

    Article  ADS  Google Scholar 

  15. Takeoka, M. & Sasaki, M. Discrimination of the binary coherent signal: Gaussian-operation limit and simple non-Gaussian near-optimal receivers. Phys. Rev. A 78, 022320 (2008).

    Article  ADS  Google Scholar 

  16. Andersen, U. L., Gehring, T., Marquardt, C. & Leuchs, G. 30 years of squeezed light generation. Phys. Scr. 91, 053001 (2016).

    Article  ADS  Google Scholar 

  17. Yoshikawa, J.-I. et al. Demonstration of deterministic and high fidelity squeezing of quantum information. Phys. Rev. A 76, 060301 (2007).

    Article  ADS  Google Scholar 

  18. Su, X. et al. Gate sequence for continuous variable one-way quantum computation. Nat. Commun. 4, 2828 (2013).

    Article  ADS  Google Scholar 

  19. de Oliveira, F. A. M. & Knight, P. L. Bright squeezing. Phys. Rev. Lett. 61, 830–833 (1988).

    Article  ADS  Google Scholar 

  20. LaPorta, A., Slusher, R. E. & Yurke, B. Back-action evading measurements of an optical field using parametric down conversion. Phys. Rev. Lett. 62, 28–31 (1989).

    Article  ADS  Google Scholar 

  21. Zhang, J., Ye, C., Gao, F. & Xiao, M. Phase-sensitive manipulations of a squeezed vacuum field in an optical parametric amplifier inside an optical cavity. Phys. Rev. Lett. 101, 233602 (2008).

    Article  ADS  Google Scholar 

  22. Ma, H., Ye, C., Wei, D. & Zhang, J. Coherence phenomena in the phase-sensitive optical parametric amplification inside a cavity. Phys. Rev. Lett. 95, 233601 (2005).

    Article  ADS  Google Scholar 

  23. Fiurášek, J. & Cerf, N. J. Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution. Phys. Rev. A 86, 060302 (2012).

    Article  ADS  Google Scholar 

  24. Chrzanowski, H. M. et al. Measurement-based noiseless linear amplification for quantum communication. Nat. Photon. 8, 333–338 (2014).

    Article  ADS  Google Scholar 

  25. Zhao, J., Hao, J. Y., Symul, T., Lam, P. K. & Assad, S. M. Characterization of a measurement-based noiseless linear amplifier and its applications. Phys. Rev. A 96, 012319 (2017).

    Article  ADS  Google Scholar 

  26. Laurat, J., Coudreau, T., Treps, N., Matre, A. & Fabre, C. Conditional preparation of a quantum state in the continuous variable regime: generation of a sub-Poissonian state from twin beams. Phys. Rev. Lett. 91, 213601 (2003).

    Article  ADS  Google Scholar 

  27. Andersen, U. L., Neergaard-Nielsen, J. S., van Loock, P. & Furusawa, A. Hybrid discrete- and continuous-variable quantum information. Nat. Phys. 11, 713–719 (2015).

    Article  Google Scholar 

  28. van Loock, P. Optical hybrid approaches to quantum information. Laser Photon. Rev. 5, 167–200 (2011).

    Article  ADS  Google Scholar 

  29. Ralph, T. C. Coherent superposition states as quantum rulers. Phys. Rev. A 65, 042313 (2002).

    Article  ADS  Google Scholar 

  30. Munro, W. J., Nemoto, K., Milburn, G. J. & Braustein, S. L. Weak-force detection with superposed coherent states. Phys. Rev. A 66, 023819 (2002).

    Article  ADS  Google Scholar 

  31. Menicucci, N. C. et al. Universal quantum computation with continuous-variable cluster states. Phys. Rev. Lett. 97, 110501 (2006).

    Article  ADS  Google Scholar 

  32. Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat. Photon. 7, 229–233 (2013).

    Article  ADS  Google Scholar 

  33. Bash, B. A., Gagatsos, C. N., Datta, A. & Guha, S. Fundamental limits of quantum-secure covert optical sensing. In Proc. 2017 IEEE Int. Symp. on Information Theory 3210–3214 (IEEE, 2017).

Download references

Acknowledgements

The research is supported by the Australian Research Council (ARC) under the Centre of Excellence for Quantum Computation and Communication Technology (CE110001027). K.L. is supported by the National Natural Science Foundation of China (grants 11674205 and 91536222). M.G. acknowledges funding from The National Research Foundation of Singapore (NRF Fellowship reference no. NRF-NRFF2016-02) and the Singapore Ministry of Education Tier 1 RG190/17. M.G. thanks the Institute of Advanced Study at NTU for funding the travel that catalysed this work. P.K.L. is an ARC Laureate Fellow.

Author information

Author notes

  1. These authors contributed equally: Jie Zhao, Kui Liu.

Authors and Affiliations

  1. Centre of Excellence for Quantum Computation and Communication Technology, Department of Quantum Science, Research School of Physics and Engineering, The Australian National University, Canberra, Australian Capital Territory, Australia

    Jie Zhao, Hao Jeng, Ping Koy Lam & Syed M. Assad

  2. State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, China

    Kui Liu

  3. School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, Singapore

    Mile Gu

  4. Complexity Institute, Nanyang Technological University, Singapore, Singapore

    Mile Gu

  5. Centre for Quantum Technologies, National University of Singapore, Singapore, Singapore

    Mile Gu & Jayne Thompson

Authors
  1. Jie Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hao Jeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mile Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jayne Thompson
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ping Koy Lam
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Syed M. Assad
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.M.A., J.Z., M.G., J.T. and P.K.L. conceived the experiment. S.M.A. and J.Z. developed the theoretical model. J.Z., K.L., H.J., S.M.A. and P.K.L. planned and performed the experiment. J.Z. and S.M.A. analysed the data. J.Z., S.M.A., H.J., J.T., M.G. and P.K.L. drafted the initial manuscript. All authors discussed the results and commented on the manuscript.

Corresponding author

Correspondence to Ping Koy Lam.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

The Supplementary Information includes seven sections, Supplementary Figs. 1–7 and Supplementary Table 1.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, J., Liu, K., Jeng, H. et al. A high-fidelity heralded quantum squeezing gate. Nat. Photonics 14, 306–309 (2020). https://doi.org/10.1038/s41566-020-0592-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41566-020-0592-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing