Abstract
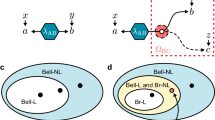
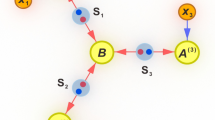
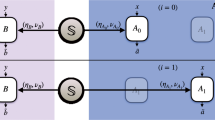
The ongoing interest in creating a secure global quantum network culminated recently in the demonstration of transcontinental quantum communication1. There is a pressing need to examine the properties attached to a quantum network architecture from multiple perspectives, including physics foundations2, communication security3, the efficient use of resources and innovative technological applications4,5. Here, we present an experimental realization of a five-node quantum network, in which quantum sources at two nodes deliver entangled photon pairs to three measurement nodes. With relevant events between five nodes separated space-like, we demonstrate violation of the Bell inequality and bilocal inequality6, with the locality, measurement independence and quantum source independence loopholes closed simultaneously in a quantum network. This experimental realization may be valuable for the design and implementation of future quantum networks.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Vazirani, U. & Vidick, T. Fully device-independent quantum key distribution. Phys. Rev. Lett. 113, 140501 (2014).
Colbeck, R. A. Quantum and Relativistic Protocols for Secure Multi-party Computation. PhD thesis, Univ. Cambridge (2007).
Lee, C. M. & Hoban, M. J. Towards device-independent information processing on general quantum networks. Phys. Rev. Lett. 120, 020504 (2018).
Branciard, C., Gisin, N. & Pironio, S. Characterizing the nonlocal correlations created via entanglement swapping. Phys. Rev. Lett. 104, 170401 (2010).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Bell, J. S. On the Einstein–Podolsky–Rosen paradox. Physics 1, 195–200 (1964).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).
Chaves, R., Kueng, R., Brask, J. B. & Gross, D. Unifying framework for relaxations of the causal assumptions in Bell’s theorem. Phys. Rev. Lett. 114, 140403 (2015).
Chaves, R. Polynomial Bell inequalities. Phys. Rev. Lett. 116, 010402 (2016).
Rosset, D. et al. Nonlinear Bell inequalities tailored for quantum networks. Phys. Rev. Lett. 116, 010403 (2016).
Fritz, T. Beyond Bell’s theorem II: scenarios with arbitrary causal structure. Commun. Math. Phys. 341, 391–434 (2016).
Żukowski, M., Zeilinger, A., Horne, M. & Ekert, A. ‘Event-ready-detectors’ Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Aspect, A., Grangier, P. & Roger, G. Experimental tests of realistic local theories via Bell’s theorem. Phys. Rev. Lett. 47, 460–463 (1981).
Carvacho, G. et al. Experimental violation of local causality in a quantum network. Nat. Commun. 8, 14775 (2017).
Saunders, D. J., Bennet, A. J., Branciard, C. & Pryde, G. J. Experimental demonstration of nonbilocal quantum correlations. Sci. Adv. 3, e1602743 (2017).
Andreoli, F. et al. Experimental bilocality violation without shared reference frames. Phys. Rev. A 95, 062315 (2017).
Weinfurter, H. Experimental Bell-state analysis. Europhys. Lett. 25, 559–564 (1994).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Sun, Q.-C. et al. Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Photon. 10, 671–675 (2016).
Abellán, C., Amaya, W., Mitrani, D., Pruneri, V. & Mitchell, M. W. Generation of fresh and pure random numbers for loophole-free Bell tests. Phys. Rev. Lett. 115, 250403 (2015).
Hong, C., Ou, Z. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Handsteiner, J. et al. Cosmic Bell test: measurement settings from Milky Way stars. Phys. Rev. Lett. 118, 060401 (2017).
Li, M.-H. et al. Test of local realism into the past without detection and locality loopholes. Phys. Rev. Lett. 121, 080404 (2018).
Tavakoli, A., Skrzypczyk, P., Cavalcanti, D. & Acín, A. Nonlocal correlations in the star-network configuration. Phys. Rev. A 90, 062109 (2014).
Andreoli, F., Carvacho, G., Santodonato, L., Chaves, R. & Sciarrino, F. Maximal qubit violation of n-locality inequalities in a star-shaped quantum network. New J. Phys. 19, 113020 (2017).
Gisin, N. The elegant joint quantum measurement and some conjectures about n-locality in the triangle and other configurations. Preprint at http://arxiv.org/abs/1708.05556 (2017).
Branciard, C., Rosset, D., Gisin, N. & Pironio, S. Bilocal versus nonbilocal correlations in entanglement-swapping experiments. Phys. Rev. A 85, 032119 (2012).
Acknowledgements
We thank Y. Liu, Y. Li and Y.-Q. Nie for enlightening discussions, Y.-L. Mao for assistance, K.-X. Yang for help with the aerial photographs and Quantum Ctek for providing the components used in the QRNGs. This work was supported by the National Key R&D Program of China (2017YFA0303900, 2017YFA0304000), the National Natural Science Foundation of China and the Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
Q.-C.S., Q.Z., J.F. and J.-W.P. conceived and designed the experiments. B.B. and J.Z. built the QRNGs. W.Z., H.L., L.Y. and Z.W. fabricated the SNSPDs. Q.-C.S. and Y.-F.J. built the experimental network and carried out the experiment. X.J. and X.C. provided experimental assistance. Q.-C.S. and Y.-F.J. analysed the data. Q.-C.S., Q.Z., J.F. and J.-W.P. wrote the manuscript, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Sun, QC., Jiang, YF., Bai, B. et al. Experimental demonstration of non-bilocality with truly independent sources and strict locality constraints. Nat. Photonics 13, 687–691 (2019). https://doi.org/10.1038/s41566-019-0502-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0502-7
This article is cited by
-
Experimental nonclassicality in a causal network without assuming freedom of choice
Nature Communications (2023)
-
Certification of non-classicality in all links of a photonic star network without assuming quantum mechanics
Nature Communications (2023)
-
Demonstrating the power of quantum computers, certification of highly entangled measurements and scalable quantum nonlocality
npj Quantum Information (2021)
-
Quantum theory based on real numbers can be experimentally falsified
Nature (2021)
-
Experimental violation of n-locality in a star quantum network
Nature Communications (2020)