Abstract
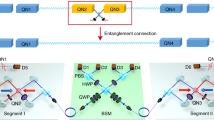
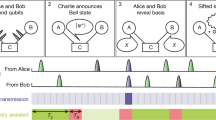
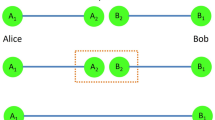
Quantum repeaters—important components of a scalable quantum internet—enable entanglement to be distributed over long distances. The standard paradigm for a quantum repeater relies on the necessary, demanding requirement of quantum memory. Despite significant progress, the limited performance of quantum memory means that making practical quantum repeaters remains a challenge. Remarkably, a proposed all-photonic quantum repeater avoids the need for quantum memory by harnessing the graph states in the repeater nodes. Here we perform an experimental demonstration of an all-photonic quantum repeater. By manipulating a 12-photon interferometer, we implement a 2 × 2 parallel all-photonic quantum repeater, and observe an 89% enhancement of entanglement-generation rate over standard parallel entanglement swapping. These results provide a new approach to designing repeaters with efficient single-photon sources and photonic graph states, and suggest that the all-photonic scheme represents an alternative path—parallel to matter-memory-based schemes—towards realizing practical quantum repeaters.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photon. 8, 595–604 (2014).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Yin, J. et al. Satellite-based entanglement distribution over 1,200 kilometers. Science 356, 1140–1144 (2017).
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L.-M., Lukin, M., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Żukowski, M., Zeilinger, A., Horne, M. A. & Ekert, A. K. ‘Event-ready-detectors’ Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Pan, J.-W., Bouwmeester, D., Weinfurter, H. & Zeilinger, A. Experimental entanglement swapping: entangling photons that never interacted. Phys. Rev. Lett. 80, 3891–3894 (1998).
Pan, J.-W., Simon, C., Brukner, Č. & Zeilinger, A. Entanglement purification for quantum communication. Nature 410, 1067–1070 (2001).
Pan, J.-W., Gasparoni, S., Ursin, R., Weihs, G. & Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 423, 417–422 (2003).
Chou, C.-W. et al. Functional quantum nodes for entanglement distribution over scalable quantum networks. Science 316, 1316–1320 (2007).
Moehring, D. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Yuan, Z.-S. et al. Experimental demonstration of a BDCZ quantum repeater node. Nature 454, 1098–1101 (2008).
Zwerger, M., Dür, W. & Briegel, H. J. Measurement-based quantum repeaters. Phys. Rev. A 85, 062326 (2012).
Munro, W., Stephens, A., Devitt, S., Harrison, K. & Nemoto, K. Quantum communication without the necessity of quantum memories. Nat. Photon. 6, 777–781 (2012).
Muralidharan, S., Kim, J., Lütkenhaus, N., Lukin, M. D. & Jiang, L. Ultrafast and fault-tolerant quantum communication across long distances. Phys. Rev. Lett. 112, 250501 (2014).
Chen, L.-K. et al. Experimental nested purification for a linear optical quantum repeater. Nat. Photon. 11, 695–699 (2017).
Xu, P. et al. Two-hierarchy entanglement swapping for a linear optical quantum repeater. Phys. Rev. Lett. 119, 170502 (2017).
Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
Yang, S.-J., Wang, X.-J., Bao, X.-H. & Pan, J.-W. An efficient quantum light–matter interface with sub-second lifetime. Nat. Photon. 10, 381–384 (2016).
Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 6, 6787 (2015).
Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001).
Bruschi, D. E., Barlow, T. M., Razavi, M. & Beige, A. Repeat-until-success quantum repeaters. Phys. Rev. A 90, 032306 (2014).
Pant, M., Krovi, H., Englund, D. & Guha, S. Rate-distance tradeoff and resource costs for all-optical quantum repeaters. Phys. Rev. A 95, 012304 (2017).
Buterakos, D., Barnes, E. & Economou, S. E. Deterministic generation of all-photonic quantum repeaters from solid-state emitters. Phys. Rev. X 7, 041023 (2017).
Ewert, F., Bergmann, M. & van Loock, P. Ultrafast long-distance quantum communication with static linear optics. Phys. Rev. Lett. 117, 210501 (2016).
Ewert, F. & van Loock, P. Ultrafast fault-tolerant long-distance quantum communication with static linear optics. Phys. Rev. A 95, 012327 (2017).
Hasegawa, Y. et al. Experimental time-reversed adaptive Bell measurement towards all-photonic quantum repeaters. Nat. Commun. 10, 378 (2019).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Luis, A. & Sánchez-Soto, L. L. Complete characterization of arbitrary quantum measurement processes. Phys. Rev. Lett. 83, 3573–3576 (1999).
Acknowledgements
The authors thank H.-K. Lo for helpful discussions. This work was supported by the National Key Research and Development (R&D) Plan of China (grants 2018YFB0504300 and 2018YFA0306501), the National Natural Science Foundation of China (grants 11425417, 61771443 and U1738140), the Anhui Initiative in Quantum Information Technologies and the Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
Z.-D.L., F.X., Y.-A.C. and J.-W.P. conceived and designed the experiments. Z.-D.L., F.X. and Y.-A.C. designed and characterized the multiphoton optical circuits. Z.-D.L., R.Z., X.-F.Y., L.-Z.L., Y.H., Y.-Q.F. and Y.-Y.F. carried out the experiments. Z.-D.L., R.Z., F.X. and Y.-A.C. analysed the data. All authors discussed the results and wrote the manuscript. F.X., Y.-A.C. and J.-W.P. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures
Rights and permissions
About this article
Cite this article
Li, ZD., Zhang, R., Yin, XF. et al. Experimental quantum repeater without quantum memory. Nat. Photonics 13, 644–648 (2019). https://doi.org/10.1038/s41566-019-0468-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0468-5
This article is cited by
-
Towards metropolitan free-space quantum networks
npj Quantum Information (2023)
-
Surpassing the repeaterless bound with a photon-number encoded measurement-device-independent quantum key distribution protocol
npj Quantum Information (2023)
-
A photonic entanglement filter with Rydberg atoms
Nature Photonics (2023)
-
Optimal quantum network decongestion strategies
Scientific Reports (2023)
-
Applications of single photons to quantum communication and computing
Nature Reviews Physics (2023)