Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Knotting fractional-order knots with the polarization state of light

Nature Photonics volume 13, pages 569–574 (2019)Cite this article

Subjects

This article has been updated

Abstract

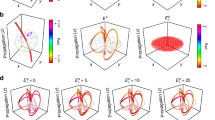
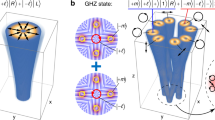
The fundamental polarization singularities of monochromatic light are normally associated with invariance under coordinated rotations: symmetry operations that rotate the spatial dependence of an electromagnetic field by an angle θ and its polarization by a multiple γθ of that angle. These symmetries are generated by mixed angular momenta of the form Jγ = L + γS, and they generally induce Möbius-strip topologies, with the coordination parameter γ restricted to integer and half-integer values. In this work we construct beams of light that are invariant under coordinated rotations for arbitrary rational γ, by exploiting the higher internal symmetry of ‘bicircular’ superpositions of counter-rotating circularly polarized beams at different frequencies. We show that these beams have the topology of a torus knot, which reflects the subgroup generated by the torus-knot angular momentum Jγ, and we characterize the resulting optical polarization singularity using third- and higher-order field moment tensors, which we experimentally observe using nonlinear polarization tomography.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Coordinated-rotation invariance and torus-knot beam topology.
Fig. 2: Possible topologies of torus-knot beams.
Fig. 3: Experimental configuration and results.

Similar content being viewed by others

Data availability

The data used to generate the experimental figures in this paper have been publicly archived in the Zenodo repository at https://doi.org/10.5281/zenodo.2649391.

Code availability

The code used to generate the theoretical figures, and the scripts used to process the experimental data, have been publicly archived in the Zenodo repository at https://doi.org/10.5281/zenodo.2649391.

Change history

  • 21 August 2019

    When this Article was originally published, the file for Supplementary Data 1 was missing; it has now been added.

References

  1. Torres, J. P. & Torner, L. (eds) Twisted Photons: Applications of Light with Orbital Angular Momentum (Wiley, 2011).

  2. Andrews, D. L. & Babiker, M. (eds) The Angular Momentum of Light (Cambridge University Press, 2012).

  3. Gbur, G. Singular Optics (CRC Press, 2016).

  4. Rubinsztein-Dunlop, H. et al. Roadmap on structured light. J. Opt. 19, 013001 (2017).

    Article  ADS  Google Scholar 

  5. Nye, J. F. & Berry, M. V. Dislocations in wave trains. Proc. R. Soc. A 336, 165–190 (1974).

    Article  ADS  MathSciNet  Google Scholar 

  6. Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 6, 488–491 (2012).

    Article  ADS  Google Scholar 

  7. Fürhapter, S., Jesacher, A., Bernet, S. & Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 13, 689–694 (2005).

    Article  ADS  Google Scholar 

  8. Garcés-Chávez, V., Volke-Sepulveda, K., Chávez-Cerda, S., Sibbett, W. & Dholakia, K. Transfer of orbital angular momentum to an optically trapped low-index particle. Phys. Rev. A 66, 063402 (2002).

    Article  ADS  Google Scholar 

  9. Padgett, M. & Bowman, R. Tweezers with a twist. Nat. Photon 5, 343–348 (2011).

    Article  ADS  Google Scholar 

  10. Hernández-García, C. et al. Generation and applications of extreme-ultraviolet vortices. Photonics 4, 28 (2017).

    Article  Google Scholar 

  11. Barnett, S. M. et al. On the natures of the spin and orbital parts of optical angular momentum. J. Opt. 18, 064004 (2016).

    Article  ADS  Google Scholar 

  12. Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. Nat. Phys. 3, 305–310 (2007).

    Article  Google Scholar 

  13. Van Enk, S. & Nienhuis, G. Spin and orbital angular momentum of photons. Eur. Phys. Lett. 25, 497–501 (1994).

    Article  ADS  Google Scholar 

  14. Kedia, H., Bialynicki-Birula, I., Peralta-Salas, D. & Irvine, W. T. M. Tying knots in light fields. Phys. Rev. Lett. 111, 150404 (2013).

    Article  ADS  Google Scholar 

  15. Leach, J., Dennis, M. R., Courtial, J. & Padgett, M. J. Laser beams: knotted threads of darkness. Nature 432, 165 (2004).

    Article  ADS  Google Scholar 

  16. Dennis, M. R., King, R. P., Jack, B., O’Holleran, K. & Padgett, M. J. Isolated optical vortex knots. Nat. Phys. 6, 118–121 (2010).

    Article  Google Scholar 

  17. Sugic, D. & Dennis, M. R. Knotted hopfion in tightly focused light. In Proceedings of the 4th International Conference on Optical Angular Momentum (ed. Marrucci, L.) 137 (Jean Gilder, 2017); http://www.jeangilder.it/icoam2017/abstract-book/

  18. Larocque, H. et al. Reconstructing the topology of optical polarization knots. Nat. Phys. 14, 1079–1082 (2018).

    Article  Google Scholar 

  19. Freund, I. Cones, spirals and Möbius strips, in elliptically polarized light. Opt. Commun. 249, 7–22 (2005).

    Article  ADS  Google Scholar 

  20. Nye, J. F. & Hajnal, J. V. The wave structure of monochromatic electromagnetic radiation. Proc. R. Soc. Lond. A 409, 21–36 (1987).

    Article  ADS  MathSciNet  Google Scholar 

  21. Dennis, M. R. Polarization singularities in paraxial vector fields: morphology and statistics. Opt. Commun. 213, 201–221 (2002).

    Article  ADS  Google Scholar 

  22. Bauer, T. et al. Multi-twist polarization ribbon topologies in highly-confined optical fields. Preprint at http://arxiv.org/abs/1901.11337 (2019).

  23. Freund, I. Optical Möbius strips in three-dimensional ellipse fields: I. Lines of circular polarization. Opt. Commun. 283, 1–15 (2010).

    Article  ADS  Google Scholar 

  24. Freund, I. Optical Möbius strips in three-dimensional ellipse fields: II. Lines of circular polarization. Opt. Commun. 283, 16–28 (2010).

    Article  ADS  Google Scholar 

  25. Bauer, T. et al. Observation of optical polarization Möbius strips. Science 347, 964–966 (2015).

    Article  ADS  Google Scholar 

  26. Bauer, T., Neugebauer, M., Leuchs, G. & Banzer, P. Optical polarization Möbius strips and points of purely transverse spin density. Phys. Rev. Lett. 117, 013601 (2016).

    Article  ADS  Google Scholar 

  27. Galvez, E. J. et al. Multitwist Möbius strips and twisted ribbons in the polarization of paraxial light beams. Sci. Rep. 7, 13653 (2017).

    Article  ADS  Google Scholar 

  28. Garcia-Etxarri, A. Optical polarization Möbius strips on all-dielectric optical scatterers. ACS Photonics 4, 1159–1164 (2017).

    Article  Google Scholar 

  29. Cardano, F. & Marrucci, L. Spin–orbit photonics. Nat. Photon 9, 776–778 (2015).

    Article  ADS  Google Scholar 

  30. Bliokh, K. Y., Rodríguez-Fortuño, F. J., Nori, F. & Zayats, A. V. Spin–orbit interactions of light. Nat. Photon. 9, 796–808 (2015).

    Article  ADS  Google Scholar 

  31. Bliokh, K. Y. Geometrodynamics of polarized light: Berry phase and spin Hall effect in a gradient-index medium. J. Opt. A Pure Appl. Opt. 11, 094009 (2009).

    Article  ADS  Google Scholar 

  32. Ballantine, K. E., Donegan, J. F. & Eastham, P. R. There are many ways to spin a photon: half-quantization of a total optical angular momentum. Sci. Adv. 2, e1501748 (2016).

    Article  ADS  Google Scholar 

  33. Leach, J. et al. Interferometric methods to measure orbital and spin, or the total angular momentum of a single photon. Phys. Rev. Lett. 92, 013601 (2004).

    Article  ADS  Google Scholar 

  34. Galvez, E. J., Coyle, L. E., Johnson, E. & Reschovsky, B. J. Interferometric measurement of the helical mode of a single photon. New J. Phys. 13, 053017 (2011).

    Article  ADS  Google Scholar 

  35. Kessler, D. A. & Freund, I. Lissajous singularities. Opt. Lett. 28, 111–113 (2003).

    Article  ADS  Google Scholar 

  36. Freund, I. Bichromatic optical Lissajous fields. Opt. Commun. 226, 351–376 (2003).

    Article  ADS  Google Scholar 

  37. Fleischer, A., Kfir, O., Diskin, T., Sidorenko, P. & Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photon. 8, 543–549 (2014).

    Article  ADS  Google Scholar 

  38. Freund, I. Polychromatic polarization singularities. Opt. Lett. 28, 2150–2152 (2003).

    Article  ADS  Google Scholar 

  39. Freund, I. Polarization critical points in polychromatic optical fields. Opt. Commun. 227, 61–71 (2003).

    Article  ADS  Google Scholar 

  40. Yan, H. & Lü, B. Dynamical evolution of Lissajous singularities in free-space propagation. Phys. Lett. A 374, 3695–3700 (2010).

    Article  ADS  Google Scholar 

  41. Haitao, C., Gao, Z. & Wang, W. Propagation of the Lissajous singularity dipole emergent from non-paraxial polychromatic beams. Opt. Commun. 393, 17–24 (2017).

    Article  ADS  Google Scholar 

  42. Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots (American Mathematical Society, 2004).

  43. Rolfsen, D. Knots and Links 17–18 (American Mathematical Society, 2003).

  44. Götte, J. B. et al. Light beams with fractional orbital angular momentum and their vortex structure. Opt. Express 16, 993–1006 (2008).

    Article  ADS  Google Scholar 

  45. Freund, I. Coherency matrix description of optical polarization singularities. J. Opt. A Pure Appl. Opt. 6, S229 (2004).

    Article  ADS  Google Scholar 

  46. Samim, M., Krouglov, S. & Barzda, V. Nonlinear Stokes–Mueller polarimetry. Phys. Rev. A 93, 013847 (2016).

    Article  ADS  Google Scholar 

  47. Maucher, F., Skupin, S., Gardiner, S. A. & Hughes, I. G. Creating complex optical longitudinal polarization structures. Phys. Rev. Lett. 120, 163903 (2018).

    Article  ADS  Google Scholar 

  48. Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 49, 957–959 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  49. Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).

    Article  ADS  Google Scholar 

  50. Lin, Y.-J., Jiménez-García, K. & Spielman, I. B. Spin–orbit-coupled Bose–Einstein condensates. Nature 471, 83–86 (2011).

    Article  ADS  Google Scholar 

  51. Maucher, F., Gardiner, S. A. & Hughes, I. G. Excitation of knotted vortex lines in matter waves. New J. Phys. 18, 063016 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  52. Bloembergen, N. Conservation laws in nonlinear optics. J. Opt. Soc. Am. 70, 1429–1436 (1980).

    Article  ADS  Google Scholar 

  53. Hickstein, D. D. et al. Non-collinear generation of angularly isolated circularly polarized high harmonics. Nat. Photon. 9, 743–750 (2015).

    Article  ADS  Google Scholar 

  54. Pisanty, E. et al. Conservation of torus-knot angular momentum in high-order harmonic generation. Phys. Rev. Lett. 122, 203201 (2019).

    Article  ADS  Google Scholar 

  55. Pisanty, E. LISSAFIRE: Lissajous-figure reconstruction for nonlinear polarization tomography of bichromatic fields https://github.com/episanty/LISSAFIRE (GitHub); v1.0.2 https://doi.org/10.5281/zenodo.2649390 (Zenodo, 2019).

  56. Pisanty, E. et al. Code and data for ‘Knotting fractional-order knots with the polarization state of light’ https://doi.org/10.5281/zenodo.2649391 (Zenodo, 2019).

Download references

Acknowledgements

The authors thank M. Maffei and I. Freund for helpful conversations, and X. Menino for 3D-printing assistance. E.P. acknowledges Cellex-ICFO-MPQ fellowship funding. E.P., M.L. and A.C. acknowledge funding from the Spanish Ministry MINECO (National Plan 15 Grant: FISICATEAMO no. FIS2016-79508-P, SEVERO OCHOA no. SEV-2015-0522, FPI), the European Social Fund, Fundació Cellex, Generalitat de Catalunya (AGAUR grant no. 2017 SGR 1341 and CERCA/Program), ERC AdG OSYRIS, EU FETPRO QUIC and the National Science Centre, Poland-Symfonia grant no. 2016/20/W/ST4/00314. V.V.-H. acknowledges financial support from Secretaría de Ciencia, Tecnología e Innovación de la Ciudad de México. J.P.T. acknowledges support from Generalitat de Catalunya (Program ICREA Academia). G.J.M. was supported by the Secretaria d’Universitats i Recerca del Departament d’Economia i Coneixement de la Generalitat de Catalunya, as well as the European Social Fund—FEDER. A.P. acknowledges funding from Comunidad de Madrid through TALENTO grant ref. 2017-T1/IND-5432. A.C. acknowledges financial support from the ERC Synergy Grant UQUAM, the SFB FoQuS (FWF project no. F4016-N23), the UAB Talent Research programme and from the Spanish Ministry of Economy and Competitiveness under contract no. FIS2017-86530-P.

Author information

Authors and Affiliations

  1. ICFO - Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, Av. Carl Friedrich Gauss 3, 08860, Castelldefels (Barcelona), Spain

    Emilio Pisanty, Gerard J. Machado, Verónica Vicuña-Hernández, Antonio Picón, Alessio Celi, Juan P. Torres & Maciej Lewenstein

  2. Departamento de Química, Universidad Autónoma de Madrid, Madrid, Spain

    Antonio Picón

  3. Center for Quantum Physics, University of Innsbruck, Innsbruck, Austria

    Alessio Celi

  4. Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences, Innsbruck, Austria

    Alessio Celi

  5. Departament de Física, Universitat Autònoma de Barcelona, Bellaterra, Spain

    Alessio Celi

  6. Department of Signal Theory and Communications, Universitat Politecnica de Catalunya, Barcelona, Spain

    Juan P. Torres

  7. ICREA, Pg. Lluís Companys 23, 08010, Barcelona, Spain

    Maciej Lewenstein

Authors
  1. Emilio Pisanty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gerard J. Machado
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Verónica Vicuña-Hernández
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Antonio Picón
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Alessio Celi
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Juan P. Torres
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Maciej Lewenstein
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

E.P. conceived the project and developed the theory. G.J.M., V.V.-H., E.P. and J.P.T. designed the experiment. G.J.M. and V.V.-H. conducted the experiment. A.P., A.C. and M.L. assisted with the theory. E.P. wrote the manuscript, with assistance from V.V.-H. for the Methods section. J.P.T. supervised the experimental work and M.L. oversaw the theory development. All authors contributed to the scientific discussion.

Corresponding author

Correspondence to Emilio Pisanty.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains more information about the work and Supplementary Figs. 1–11.

Supplementary Data 1

3D-printable models of Fig. 1d and e.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pisanty, E., Machado, G.J., Vicuña-Hernández, V. et al. Knotting fractional-order knots with the polarization state of light. Nat. Photonics 13, 569–574 (2019). https://doi.org/10.1038/s41566-019-0450-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41566-019-0450-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing