Abstract
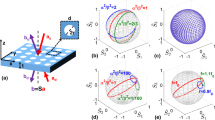
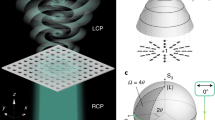
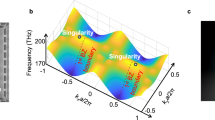
Optical bound states in the continuum (BICs) are states supported by a photonic structure that are compatible with free-space radiation, yet become perfectly bound for one specific in-plane momentum and wavelength1,2. Recently, it was predicted that light radiated by such modes around the BIC momentum–frequency condition should display a vortex in its far-field polarization profile, making the BIC topologically protected3. Here, we study a one-dimensional grating supporting a transverse magnetic mode with a BIC near 700 nm wavelength, verifying the existence of the BIC using reflection measurements, which show a vanishing reflection feature. Using k-space polarimetry, we measure the full polarization state of reflection around the BIC, highlighting the presence of a topological vortex. We use an electromagnetic dipole model to explain the observed BIC through destructive interference between two radiation channels, characteristic of a Friedrich–Wintgen-type BIC4. Our findings shed light on the origin of BICs and verify their topological nature.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
von Neuman, J. & Wigner, E. Uber merkwürdige diskrete Eigenwerte. Uber das Verhalten von Eigenwerten bei adiabatischen Prozessen. Phys. Z. 30, 467–470 (1929).
Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D. & Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 1, 16048 (2016).
Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. Lett. 113, 257401 (2014).
Friedrich, H. & Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 32, 3231–3242 (1985).
Marinica, D. C., Borisov, A. G. & Shabanov, S. V. Bound states in the continuum in photonics. Phys. Rev. Lett. 100, 183902 (2008).
Yang, Y., Peng, C., Liang, Y., Li, Z. & Noda, S. Analytical perspective for bound states in the continuum in photonic crystal slabs. Phys. Rev. Lett. 113, 37401 (2014).
Hsu, C. W. et al. Observation of trapped light within the radiation continuum. Nature 499, 188–191 (2013).
Bulgakov, E. N. & Sadreev, A. F. Bloch bound states in the radiation continuum in a periodic array of dielectric rods. Phys. Rev. A 90, 53801 (2014).
Silveirinha, M. G. Trapping light in open plasmonic nanostructures. Phys. Rev. A 89, 23813 (2014).
Monticone, F., & Alù, A. Embedded photonic eigenvalues in 3D nanostructures. Phys. Rev. Lett. 112, 213903 (2014).
Kodigala, A. et al. Lasing action from photonic bound states in continuum. Nature 541, 196–199 (2017).
Yanik, A. A. et al. Seeing protein monolayers with naked eye through plasmonic Fano resonances. Proc. Natl Acad. Sci. USA 108, 11784–11789 (2011).
Foley, J. M., Young, S. M. & Phillips, J. D. Symmetry-protected mode coupling near normal incidence for narrow-band transmission filtering in a dielectric grating. Phys. Rev. B 89, 165111 (2014).
Plotnik, Y. et al. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 107, 183901 (2011).
Sakoda, K. Optical Properties of Photonic Crystals 80 (Springer, Berlin, 2005).
Lieb, M. A., Zavislan, J. M. & Novotny, L. Single-molecule orientations determined by direct emission pattern imaging. J. Opt. Soc. Am. B 21, 1210 (2004).
Fallet, C. Angle Resolved Mueller Polarimetry, Applications to Periodic Structures. PhD thesis, Ecole Polytechnique X (2011).
Sersic, I., Tuambilangana, C. & Femius Koenderink, A. Fourier microscopy of single plasmonic scatterers. New J. Phys. 13, 83019 (2011).
Kurvits, J. A., Jiang, M. & Zia, R. Comparative analysis of imaging configurations and objectives for Fourier microscopy. J. Opt. Soc. Am. A 32, 2082 (2015).
Osorio, C. I., Mohtashami, A. & Koenderink, A. F. K-space polarimetry of bullseye plasmon antennas. Sci. Rep. 5, 9966 (2015).
Lepetit, T. & Kanté, B. Controlling multipolar radiation with symmetries for electromagnetic bound states in the continuum. Phys. Rev. B 90, 241103 (2014).
Rybin, M. V. et al. High-Q supercavity modes in subwavelength dielectric resonators. Phys. Rev. Lett. 119, 243901 (2017).
Acknowledgements
This work is part of the research programme of the Netherlands Organisation for Scientific Research (NWO) and was performed at the research institute AMOLF. The authors thank R. Struik for the design used in Fig. 1. A.A. and F.M. acknowledge support from the Air Force Office of Scientific Research (MURI grant no. FA9550-17-1-0002), the Simons Foundation, the National Science Foundation and the Welch Foundation (grant no. F-1802).
Author information
Authors and Affiliations
Contributions
F.M., A.A. and A.F.K. initiated the research project, and A.A. and A.F.K. supervised throughout the project. All reflection and polarimetry experiments, as well as their analysis, were carried out by H.M.D., under the supervision of A.F.K. RCWA and full-wave simulations were performed by F.M. Dipole model calculations were carried out by H.M.D. and F.M. Sample fabrication and calibration of the experimental set-up were done by W.d.H. All authors discussed the results and were involved in writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary discussion; Supplementary Figures 1–10; Supplementary References 1–8.
Supplementary Video 1
Reflection, vertical polarization.
Supplementary Video 2
Reflection, horizontal polarization.
Supplementary Video 3
Eigenmode field distribution.
Rights and permissions
About this article
Cite this article
Doeleman, H.M., Monticone, F., den Hollander, W. et al. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nature Photon 12, 397–401 (2018). https://doi.org/10.1038/s41566-018-0177-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0177-5
This article is cited by
-
Reconfigurable quantum fluid molecules of bound states in the continuum
Nature Physics (2024)
-
Linear and phase controllable terahertz frequency conversion via ultrafast breaking the bond of a meta-molecule
Nature Communications (2024)
-
Vortex nanolaser based on a photonic disclination cavity
Nature Photonics (2024)
-
Design and analysis of a flexible Ruddlesden–Popper 2D perovskite metastructure based on symmetry-protected THz-bound states in the continuum
Scientific Reports (2023)
-
Nonlocal flat optics
Nature Photonics (2023)