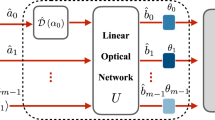
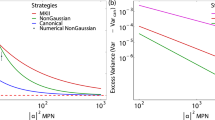
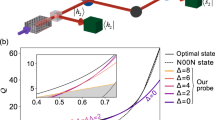
Abstract
Interferometric phase measurement is widely used to precisely determine quantities such as length, speed and material properties1,2,3. Without quantum correlations, the best phase sensitivity \({\boldsymbol{\Delta }}{\boldsymbol{\phi }}\) achievable using n photons is the shot-noise limit, \({\boldsymbol{\Delta }}{\boldsymbol{\phi }}=1\,/\sqrt{{n}}\). Quantum-enhanced metrology promises better sensitivity, but, despite theoretical proposals stretching back decades3,4, no measurement using photonic (that is, definite photon number) quantum states has truly surpassed the shot-noise limit. Instead, all such demonstrations, by discounting photon loss, detector inefficiency or other imperfections, have considered only a subset of the photons used. Here, we use an ultrahigh-efficiency photon source and detectors to perform unconditional entanglement-enhanced photonic interferometry. Sampling a birefringent phase shift, we demonstrate precision beyond the shot-noise limit without artificially correcting our results for loss and imperfections. Our results enable quantum-enhanced phase measurements at low photon flux and open the door to the next generation of optical quantum metrology advances.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Wiseman, H. M. & Milburn, G. J. Quantum Measurement and Control (Cambridge Univ. Press, 2009).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222–229 (2011).
Demkowicz-Dobrzański, R., Jarzyna, M. & Kołdyński, J. Chapter four-quantum limits in optical interferometry. Prog. Opt. 60, 345–435 (2015).
Dowling, J. P. Quantum optical metrology—the lowdown on high-NOON states. Contemp. Phys. 49, 125–143 (2008).
Wolfgramm, F., Vitelli, C., Beduini, F. A., Godbout, N. & Mitchell, M. W. Entanglement-enhanced probing of a delicate material system. Nat. Photon. 7, 28–32 (2013).
Yonezawa, H. et al. Quantum-enhanced optical-phase tracking. Science 337, 1514–1517 (2012).
Aasi, J. et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photon. 7, 613–619 (2013).
Xiang, G., Hofmann, H. & Pryde, G. J. Optimal multi-photon phase sensing with a single interference fringe. Sci. Rep. 3, 2684 (2013).
Resch, K. J. et al. Time-reversal and super-resolving phase measurements. Phys. Rev. Lett. 98, 223601 (2007).
Ou, Z. Y., Zou, X. Y., Wang, L. J. & Mandel, L. Experiment on nonclassical fourth-order interference. Phys. Rev. A 42, 2957–2965 (1990).
Rarity, J. G. et al. Two-photon interference in a Mach–Zehnder interferometer. Phys. Rev. Lett. 65, 1348–1351 (1990).
Fonseca, E. J. S., Monken, C. H. & Pádua, S. Measurement of the de Broglie wavelength of a multiphoton wave packet. Phys. Rev. Lett. 82, 2868–2871 (1999).
Eisenberg, H. S., Hodelin, J. F., Khoury, G. & Bouwmeester, D. Multiphoton path entanglement by nonlocal bunching. Phys. Rev. Lett. 94, 090502 (2005).
Mitchell, M. W., Lundeen, J. S. & Steinberg, A. M. Super-resolving phase measurements with a multiphoton entangled state. Nature 429, 161–164 (2004).
Walther, P. et al. De Broglie wavelength of a non-local four-photon state. Nature 429, 158–161 (2004).
Nagata, T., Okamoto, R., O’Brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007).
Gao, W.-B. et al. Experimental demonstration of a hyper-entangled ten-qubit Schrödinger cat state. Nat. Phys. 6, 331–335 (2010).
Wang, X.-L. et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 117, 210502 (2016).
Okamoto, R. et al. Beating the standard quantum limit: phase super-sensitivity of N-photon interferometers. New J. Phys. 10, 073033 (2008).
Datta, A. et al. Quantum metrology with imperfect states and detectors. Phys. Rev. A 83, 063836 (2011).
Weston, M. M. et al. Efficient and pure femtosecond-pulse-length source of polarization-entangled photons. Opt. Express 24, 10869–10879 (2016).
Marsili, F. et al. Detecting single infrared photons with 93% system efficiency. Nat. Photon. 7, 210–214 (2013).
Klyshko, D. N. Use of two-photon light for absolute calibration of photoelectric detectors. Sov. J. Quantum Electron. 10, 1112–1116 (1980).
Lita, A. E., Miller, A. J. & Nam, S. W. Counting near-infrared single-photons with 95% efficiency. Opt. Express 16, 3032–3040 (2008).
Matthews, J. C. F. et al. Towards practical quantum metrology with photon counting. NPJ Quantum Inf. 2, 16023 (2016).
Harder, G. et al. Single-mode parametric-down-conversion states with 50 photons as a source for mesoscopic quantum optics. Phys. Rev. Lett. 116, 143601 (2016).
Higgins, B. L., Berry, D. W., Bartlett, S. D., Wiseman, H. M. & Pryde, G. J. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393–396 (2007).
Davison, A. C. & Hinkley, D. V. Bootstrap Methods and Their Application, Vol. 1 (Cambridge Univ. Press, 1997).
Acknowledgements
This work was supported by the Australian Research Council (grant DP140100648). The authors thank J. Ho for help with SNSPDs.
Author information
Authors and Affiliations
Contributions
G.J.P. conceived the idea and supervised the project. S.S. and M.M.W. constructed and carried out the experiment with help from H.M.C. L.K.S., V.B.V. and S.W.N. developed the high-efficiency SNSPDs. All authors discussed the results and contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Slussarenko, S., Weston, M.M., Chrzanowski, H.M. et al. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nature Photon 11, 700–703 (2017). https://doi.org/10.1038/s41566-017-0011-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-017-0011-5
This article is cited by
-
Distributed quantum sensing of multiple phases with fewer photons
Nature Communications (2024)
-
Applications of single photons in quantum metrology, biology and the foundations of quantum physics
Nature Reviews Physics (2023)
-
Experimental metrology beyond the standard quantum limit for a wide resources range
npj Quantum Information (2023)
-
Resolution of 100 photons and quantum generation of unbiased random numbers
Nature Photonics (2023)
-
Approaching optimal entangling collective measurements on quantum computing platforms
Nature Physics (2023)