Abstract
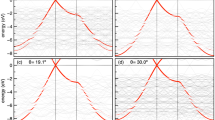
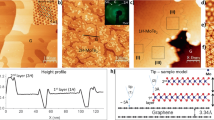
Two-dimensional (2D) heterostructures assembled via van der Waals (vdW) interactions have sparked immense interest in fields from physics1,2 to electronics3,4. Understanding the vdW interaction at these heterointerfaces is critical for the sophisticated construction and manipulation of these 2D heterostructures. However, previous experimental research has mainly focused on the interlayer interactions in homogeneous graphite crystals5,6 and the interactions between graphene and substrates7. Theoretically, although a variety of vdW methods have been incorporated in density functional theory to probe the interactions of homogeneous vdW crystals, the reliability of these vdW methods in 2D heterostructures remains to be verified. Here, we show, by contact-splitting transfer of graphite from hexagonal boron nitride (BN) to molybdenum disulfide (MoS2), that graphite experiences a stronger vdW interaction with MoS2 than with boron nitride. Quantitative measurements using a graphite-wrapped atomic force microscope tip show that the critical adhesion pressures between BN and graphite and MoS2 and graphite are respectively 0.953 and 1.028 times that between graphite and graphite. The results are consistent with the prediction based on Lifshitz theory, implying an important role of material dielectric function in the vdW interactions at heterointerfaces. These findings offer us more freedom in the construction of 2D heterostructures, and a technique to disassemble 2D heterostructures is demonstrated.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Dean, C. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moire superlattices. Nature 497, 598–602 (2013).
Kumar, R. K. et al. High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181–184 (2017).
Liu, Y. et al. Van der Waals heterostructures and devices. Nat. Rev. Mater. 1, 16042 (2016).
Chen, S. et al. Electron optics with pn junctions in ballistic graphene. Science 353, 1522–1525 (2016).
Liu, Z. et al. Interlayer binding energy of graphite: a mesoscopic determination from deformation. Phys. Rev. B 85, 205418 (2012).
Koren, E., Lörtscher, E., Rawlings, C., Knoll, A. W. & Duerig, U. Adhesion and friction in mesoscopic graphite contacts. Science 348, 679–683 (2015).
Koenig, S. P., Boddeti, N. G., Dunn, M. L. & Bunch, J. S. Ultrastrong adhesion of graphene membranes. Nat. Nanotechnol. 6, 543–546 (2011).
Ishigami, M., Chen, J., Cullen, W., Fuhrer, M. & Williams, E. Atomic structure of graphene on SiO2. Nano Lett. 7, 1643–1648 (2007).
Wang, W. et al. Measurement of the cleavage energy of graphite. Nat. Commun. 6, 7853 (2015).
Cuenot, S., Fretigny, C., Demoustier-Champagne, S. & Nysten, B. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy. Phys. Rev. B 69, 165410 (2004).
Gould, T. et al. Binding and interlayer force in the near-contact region of two graphite slabs: experiment and theory. J. Chem. Phys. 139, 224704 (2013).
You, Y., Ni, Z., Yu, T. & Shen, Z. Edge chirality determination of graphene by Raman spectroscopy. Appl. Phys. Lett. 93, 163112 (2008).
Pizzocchero, F. et al. The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat. Commun. 7, 11894 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Tkatchenko, A., DiStasio, R. A. Jr, Car, R. & Scheffler, M. Accurate and efficient method for many-body van der Waals interactions. Phys. Rev. Lett. 108, 236402 (2012).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 132, 154104 (2010).
Dion, M., Rydberg, H., Schröder, E., Langreth, D. C. & Lundqvist, B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401 (2004).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201 (2009).
Tkatchenko, A. & Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009).
Marom, N. et al. Many-body dispersion interactions in molecular crystal polymorphism. Angew. Chem. Int. Ed. 52, 6629–6632 (2013).
Gao, W. & Tkatchenko, A. Electronic structure and van der Waals interactions in the stability and mobility of point defects in semiconductors. Phys. Rev. Lett. 111, 045501 (2013).
Liu, X., Hermann, J. & Tkatchenko, A. Communication: many-body stabilization of non-covalent interactions. Structure, stability, and mechanics of Ag3Co(CN)6 framework. J. Chem. Phys. 145, 241101 (2016).
Sapnik, A. et al. Uniaxial negative thermal expansion and metallophilicity in Cu3[Co(CN)6]. J. Solid State Chem. 258, 298–306 (2018).
Tkatchenko, A., Rossi, M., Blum, V., Ireta, J. & Scheffler, M. Unraveling the stability of polypeptide helices: critical role of van der Waals interactions. Phys. Rev. Lett. 106, 118102 (2011).
Björkman, T., Gulans, A., Krasheninnikov, A. & Nieminen, R. Are we van der Waals ready? J. Phys. Condens. Matter 24, 424218 (2012).
Sarabadani, J., Naji, A., Asgari, R. & Podgornik, R. Many-body effects in the van der Waals–Casimir interaction between graphene layers. Phys. Rev. B 84, 155407 (2011).
Lifshitz, E. The theory of molecular attractive forces between solids. Sov. Phys. JETP 2, 73–83 (1956).
Harl, J. & Kresse, G. Cohesive energy curves for noble gas solids calculated by adiabatic connection fluctuation-dissipation theory. Phys. Rev. B 77, 045136 (2008).
Parsegian, V. A. in Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists Ch. 2 (Cambridge Univ. Press, 2005).
Kumar, A. & Ahluwalia, P. K. Tunable dielectric response of transition metals dichalcogenides MX2 (M = Mo, W; X = S, Se, Te): effect of quantum confinement. Physica B Phys. Condens. Matter 407, 4627–4634 (2012).
Acknowledgements
This work was supported by the NSF of China (grants nos. 51535005, 11702132, 51472117 and 51702159) and NSF of Jiangsu Province (grants nos. BK20170770 and BK20170791). The authors also acknowledge support from the China Postdoctoral Science Foundation (grants nos. 2016M600408, 2017T100362 and 2017M610328), Jiangsu Postdoctoral Research Funds (no. 1701141B), the Fundamental Research Funds for the Central Universities (no. NC2018001) and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Author information
Authors and Affiliations
Contributions
W.G., J.Y. and B.L. designed the experimental strategy. B.L., J.Y. and H.W. performed the experiments. X. Liu designed and performed the theoretical study. All authors contributed to the analysis and discussion. W.G., B.L., J.Y. and X. Liu wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information Nature Nanotechnology thanks José María Gomez-Rodriguez, Kian Ping Loh and other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Methods, Results, Fig. 1–8 and Table 1.
Rights and permissions
About this article
Cite this article
Li, B., Yin, J., Liu, X. et al. Probing van der Waals interactions at two-dimensional heterointerfaces. Nat. Nanotechnol. 14, 567–572 (2019). https://doi.org/10.1038/s41565-019-0405-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-019-0405-2
This article is cited by
-
Variant Plateau’s law in atomically thin transition metal dichalcogenide dome networks
Nature Communications (2023)
-
Enhanced osmotic transport in individual double-walled carbon nanotube
Nature Communications (2023)
-
Mechanics of 2D material bubbles
Nano Research (2023)
-
Determining the interlayer shearing in twisted bilayer MoS2 by nanoindentation
Nature Communications (2022)
-
Interlayer shear coupling in bilayer graphene
npj 2D Materials and Applications (2022)