Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Robust topologically protected transport in photonic crystals at telecommunication wavelengths

Nature Nanotechnology volume 14, pages 31–34 (2019)Cite this article

Subjects

An Author Correction to this article was published on 17 December 2018

This article has been updated

Abstract

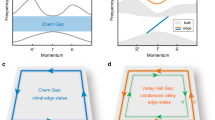
Photonic topological insulators offer the possibility to eliminate backscattering losses and improve the efficiency of optical communication systems. Despite considerable efforts, a direct experimental demonstration of theoretically predicted robust, lossless energy transport in topological insulators operating at near-infrared frequencies is still missing. Here, we combine the properties of a planar silicon photonic crystal and the concept of topological protection to design, fabricate and characterize an optical topological insulator that exhibits the valley Hall effect. We show that the transmittances are the same for light propagation along a straight topological interface and one with four sharp turns. This result quantitatively demonstrates the suppression of backscattering due to the non-trivial topology of the structure. The photonic-crystal-based approach offers significant advantages compared with other realizations of photonic topological insulators, such as lower propagation losses, the presence of a band gap for light propagating in the crystal-slab plane, a larger operating bandwidth, a much smaller footprint, compatibility with complementary metal–oxide–semiconductor fabrication technology, and the fact that it allows for operation at telecommunications wavelengths.

Your institute does not have access to this article

Relevant articles

Open Access articles citing this article.

Access options

Buy article

Get time limited or full article access on ReadCube.

$32.00

Buy

All prices are NET prices.

Fig. 1: Schematic and operation principles of the photonic-crystal-based topological insulator.
Fig. 2: Scattering-free edge state in the photonic-crystal-based topological insulator.
Fig. 3: Observation of topologically protected propagation in a photonic-crystal-based topological insulator.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Change history

  • 17 December 2018

    In the version of this Letter originally published, Fig. 5g in the Supplementary Information was missing the scale bar. This has now been corrected.

References

  1. Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).

    CAS  Article  Google Scholar 

  2. Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).

    CAS  Article  Google Scholar 

  3. Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).

    CAS  Article  Google Scholar 

  4. Bernevig, A. B. & Hughes, T. L. Topological Insulators and Topological Superconductors (Princeton Univ. Press, Princeton, 2013).

  5. Ferreira, G. J. & Loss, D. Magnetically defined qubits on 3D topological insulators. Phys. Rev. Lett. 111, 106802 (2013).

    Article  Google Scholar 

  6. Katmis, F. et al. A high-temperature ferromagnetic topological insulating phase by proximity coupling. Nature 533, 513–516 (2016).

    CAS  Article  Google Scholar 

  7. Jotzu, G. et al. Experimental realization of the topological haldane model with ultracold fermions. Nature 515, 237–240 (2014).

    CAS  Article  Google Scholar 

  8. Lu, J. et al. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 13, 369–375 (2016).

    Article  Google Scholar 

  9. Umucalılar, R. O. & Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 84, 043804 (2011).

    Article  Google Scholar 

  10. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).

    CAS  Article  Google Scholar 

  11. Khanikaev, A. B. et al. Photonic topological insulators. Nat. Mater. 12, 233–239 (2012).

    Article  Google Scholar 

  12. Fang, K. J., Yu, Z. F. & Fan, S. H. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).

    CAS  Article  Google Scholar 

  13. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).

    CAS  Article  Google Scholar 

  14. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    CAS  Article  Google Scholar 

  15. Barik, S. et al. A topological quantum optics interface. Science 359, 666–668 (2018).

    CAS  Article  Google Scholar 

  16. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    CAS  Article  Google Scholar 

  17. Mittal, S. et al. Topologically robust transport of photons in a synthetic gauge field. Phys. Rev. Lett. 113, 087403 (2014).

    CAS  Article  Google Scholar 

  18. Chen, W. J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 5782 (2014).

    CAS  Article  Google Scholar 

  19. Ma, T., Khanikaev, A. B., Mousavi, S. H. & Shvets, G. Guiding electromagnetic waves around sharp corners: topologically protected photonic transport in metawaveguides. Phys. Rev. Lett. 114, 127401 (2015).

    Article  Google Scholar 

  20. Ma, T. & Shvets, G. Scattering-free edge states between heterogeneous photonic topological insulators. Phys. Rev. B 95, 165102 (2017).

    Article  Google Scholar 

  21. Wu, X. et al. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals. Nat. Commun. 8, 1304 (2017).

    Article  Google Scholar 

  22. Wu, L. H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).

    Article  Google Scholar 

  23. Ma, T. & Shvets, G. All-Si valley-Hall photonic topological insulator. New J. Phys. 18, 025012 (2016).

    Article  Google Scholar 

  24. Chen, X.-D., Zhao, F.-L., Chen, M. & Dong, J.-W. Valley-contrasting physics in all-dielectric photonic crystals: orbital angular momentum and topological propagation. Phys. Rev. B 96, 020202 (2017).

    Article  Google Scholar 

  25. Dong, J.-W., Chen, X.-D., Zhu, H., Wang, Y. & Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 16, 298–302 (2016).

    Article  Google Scholar 

  26. He, X.-T. et al. Silicon-on-insulator slab for topological valley transport. Preprint at https://arxiv.org/abs/1805.10962 (2018).

  27. Dulkeith, E., McNab, S. J. & Vlasov, Y. A. Mapping the optical properties of slab-type two-dimensional photonic crystal waveguides. Phys. Rev. B 72, 115102 (2005).

    Article  Google Scholar 

  28. Joannopoulos, J. D., Johnson, S. G., Winn, J. N. & Meade, R. D. Photonic Crystals Molding the Flow of Light 2nd edn (Princeton Univ. Press, Princeton, 2008).

  29. Collins, M. J., Zhang, F., Bojko, R., Chrostowski, L. & Rechtsman, M. C. Integrated optical Dirac physics via inversion symmetry breaking. Phys. Rev. A. 94, 063827 (2016).

    Article  Google Scholar 

  30. Barik, S., Miyake, H., DeGottardi, W., Waks, E. & Hafezi, M. Two-dimensionally confined topological edge states in photonic crystals. New J. Phys. 18, 113013 (2016).

    Article  Google Scholar 

  31. Fukui, T., Hatsugai, Y. & Suzuki, H. Chern numbers in discretized Brillouin zone: efficient method of computing (spin) Hall conductances. J. Phys. Soc. Jpn 74, 1674–1677 (2005).

    CAS  Article  Google Scholar 

  32. Bleu, O., Solnyshkov, D. D. & Malpuech, G. Quantum valley Hall effect and perfect valley filter based on photonic analogs of transitional metal dichalcogenides. Phys. Rev. B 95, 235431 (2017).

    Article  Google Scholar 

  33. Shalaev, M. I., Desnavi, S., Walasik, W. & Litchinitser, N. M. Reconfigurable topological photonic crystal. New J. Phys. 20, 023040 (2018).

    Article  Google Scholar 

  34. Reardon, C. P., Rey, I. H., Welna, K., O'Faolain, L. & Krauss, T. F. Fabrication and characterization of photonic crystal slow light waveguides and cavities. J. Vis. Exp. 69, e50216 (2012).

    Google Scholar 

Download references

Acknowledgements

This work was supported by Army Research Office grants W911NF-15-1-0152 and W911NF-11-1-0297. The authors acknowledge discussions with A. Khanikaev.

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, Duke University, Durham, NC, USA

    Mikhail I. Shalaev, Wiktor Walasik, Yun Xu & Natalia M. Litchinitser

  2. Toronto Nanofabrication Centre, University of Toronto, Toronto, Ontario, Canada

    Alexander Tsukernik

  3. Department of Electrical Engineering, University at Buffalo, The State University of New York, Buffalo, NY, USA

    Yun Xu

Authors
  1. Mikhail I. Shalaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wiktor Walasik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alexander Tsukernik
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yun Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Natalia M. Litchinitser
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.I.S. and N.M.L. proposed the initial idea. M.I.S. and W.W. designed and performed the analytical and numerical analysis of the structure. M.I.S. fabricated the sample, performed the experimental measurements and analysed the results. A.T. and Y.X. assisted with the fabrication and measurement process of the sample. W.W., M.I.S. and N.M.L. co-wrote the manuscript. N.M.L. supervised the work.

Corresponding author

Correspondence to Natalia M. Litchinitser.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information

Supplementary Sections A–D

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Shalaev, M.I., Walasik, W., Tsukernik, A. et al. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nature Nanotech 14, 31–34 (2019). https://doi.org/10.1038/s41565-018-0297-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41565-018-0297-6

Further reading

Search

Advanced search

Quick links

Find nanotechnology articles, nanomaterial data and patents all in one place. Visit Nano by Nature Research