Abstract
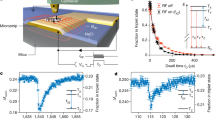
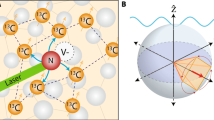
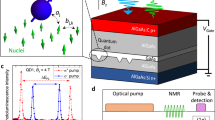
Nuclear spins serve as sensitive probes in chemistry1 and materials science2 and are promising candidates for quantum information processing3,4,5,6. NMR, the resonant control of nuclear spins, is a powerful tool for probing local magnetic environments in condensed matter systems, which range from magnetic ordering in high-temperature superconductors7,8 and spin liquids9 to quantum magnetism in nanomagnets10,11. Increasing the sensitivity of NMR to the single-atom scale is challenging as it requires a strong polarization of nuclear spins, well in excess of the low polarizations obtained at thermal equilibrium, as well as driving and detecting them individually4,5,12. Strong nuclear spin polarization, known as hyperpolarization, can be achieved through hyperfine coupling with electron spins2. The fundamental mechanism is the conservation of angular momentum: an electron spin flips and a nuclear spin flops. The nuclear hyperpolarization enables applications such as in vivo magnetic resonance imaging using nanoparticles13, and is harnessed for spin-based quantum information processing in quantum dots14 and doped silicon15,16,17. Here we polarize the nuclear spins of individual copper atoms on a surface using a spin-polarized current in a scanning tunnelling microscope. By employing the electron–nuclear flip-flop hyperfine interaction, the spin angular momentum is transferred from tunnelling electrons to the nucleus of individual Cu atoms. The direction and magnitude of the nuclear polarization is controlled by the direction and amplitude of the current. The nuclear polarization permits the detection of the NMR of individual Cu atoms, which is used to sense the local magnetic environment of the Cu electron spin.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Staudacher, T. et al. Nuclear magnetic resonance spectroscopy on a (5-nanometer)3 sample volume. Science 339, 561–563 (2013).
Slichter, C. P. Principles of Magnetic Resonance (Springer, Heidelberg, 1996).
Morley, G. W. et al. Quantum control of hybrid nuclear–electronic qubits. Nat. Mater. 12, 103–107 (2013).
Thiele, S. et al. Electrically driven nuclear spin resonance in single-molecule magnets. Science 344, 1135–1138 (2014).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Sigillito, A. J. et al. All-electric control of donor nuclear spin qubits in silicon. Nat. Nanotech. 12, 958–962 (2017).
Alloul, H., Ohno, T. & Mendels, P. 89Y NMR evidence for a Fermi-liquid behavior in YBa2Cu3O6+x. Phys. Rev. Lett. 63, 1700–1703 (1989).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 477, 191–194 (2011).
Mendels, P. et al. Ga NMR study of the local susceptibility in kagomé-based SrCr8Ga4O19: pseudogap and paramagnetic defects. Phys. Rev. Lett. 85, 3496–3499 (2000).
Borsa, F., Lascialfari, A. & Furukawa, Y. Novel NMR and EPR Techniques (eds Dolinšek, J., Vilfan, M. & Žumer, S.) 297–349 (Springer, Heidelberg, 2006).
Micotti, E. et al. Local spin moment distribution in antiferromagnetic molecular rings probed by NMR. Phys. Rev. Lett. 97, 267204 (2006).
Dutt, M. V. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312–1316 (2007).
Cassidy, M. C. et al. In vivo magnetic resonance imaging of hyperpolarized silicon particles. Nat. Nanotech. 8, 363–368 (2013).
Urbaszek, B. et al. Nuclear spin physics in quantum dots: an optical investigation. Rev. Mod. Phys. 85, 79–133 (2013).
McCamey, D. R., van Tol, J., Morley, G. W. & Boehme, C. Fast nuclear spin hyperpolarization of phosphorus in silicon. Phys. Rev. Lett. 102, 027601 (2009).
Simmons, S. et al. Entanglement in a solid-state spin ensemble. Nature 470, 69–72 (2011).
Morley, G. W. et al. The initialization and manipulation of quantum information stored in silicon by bismuth dopants. Nat. Mater. 9, 725–729 (2010).
Smet, J. H. et al. Gate-voltage control of spin interactions between electrons and nuclei in a semiconductor. Nature 415, 281–286 (2002).
Lo, C. C. et al. All-electrical nuclear spin polarization of donors in silicon. Phys. Rev. Lett. 110, 057601 (2013).
Trowbridge, C. J. et al. Dynamic nuclear polarization from current-induced electron spin polarization. Phys. Rev. B 90, 085122 (2014).
Paul, W. et al. Control of the millisecond spin lifetime of an electrically probed atom. Nat. Phys. 13, 403–407 (2017).
Ting, Y. & Lew, H. Hyperfine structure of Cu63 and Cu65. Phys. Rev. 105, 581–588 (1957).
Heinrich, A. J., Gupta, J. A., Lutz, C. P. & Eigler, D. M. Single-atom spin-flip spectroscopy. Science 306, 466–469 (2004).
Baumann, S. et al. Electron paramagnetic resonance of individual atoms on a surface. Science 350, 417–420 (2015).
Yang, K. et al. Engineering the eigenstates of coupled spin-1/2 atoms on a surface. Phys. Rev. Lett. 119, 227206 (2017).
Willke, P. et al. Hyperfine interaction of individual atoms on a surface. Science 362, 336–339 (2018).
Otte, A. F. et al. The role of magnetic anisotropy in the Kondo effect. Nat. Phys. 4, 847–850 (2008).
McGarvey, B. R. The isotropic hyperfine interaction. J. Phys. Chem. 71, 51–66 (1967).
Loth, S. et al. Controlling the state of quantum spins with electric currents. Nat. Phys. 6, 340–344 (2010).
Reimer, J. A. Nuclear hyperpolarization in solids and the prospects for nuclear spintronics. Solid. State Nucl. Magn. Reson. 37, 3–12 (2010).
Wolfowicz, G. et al. Atomic clock transitions in silicon-based spin qubits. Nat. Nanotech. 8, 561–564 (2013).
Shiddiq, M. et al. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 531, 348–351 (2016).
Heinrich, B. W., Braun, L., Pascual, J. I. & Franke, K. J. Protection of excited spin states by a superconducting energy gap. Nat. Phys. 9, 765–768 (2013).
Acknowledgements
We thank B. Melior for expert technical assistance. We acknowledge financial support from the Office of Naval Research. P.W., Y.B. and A.J.H. acknowledge support from Institute for Basic Science under IBS-R027-D1. P.W. acknowledges support from the Alexander von Humboldt Foundation. A.F. acknowledges CONICET (PIP11220150100327 and PUE-22920170100089CO). J.L.L. thanks the ETH Fellowship program for financial support. J.F.-R. thanks FCT, under the project PTDC/FIS-NAN/4662/2014.
Author information
Authors and Affiliations
Contributions
K.Y. and C.P.L. designed the experiment. K.Y., P.W. and Y.B. carried out the STM measurements. K.Y. and C.P.L. performed the analysis and developed the rate equation model. A.F., J.L.L. and J.F.-R. performed the DFT calculations. All the authors discussed the results and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–6
Rights and permissions
About this article
Cite this article
Yang, K., Willke, P., Bae, Y. et al. Electrically controlled nuclear polarization of individual atoms. Nature Nanotech 13, 1120–1125 (2018). https://doi.org/10.1038/s41565-018-0296-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-018-0296-7
This article is cited by
-
Universal quantum control of an atomic spin qubit on a surface
npj Quantum Information (2023)
-
Electron spin resonance of single iron phthalocyanine molecules and role of their non-localized spins in magnetic interactions
Nature Chemistry (2022)
-
Enhanced conductance response in radio frequency scanning tunnelling microscopy
Scientific Reports (2022)
-
Trends in the hyperfine interactions of magnetic adatoms on thin insulating layers
npj Computational Materials (2021)
-
Light–matter interaction at atomic scales
Nature Reviews Physics (2021)