Main

Microbial pathogens are responsible for more than 400 million years of life lost annually across the globe, a higher burden than either cancer or cardiovascular disease1. Diseases that have long plagued humanity, such as malaria and tuberculosis, continue to impose a staggering toll. Recent decades have also witnessed the emergence of new virulent pathogens, including human immunodeficiency virus (HIV), Ebola virus, severe acute respiratory syndrome (SARS) coronavirus, West Nile virus and Zika virus.

The persistent global threat posed by microbial pathogens arises from the nonlinear mechanisms of disease transmission. That is, as the prevalence of a disease is reduced, the density of immune individuals drops, the density of susceptible individuals rises and disease is more likely to rebound. The resultant temporal trajectories are difficult to predict without considering this nonlinear interplay. For instance, many microbial diseases exhibit periodic spikes in the number of cases that are unexplainable by pathogen natural history or environmental phenomena. By explicitly defining the nonlinear processes underlying infectious disease spread, transmission models illuminate these otherwise opaque systems.

Forty years ago, Nature published a series of papers that launched the modern era of infectious disease modelling2,3. Since that time, these methodologies have multiplied4. Transmission models now employ a variety of approaches, ranging from agent-based simulations that represent each individual5 to compartmental frameworks that group individuals by epidemiological status, such as infectiousness and immunity2,3. Accompanying the methodological innovations, however, are challenges regarding selection of appropriate model structures from among the wealth of possibilities6.

At this anniversary of the publication of these landmark papers2,3, we reflect on contributions that transmission modelling has made to infectious disease science and control. Through a series of case studies, we illustrate the overarching principles and challenges related to model design. With expanding computational capacity and new types of data, myriad opportunities have opened for transmission modelling to bolster evidence-based policy (Box 1)7,8. In all pursuits, modelling is most informative when conducted collaboratively with microbiologists, immunologists and epidemiologists. We offer this Perspective as an entry point for non-modelling scientists to understand the power and flexibility of modelling, and as a foundation for the transdisciplinary conversations that bolster the field.

Modelling across scales

Even within the same disease system, the ideal model design depends on the specifics of the questions asked. Here, we highlight a series of models focused on one of the defining infectious agents of our era: HIV. The virus has challenged science, medicine and public health at every scale, from its deft immune evasion to its death toll of more than 35 million over the last four decades9. We describe how clinical needs, research questions and data availability have shaped the design of HIV models across these scales. Unless otherwise indicated, the term ‘HIV’ is inclusive of both HIV-1 and HIV-2.

Within-host models

At a within-host scale (Table 1), models can be used to simulate cellular interactions, immunological responses and treatment pharmacokinetics10. In such simulations, viral dynamics are often modelled using a compartmental structure, with the growth of one population, such as circulating virions, dependent on the size of another population, such as infected cells. For example, a seminal within-host model fit to viral load data by Perelson et al.11 revealed high turnover rates of HIV-1, counter to what was then the prevailing assumption that HIV-1 remained dormant during the asymptomatic ‘latency’ phase. The corollary to these high rates of viral turnover was that drug resistance would likely evolve rapidly under monotherapy. Further analyses of this model indicated that a combination of at least three drugs was necessary to maintain drug sensitivity12. Once combination therapy did become available, extension of the Perelson et al. model demonstrated that the two-phase decline in viral load observed following treatment initiation was attributable to a reservoir of long-lived infected cells13. With this insight also came the realization that prolonged treatment would be necessary to suppress viral load. The incorporation of stochasticity into this within-host framework allowed model fitting to ‘viral blips’—transient peaks in viral load, even under antiretroviral treatment14. Analysis of this data-driven stochastic model demonstrated that homeostatic proliferation maintained the infected cell reservoir and produced these viral blips, a finding that was later confirmed experimentally15,16. The implication for clinical care was that intensified antiretroviral treatment would be unable to eliminate the latent reservoir of infected cells as had been hypothesized, sparing patients from potentially fruitless trials with such regimens.

Table 1 Scales of modelling for the HIV epidemic
Full size table

Individual-based models

Whereas the unit of interest for within-host modelling is an infected cell, the analogous unit for individual-based models is an infected person (Table 1)5,17,18. Individual-based models are often used to explore the interplay between disease transmission and individual-level risk factors, such as comorbidities, sexual behaviours and age. Such models are capable of incorporating data with individual-level granularity, including those regarding contact patterns, patient treatment cascades and clinical outcomes. Individual-based models are uniquely suited for representing overlap in individual-level risk factors and translating the implications of this overlap for public health policy. For example, an individual-based model was recently used to demonstrate that the majority of HIV transmission among people who inject drugs in New York City is attributable to undiagnosed infections18. These modelling results underscore the urgency for the city to invest in more comprehensive screening and improved diagnostic practices.

Population models

Most commonly, models are created at the population scale, capturing the spread of a pathogen through a large group (Table 1). At this scale, compartmental models shift in focus from the pathogen to the host. Unlike individual-based models, compartmental models will aggregate individuals with a similar epidemiological status. For instance, the archetypical ‘S–I–R’ model separates the entire population of interest into one of three categories: S, susceptible to infection; I, infected and infectious; or R, recovered and protected19. In practice, most models will have additional compartments or stratification beyond this simple structure. Age stratification is essential when either the disease risk or the intervention is age-specific. As an example, an age-stratified multi-pathogen model demonstrated that schistosomiasis prevention targeted to Zimbabwean schoolchildren could cost-effectively reduce HIV acquisition later in life20. This framework was extended to additional countries with a range of age-specific disease prevalence and co-infection rates to assess the potential value of treating schistosomiasis in adults. Although adult treatment is not usually considered efficient, the model showed that it could be cost-effective in settings with high HIV prevalence21. These models strengthened the investment case for treatment of schistosomiasis, an otherwise neglected tropical disease.

Network models are also deployed to represent dynamics on the population scale (Table 1). These models impose a structure on contacts between hosts, unlike compartmental models which assume that contacts are random among hosts within a compartment. In a network model, nodes represent individuals and the connections between nodes represent contacts through which infection may spread22. Sources for network parameterization may include surveys, partner notification services or phylogenetic tracing23,24. As with individual-based models, network models tend to require significant amounts of data to fully parameterize, but various computational and statistical methods have been developed to analyse the impact of uncertain parameter values on model predictions25. Network models are applied to discern the influence of contact structure on disease transmission and on the effectiveness of targeted intervention strategies. For instance, network models predicted that HIV would spread more quickly through sexual partnerships that are concurrent versus serially monogamous, even if the total numbers of sexual acts and partners remain constant26. The study prompted a more rigorous engagement of epidemiologists with sociological data to tailor interventions for specific settings27. Other network models have focused on the more rapid transmission within clusters of high-risk individuals and slower transmission to lower-risk clusters, a dynamic which explains discrepancies between observed incidence patterns and the expected pattern based on an assumption of homogeneous risks28. These studies both illustrate the importance of accounting for network-driven dynamics when individuals are highly aggregated with regards to their risk factors, and when appropriate data for parameterization are available.

Metapopulation models

Metapopulation models represent disease transmission at dual scales, considering not just the interactions of individuals, but also the relationships between groups of individuals, which are typically defined geographically (Table 1). Transmission intensity is often higher within groups than across groups, especially when the groups are spatially segregated29. One metapopulation model of HIV in mainland China considered transmission within and between provinces, driven by the mobility of migrant labourers30. The study suggested that HIV prevention resources could be most effectively targeted to provinces with the greatest initial incidence, as rising incidence in other provinces is driven more by migration from the high-burden provinces than by local transmission. Given that the Chinese provinces with employment opportunities for migrants are also those with the heaviest burden of HIV, migrant workers who acquire HIV often do so in the province where they work. However, government policy requires migrants to return to their home province for treatment. The movement of these workers perpetuates the disease cycle, as new migrants move to fill the vacated jobs and themselves become exposed to elevated HIV risk. These results therefore call for reconsideration of provincial treatment restrictions.

Multinational models

Global policies, such as the treatment goals set by the Joint United Nations Programme on HIV/AIDS (UNAIDS), have been modelled on a global scale (Table 1) by considering the effectiveness of the policies for each nation. For example, a compartmental model was used to evaluate the potential impact of a partially efficacious HIV vaccine on the epidemiological trajectories in 127 countries that together constitute over 99% of the global burden31. The model was tailored to each country by fitting to country-specific incidence trends as well as diagnosis, treatment and viral suppression data. This model revealed that, even with efficacy as low as 50%, a HIV vaccine would avert millions of new infections worldwide, irrespective of whether ambitious treatment goals are met. These results identify the synergies between vaccination and treatment-as-prevention, and provide evidence to support continued investment in vaccine development9,32.

From the cellular level to the population level, HIV modelling has led to improvements in drug formulations, clinical care and resource allocation. As scientific advances continue to bring pharmaceutical innovations, modelling will remain a useful tool for illuminating transmission dynamics and optimizing public health policy.

Modelling emerging and re-emerging pathogens

HIV was not controlled before it became a pandemic, but our response to future outbreaks has the potential to be more timely33. When diseases emerge in new settings, such as Ebola in West Africa and SARS in China, modelling can be rapidly deployed to inform and support response efforts (Fig. 1). Unfortunately, the urgency of public health decisions during such outbreaks tends to be accompanied by a sparsity of data with which to parameterize, calibrate and validate models. As detailed below, uncertainty analysis—a method of analysing how uncertainty in input parameters translates to uncertainty in model outcome variables—becomes all the more vital in these situations. Media attention regarding model predictions is often heightened during outbreaks, ironically at a time when modelling results are apt to be less robust than for well-characterized endemic diseases. We discuss the importance of careful communication regarding model recommendations and associated uncertainty to inform the public without fuelling excessive alarm. Despite these challenges, and especially if these challenges can be navigated, the timely assessment of a wide range of intervention scenarios made possible by modelling would be particularly valuable during infectious disease emergencies.

Fig. 1: Data-driven model prediction to evaluate the impact of manipulatable policy variables.
figure 1

a, Data from a variety of sources, including surveillance reports, experiments and epidemiological studies, can inform model parameters. b, Rather than extracting single point estimates, modellers can use data more powerfully by constructing data-driven distributions for parameters from which values are sampled for each simulation. c, Every simulation yields a projection, such that multiple runs based on drawing probabilistically from empirical distributions generate a probabilistic distribution of projections. Types of projection that can be generated include outbreak trajectories, disease burdens and economic impact. d, Probabilistic uncertainty analyses convey not only model projections of policy outcomes, but also quantification of confidence in the projections. e, As policies are adopted and the microbiological system is influenced accordingly, the model can be iteratively updated to reflect the shifting status quo, thereby progressively optimizing policies within an evolving system.

Full size image

Ebola virus outbreaks

The 2014 Ebola virus outbreak struck a populous region near the border of Guinea and Sierra Leone, sparking a crisis in a resource-constrained area that had no prior experience with the virus. As the caseload mounted and disseminated geographically, it became apparent that the West African outbreak would be unprecedented in its devastation. Models were developed to estimate the potential size of the epidemic in the absence of intervention, demonstrating the urgent need for expanded action by the international community34,35,36, and to calculate the scale of the required investment37. Initial control efforts included a militarily enforced quarantine of a Liberian neighbourhood in which Ebola was spreading. Modelling analysis in collaboration with the Liberian Ministry of Health demonstrated that the quarantine was ineffective and possibly even counterproductive38. Connecting the microbiological and population scales, another modelling study integrated within-host viral load data over the course of Ebola infection and between-host transmission parameterized by contact-tracing data. The resulting dynamics highlighted the imperative to hospitalize most cases in isolation facilities within four days of symptom onset39. These modelling predictions were borne out of empirical observations. Early in the outbreak, when the incidence was precipitously growing, the average time to hospitalization in Liberia was above six days40. As contact tracing improved, the concomitant acceleration in hospitalization was found to be instrumental in turning the tide on the outbreak40. In another approach, phylogenetic analysis and transmission modelling were combined to estimate underreporting rates and social clustering of transmission41. This study informed public health authorities regarding the optimal scope and targeting of their efforts, which were central to stemming the epidemic.

Although data can be scarce for emerging pathogens, modellers can exploit similarities with better-characterized disease systems to investigate the potential efficiency of different interventions (Box 1). As vaccine candidates became available against Ebola, ring vaccination was proposed based on the success of the strategy in eliminating smallpox42, another microorganism whose transmission required close contact between individuals and for which peak infectiousness occurs after the appearance of symptoms. Compartmental models had suggested parameter combinations for which ring vaccination would be superior to mass vaccination43, and methodological advances subsequently allowed for explicit incorporation of contact network data44. Modelling based on social and healthcare contact networks specific to West Africa supported implementation of ring vaccination45, and the approach was adopted for the clinical trial of the vaccine46.

In 2018, two independent outbreaks of Ebola erupted in the Democratic Republic of the Congo. During the initial outbreak in Équateur province, modellers combined case reports with time series from previous outbreaks to generate projections of final epidemic size that could inform preparedness planning and allocation of resources47. Ring vaccination was again deployed, this time within two weeks of detecting the outbreak. A spatial model quantified the impact of vaccine on both the ultimate burden and geographic spread of Ebola, highlighting how even one week of additional delay would have substantially reduced the ability of vaccination to contain this outbreak48. The second outbreak was reported in August in the North Kivu province. Armed conflict in this region has interfered with the ability of healthcare workers to conduct the necessary contact tracing, vaccination and treatment. As conditions make routine data collection difficult and even dangerous, modelling has the potential to provide crucial insights into the otherwise unobservable characteristics of this outbreak.

Pandemic influenza

In contrast to the unexpected emergence of Ebola in a new setting, the influenza virus has repeatedly demonstrated its ability to cause pandemics. A pandemic is an event in which a pathogen creates epidemics across the entire globe. The 1918 pandemic killed an estimated 50 million people worldwide49, exceeding the combined military and civilian casualties of World War 1. While the 2% case-fatality rate of the 1918 strain was approximately 40 times higher than is typical for influenza50, pathogenic strains with case-fatality rates exceeding 50% periodically emerge51. Modelling has illustrated how repeated zoonotic introductions impose selection for elevated human-to-human transmissibility, which thereby exacerbates the threat of a devastating influenza pandemic52. Such threats underscore the importance of surveillance systems and preparedness plans, which can be informed by modelling (Box 1). Transmission models are able to optimize surveillance systems, accelerate outbreak detection and improve forecasting53,54,55,56. For example, a spatial model integrating a variety of surveillance data streams and embedded in a user-friendly platform is currently implemented by the Texas Department of State Health Services to generate real-time influenza forecasts (http://flu.tacc.utexas.edu/). Modelling has also motivated the development of dynamic preparedness plans, which adapt in response to the unfolding events of a pandemic, as models identified that adaptive efforts would be more likely to contain an influenza pandemic than static policies chosen a priori57. Other pandemic influenza analyses used age-structured compartmental models to study the trade-off between targeting influenza vaccination to groups that transmit many infections but experience relatively low health burdens (for example, schoolchildren) versus groups that transmit fewer infections but experience greater health burdens (for example, the elderly)58. Such examples illustrate the insights that modelling has provided to the decision makers charged with maintaining readiness against simultaneously rare but catastrophic situations.

Vaccine hesitancy

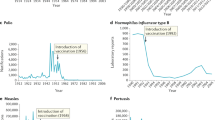
Modelling has also examined the impact of human behaviour, including vaccination decisions and social interactions, on the course of an epidemic. Public health interventions are not always sufficient to ensure disease control, as behavioural factors can thwart progress59,60,61,62. For example, reports in 1974 of potential neurological side effects from the whole-cell pertussis vaccine led to a steep decline in vaccine uptake throughout the UK, followed by a slow recovery (Fig. 2a)63. Vaccine uptake ebbed and flowed over the next two decades, with higher rates of vaccination in the wake of large pertussis outbreaks (Fig. 2b)61,63. Compartmental models analysing the interplay between vaccine uptake and disease dynamics confirmed the hypothesis that increases in vaccination were a response to the pertussis infection risk61, and showed that incorporating this interplay can improve epidemiological forecasts. Network models extending these coupled disease–behaviour analyses have illustrated how the perceived risk of vaccination can have greater influence on vaccine uptake than disease incidence64.

More recently, vaccine refusal has led to the resurgence of measles in the USA62,65. Researchers are turning to social media to gather information about attitudes toward vaccines and infectious diseases, and to glean clues about vaccinating behaviour55,66,67. For instance, signals that vaccine refusal is compromising elimination can be detected months or years in advance of disease resurgence by applying mathematical analysis of tipping points to social media data that have been classified on the basis of sentiment using machine learning algorithms66. These and other data science techniques might help public health authorities identify the specific communities that are at increased risk of future outbreaks. On shorter timescales, the near-instantaneous availability of social media data facilitates its integration into models developed for outbreak response55,66. Other behavioural factors that have been incorporated into transmission models include attendance at social gatherings, sexual behaviour and commuting patterns—elements which are also often affected by perceived infection risk59,68,69.

Antimicrobial resistance

A substantial portion of the increase in human lifespan over the last century is attributable to antibiotics70, but the emergence of pathogen strains that are resistant to antimicrobials threatens to reverse these gains. The extensive use and misuse of antibiotics has led to the evolution of multidrug-resistant, extensively drug-resistant and even pan-drug-resistant pathogens across the globe. Precariously, this evolution outpaces the development of new antibiotics.

Mathematical modelling is being used to identify strategies to forestall the emergence and re-emergence of antimicrobial resistance71,72. Models are particularly valuable for comparing alternative strategies, such as administration of different antibiotics within the same hospital ward, temporal cycling of antibiotics and combination therapy73,74,75,76. High-performance computing now permits the rapid exploration of multidimensional parameter space. Models can thereby narrow an array of possible interventions down to a subset likely to have the highest impact or optimize between trade-offs, such as effectiveness and cost (Box 1). By contrast, expense, feasibility and ethical considerations may impose more limitations on in vivo investigations (Box 1). Not only can models identify the optimal strategy for a given parameter set, but they can generate the probability that this intervention remains optimal across variation in the parameters. For example, an optimization routine combined with simulation of hospital-based interventions identified combination therapy as most likely to reduce antibiotic resistance75. As a complementary approach, modelling can incorporate economic considerations into these evaluations. A stochastic compartmental model showed that infection control specialists dedicated to promoting hand hygiene in hospitals are cost-effective for limiting the spread of antibiotic resistance74.

Although most models of antibiotic resistance have focused on transmission in healthcare settings, the importance of antibiotic resistance in natural, agricultural and urban settings has been increasingly recognized77,78,79,80,81,82,83. For example, a metapopulation model of antimicrobial-resistant Clostridium difficile simulated its transmission within and between hospitals, long-term care facilities and the community. This model demonstrated that mitigating risk in the community has the potential to substantially avert hospital-onset cases by decreasing the number of patients with colonization at admission and thereby the transmission within hospitals84. This study illustrates how models can consider the entire ecosystem of infection to elucidate dynamics that might not be captured through focus on a single setting.

Sensitivity and uncertainty analysis

During the initial phase of an outbreak, the predictive power of models is often constrained by data scarcity. This challenge is exacerbated for outbreaks of novel emerging diseases given that our understanding of the disease will rely on the unfolding epidemic (Fig. 1). Not only can the absence of data constrain model design, but sparse data requires extensive sensitivity analyses to evaluate the robustness of conclusions. Univariate sensitivity analyses, in which individual parameters are varied incrementally above and below a point estimate, can identify which parameters most influence model output (Box 1). Such comparisons reveal both salient gaps in knowledge and targets for preventing and mitigating the outbreak (Box 1)85. As an outbreak progresses, each day has the potential to provide more information about the new disease, including its duration of latency, the symptomatic period, infectiousness, transmission modalities, underreporting and the case-fatality rate. However, collecting detailed data to inform each of these parameters can strain resources when they are thinly spread during an emergency response. Sensitivity analysis can support clinicians and epidemiologists in prioritizing data collection efforts86.

Parameterization challenges are compounded for complicated disease systems, such as vector-borne diseases. For example, models of Zika virus infection span both species and scales, as the disease trajectory is influenced by factors ranging from mosquito seasonality and mosquito abundance down to viral and immunological dynamics within human and mosquito hosts87,88. Adding to this complexity, the ecological parameters vary seasonally and geographically—heterogeneities that may be amplified by socioeconomic factors modulating human exposure to infected mosquitoes89. In the absence of the high-resolution data that would be ideal to tailor a mosquito-driven disease system to a given setting, uncertainty analysis can unify parameterization from disparate data sources. In contrast to univariate sensitivity analyses, uncertainty analysis simultaneously samples from empirical- or expert-informed distributions for many or all input parameters. Collaboration between modellers and disease experts is thus instrumental to ensuring the biological plausibility of these parameter distributions90,91. The uncertainty analysis produces both a central point estimate and a range for each outcome, a combination which can inform stakeholders about the best-case and worst-case scenarios as well as the likelihood that an intervention will be successful92,93,94.

Pitfalls and how to avoid them

In constructing models and communicating results, there are common pitfalls which can compromise the rigor and impact of the research.

A pervasive pitfall is the incorporation of excessive model complexity, particularly through inclusion of more parameters than can be reliably parameterized from data. Intuition might suggest that a complex representation of a microbiological system would more closely represent reality. However, the predictive power of a model can be degraded if incorporating additional parameters only marginally improves the fit to data. This tendency results in complicated transmission models that overfit data in much the same way that complicated statistical regressions can overfit data, replicating not only the relevant trends but also the noise in a particular data set. These overfit models thus become less useful for prediction and generalization6,95.

To guide appropriate model complexity and parameterization, modellers have used the mathematical theory of information to develop criteria which quantify the balance between realism and simplicity. Such criteria penalize additional parameters but reward substantial improvements in fit, thereby identifying the simplest model that can adequately fit the data61,96,97. These methods can be applied to select among models or alternatively to calculate weighted average predictions across models. In a similar vein, modelling consortiums serve to address uncertainty surrounding model design98,99,100. In a consortium, several modelling groups develop their models independently, each applying their particular expertise and perspective. For example, consortia of malaria modellers were convened to predict the effectiveness of interventions, including a vaccine candidate101 and mass drug administration102. Congruence of output among models engenders confidence that model results are robust.

Another pitfall concerns the quality of data used to inform the model. Incompleteness of data has been an issue since 1766, when Daniel Bernoulli published a compartmental model of smallpox and acknowledged that more extended analyses would have been possible if the data had been age-stratified103. Even today, using data to develop models without knowledge of how the data were collected or the limitations of the data can be risky. Data collected for an alternative purpose can contain gaps or biases that are acceptable for the original research question, yet lead to incorrect conclusions when incorporated for another purpose in a specific model. In ideal circumstances, modellers would be involved in the design of the original study, ensuring both seamless integration of the results into the model and awareness on the part of the modeller with regard to data limitations. Failing that, it is very helpful for modellers to collaborate with scientists familiar with the details of empirical studies on which their results might depend.

This lack of familiarity with the biases or incompleteness of data sources may be particularly dangerous in the era of digital data. ‘Big data hubris’ can blind researchers to the limitations of the dataset, such as being a large but unrepresentative sample of the general population, or the alteration of search engine algorithms partway through the data collection process6. Some of these limitations can be addressed by using digital data as a complement to traditional data sources. In this way, the weakness of one data source (for example, low sample size of traditional surveys or bias in large digital data) can be compensated by the strengths of another data source (for example, balanced representation in small survey versus large scale of digital data).

A final pitfall that often arises in the midst of an ongoing outbreak concerns the interpretation of epidemic projections. Initial models may assume an absence of intervention as a way to assess the potential consequences of inaction. Such projections may contribute to the mobilization of government resources towards control, as was the case during the West African Ebola outbreak35,37,38. In this respect, the projections are intended to make themselves obsolete104. In retrospect and without knowledge of the initial purpose of the model, it may appear that the initial predictions were excessively pessimistic105. Additionally, people living in outbreak zones often change their behaviour to reduce infection risks, thereby mitigating disease spread through, for example, reducing social interactions or increasing vaccine uptake (Fig. 2)59,61,66. Thus, risk assessment constitutes a ‘moving target’105. For example, input parameters estimated from contact tracing early in an outbreak could require adjustments to reflect these behaviour changes and accurately predict subsequent dynamics106.

Fig. 2: Behavioural changes drive outbreak patterns and also respond to them.
figure 2

a, Pertussis case notifications, pertussis deaths and the percentage of children completing the full course of vaccines by their second birthday in England and Wales, 1968–2000. A case series describing children with suspected neurological damage from the whole-cell pertussis vaccine was published in 1974 and received widespread media attention. Subsequently, the National Childhood Encephalopathy Study published in 1981 clarified the risks, which motivated public health efforts to boost vaccine uptake. The whole-cell pertussis vaccine was replaced with an acellular formulation in 1996. b, Pertussis case notifications and percentage change in vaccine uptake in successive years during the recovery phase, 1977–1994. Vaccine uptake appears to be entrained by surges in infection incidence. Mathematical models can capture the interplay between natural and human dynamics exemplified in this dataset and a wide variety of other study systems.

Full size image

The need for proficient communication skills is heightened during an outbreak. This concern is particularly relevant when presenting sensitivity and uncertainty analyses. Although predictions at the extreme of sensitivity analyses also tend to be less probable than mid-range projections, there can be a temptation to focus on the most sensational model scenarios. Ensuing public pressure on the basis of misunderstood findings can cause unwarranted alarm and trigger counterproductive political decisions. In both publications and media interactions, underscoring the improbability of extreme scenarios explored during sensitivity analysis, as well as how improved interventions turn a predictive model into a counterfactual one, may pre-empt this pitfall33.

Conclusion

The role for modelling in supporting epidemiologists, public health officials and microbiologists has progressively expanded since the foundational publications forty years ago, in concert with the growing abundance and granularity of data as well as the refinement of quantitative approaches. Models have now been developed for virtually every human infectious disease, as well as in many that affect animals and plants, and have been applied across the globe. Interdisciplinary collaboration among empiricists, policymakers and modellers facilitates the development of scientifically grounded models for specific settings and generates results that will be actionable in the real world. Reciprocally, modelling results may guide the design of experiments and field studies by revealing key gaps in our understanding of microbiological systems. Furthermore, modelling is a feasible and cost-effective approach for identifying impactful policies prior to implementation decisions. Through all these avenues, epidemiological modelling galvanizes evidence-based action to alleviate disease burden and improve global health.