Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Axion optical induction of antiferromagnetic order

Nature Materials volume 22, pages 583–590 (2023)Cite this article

Subjects

This article has been updated

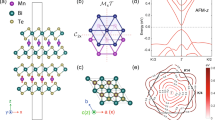
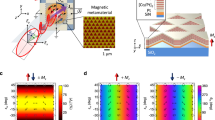
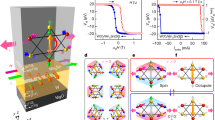
Abstract

Using circularly polarized light to control quantum matter is a highly intriguing topic in physics, chemistry and biology. Previous studies have demonstrated helicity-dependent optical control of chirality and magnetization, with important implications in asymmetric synthesis in chemistry; homochirality in biomolecules; and ferromagnetic spintronics. We report the surprising observation of helicity-dependent optical control of fully compensated antiferromagnetic order in two-dimensional even-layered MnBi2Te4, a topological axion insulator with neither chirality nor magnetization. To understand this control, we study an antiferromagnetic circular dichroism, which appears only in reflection but is absent in transmission. We show that the optical control and circular dichroism both arise from the optical axion electrodynamics. Our axion induction provides the possibility to optically control a family of \({{{\mathcal{PT}}}}\)-symmetric antiferromagnets (\({{{\mathcal{P}}}}\), inversion; \({{{\mathcal{T}}}}\), time-reversal) such as Cr2O3, even-layered CrI3 and possibly the pseudo-gap state in cuprates. In MnBi2Te4, this further opens the door for optical writing of a dissipationless circuit formed by topological edge states.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Helicity-dependent optical control of quantum matter and introduction to MnBi2Te4.
Fig. 2: Optical induction in a 2D topological antiferromagnet.
Fig. 3: Unique reflection and transmission properties and observation of the axion CD.
Fig. 4: Observation of the axion induction.
Fig. 5: Optical creation of AFM domain wall by double axion induction.
Fig. 6: Direct optical switch of AFM order by ultrafast pulse with circular polarization.

Similar content being viewed by others

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

Change history

  • 21 March 2023

    In the version of this article initially published online, there were conversion errors in the mathematical expressions and symbols in the Extended Data Figure captions, which are now restored in the HTML and PDF versions of the article.

References

  1. Basov, D., Averitt, R. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).

    Article  CAS  Google Scholar 

  2. Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).

    Article  CAS  Google Scholar 

  3. Němec, P., Fiebig, M., Kampfrath, T. & Kimel, A. V. Antiferromagnetic opto-spintronics. Nat. Phys. 14, 229–241 (2018).

    Article  Google Scholar 

  4. Kirilyuk, A., Kimel, A. V. & Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).

    Article  Google Scholar 

  5. Manz, S. et al. Reversible optical switching of antiferromagnetism in TbMnO3. Nat. Photon. 10, 653–656 (2016).

    Article  CAS  Google Scholar 

  6. Higuchi, T. & Kuwata-Gonokami, M. Control of antiferromagnetic domain distribution via polarization-dependent optical annealing. Nat. Commun. 7, 10720 (2016).

    Article  CAS  Google Scholar 

  7. Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 38, R123–R152 (2005).

    Article  CAS  Google Scholar 

  8. Jiang, S., Shan, J. & Mak, K. F. Electric-field switching of two-dimensional van der Waals magnets. Nat. Mater. 17, 406–410 (2018).

    Article  CAS  Google Scholar 

  9. Gao, A. et al. Layer Hall effect in a 2D topological axion antiferromagnet. Nature 595, 521–525 (2021).

    Article  CAS  Google Scholar 

  10. Huck, N. P., Jager, W. F., De Lange, B. & Feringa, B. L. Dynamic control and amplification of molecular chirality by circular polarized light. Science 273, 1686–1688 (1996).

    Article  CAS  Google Scholar 

  11. Xu, S.-Y. et al. Spontaneous gyrotropic electronic order in a transition-metal dichalcogenide. Nature 578, 545–549 (2020).

    Article  CAS  Google Scholar 

  12. Krichevtsov, B., Pavlov, V., Pisarev, R. & Gridnev, V. Spontaneous non-reciprocal reflection of light from antiferromagnetic Cr2O3. J. Phys. Condens. Matter 5, 8233–8244 (1993).

    Article  CAS  Google Scholar 

  13. Krichevtsov, B., Pavlov, V., Pisarev, R. & Gridnev, V. Magnetoelectric spectroscopy of electronic transitions in antiferromagnetic Cr2O3. Phys. Rev. Lett. 76, 4628–4631 (1996).

    Article  CAS  Google Scholar 

  14. Xia, J. et al. Polar Kerr-effect measurements of the high-temperature YBa2Cu3O6+x superconductor: evidence for broken symmetry near the pseudogap temperature. Phys. Rev. Lett. 100, 127002 (2008).

    Article  Google Scholar 

  15. Otrokov, M. M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416–422 (2019).

    Article  CAS  Google Scholar 

  16. Otrokov, M. M. et al. Unique thickness-dependent properties of the van der Waals interlayer antiferromagnet MnBi2Te4 films. Phys. Rev. Lett. 122, 107202 (2019).

    Article  CAS  Google Scholar 

  17. Li, J. et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 5, eaaw5685 (2019).

    Article  CAS  Google Scholar 

  18. Zhang, D. et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).

    Article  CAS  Google Scholar 

  19. Zhang, R.-X., Wu, F. & Das Sarma, S. Möbius insulator and higher-order topology in MnBi2nTe3n+1. Phys. Rev. Lett. 124, 136407 (2020).

    Article  CAS  Google Scholar 

  20. Liu, Z. & Wang, J. Anisotropic topological magnetoelectric effect in axion insulators. Phys. Rev. B 101, 205130 (2020).

    Article  CAS  Google Scholar 

  21. Deng, Y. et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 367, 895–900 (2020).

    Article  CAS  Google Scholar 

  22. Liu, C. et al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat. Mater. 19, 522–527 (2020).

    Article  CAS  Google Scholar 

  23. Deng, H. et al. High-temperature quantum anomalous Hall regime in a MnBi2Te4/Bi2Te3 superlattice. Nat. Phys. 17, 36–42 (2021).

    Article  CAS  Google Scholar 

  24. Yang, S. et al. Odd-even layer-number effect and layer-dependent magnetic phase diagrams in MnBi2Te4. Phys. Rev. X 11, 011003 (2021).

    CAS  Google Scholar 

  25. Ovchinnikov, D. et al. Intertwined topological and magnetic orders in atomically thin Chern insulator MnBi2Te4. Nano Lett. 21, 2544–2550 (2021).

    Article  CAS  Google Scholar 

  26. Cai, J. et al. Electric control of a canted-antiferromagnetic Chern insulator. Nat. Commun. 13, 1668 (2022).

    Article  CAS  Google Scholar 

  27. Li, Y. et al. Nonlocal transport and one-dimensional conduction in the axion insulator state of MnBi2Te4. Preprint at https://arxiv.org/abs/2105.10390 (2021).

  28. Tai, L. et al. Distinguishing two-component anomalous Hall effect from topological Hall effect in magnetic topological insulator MnBi2Te4. ACS Nano 16, 17336–17346 (2022).

    Article  CAS  Google Scholar 

  29. Orenstein, J. Optical nonreciprocity in magnetic structures related to high-Tc superconductors. Phys. Rev. Lett. 107, 067002 (2011).

    Article  CAS  Google Scholar 

  30. Varma, C. Gyrotropic birefringence in the underdoped cuprates. Europhys. Lett. 106, 27001 (2014).

    Article  Google Scholar 

  31. Huang, B. et al. Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 13, 544–548 (2018).

    Article  CAS  Google Scholar 

  32. Canright, G. & Rojo, A. Ellipsometry and broken time-reversal symmetry in the high-temperature superconductors. Phys. Rev. B 46, 14078 (1992).

    Article  CAS  Google Scholar 

  33. Ahn, J., Xu, S.-Y. & Vishwanath, A. Theory of optical axion electrodynamics and application to the Kerr effect in topological antiferromagnets. Nat. Commun. 13, 7615 (2022).

    Article  CAS  Google Scholar 

  34. Malashevich, A. & Souza, I. Band theory of spatial dispersion in magnetoelectrics. Phys. Rev. B 82, 245118 (2010).

    Article  Google Scholar 

  35. Graham, E. & Raab, R. Macroscopic theory of reflection from antiferromagnetic Cr2O3. J. Phys. Condens. Matter 9, 1863–1869 (1997).

    Article  CAS  Google Scholar 

  36. Dzyaloshinskii, I. & Papamichail, E. Nonreciprocal optical rotation in antiferromagnets. Phys. Rev. Lett. 75, 3004–3007 (1995).

    Article  CAS  Google Scholar 

  37. Xia, J., Maeno, Y., Beyersdorf, P. T., Fejer, M. & Kapitulnik, A. High resolution polar Kerr effect measurements of Sr2RuO4: evidence for broken time-reversal symmetry in the superconducting state. Phys. Rev. Lett. 97, 167002 (2006).

    Article  Google Scholar 

  38. Schemm, E., Gannon, W., Wishne, C., Halperin, W. & Kapitulnik, A. Observation of broken time-reversal symmetry in the heavy-fermion superconductor UPt3. Science 345, 190–193 (2014).

    Article  CAS  Google Scholar 

  39. Hayes, I. et al. Multicomponent superconducting order parameter in UTe2. Science 373, 797–801 (2021).

    Article  CAS  Google Scholar 

  40. Kawabata, K., Ashida, Y., Katsura, H. & Ueda, M. Parity-time-symmetric topological superconductor. Phys. Rev. B 98, 085116 (2018).

    Article  CAS  Google Scholar 

  41. Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).

    Article  Google Scholar 

  42. Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).

    Article  Google Scholar 

  43. Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).

    Article  CAS  Google Scholar 

  44. Xiao, D. et al. Realization of the axion insulator state in quantum anomalous Hall sandwich heterostructures. Phys. Rev. Lett. 120, 056801 (2018).

    Article  CAS  Google Scholar 

  45. Nenno, D. M., Garcia, C. A., Gooth, J., Felser, C. & Narang, P. Axion physics in condensed-matter systems. Nat. Rev. Phys. 2, 682–696 (2020).

    Article  Google Scholar 

  46. Mogi, M. et al. Experimental signature of the parity anomaly in a semi-magnetic topological insulator. Nat. Phys. 18, 390–394 (2022).

    Article  CAS  Google Scholar 

  47. Yan, J.-Q. et al. Crystal growth and magnetic structure of MnBi2Te4. Phys. Rev. Mater. 3, 064202 (2019).

    Article  CAS  Google Scholar 

  48. Zhao, S. Y. F. et al. Emergent interfacial superconductivity between twisted cuprate superconductors. Preprint at arXiv https://doi.org/10.48550/arXiv.2108.13455 (2021).

  49. Thiel, L. et al. Probing magnetism in 2D materials at the nanoscale with single-spin microscopy. Science 364, 973–976 (2019).

    Article  CAS  Google Scholar 

  50. Kimura, K., Katsuyoshi, T., Sawada, Y., Kimura, S. & Kimura, T. Imaging switchable magnetoelectric quadrupole domains via nonreciprocal linear dichroism. Commun. Mater. 1, 39 (2020).

    Article  Google Scholar 

  51. Toledano, J.-C. & Toledano, P.The Landau Theory of Phase Transitions: Application to Structural, Incommensurate, Magnetic and Liquid Crystal Systems (World Scientific, 1987).

  52. Otrokov, M. M. et al. Unique thickness-dependent properties of the van der Waals interlayer antiferromagnet MnBi2Te4 films. Phys. Rev. Lett. 122, 107202 (2019).

    Article  CAS  Google Scholar 

  53. Ahn, J., Guo, G.-Y., Nagaosa, N. & Vishwanath, A. Riemannian geometry of resonant optical responses. Nat. Phys. 18, 290–295 (2022).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

We gratefully thank X. Xu and T. Song for sharing their experience on CD set-up and M. Fiebig for providing the Cr2O3 bulk crystals. We also thank Y. Gao, B. I. Halperin, P. Hosur and P. Kim for helpful discussions. Work in the S.-Y.X. group was supported through National Science Foundation (NSF) CAREER grant no. DMR-2143177 (Harvard fund 129522). S.-Y.X. acknowledges the Corning Fund for Faculty Development. S.-Y.X., J.A., Q.M. and A.V. acknowledge support from the Center for the Advancement of Topological Semimetals, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science through the Ames Laboratory under contract DE-AC0207CH11358. The sample fabrication in the QM group was supported by the NSF Career DMR-2143426 and the (CIFAR) Azrieli Global Scholars program.C.T. acknowledges support from the Swiss National Science Foundation under project P2EZP2_191801. Y.-F.L., S.-Y.X. and D.C.B. were supported by the Science and Technology Center for Integrated Quantum Materials, NSF grant no. DMR-1231319. This work was performed in part at the Center for Nanoscale Systems at Harvard University, a member of the National Nanotechnology Coordinated Infrastructure Network, which is supported by the NSF under award no. 1541959. Work at University of California, Los Angeles was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under award no. DE-SC0021117. The work at Tata Institute of Fundamental Research Mumbai is supported by the Department of Atomic Energy of the government of India under project no. 12-R&D-TFR-5.10-0100. The work at Northeastern University was supported by the US Air Force Office of Scientific Research under award no. FA9550-20-1-0322, and it benefited from the computational resources of Northeastern University’s Advanced Scientific Computation Center and the Discovery Cluster. H.L. acknowledges the support by the National Science and Technology Council in Taiwan under grant no. MOST 111-2112-M-001-057-MY3. T.-R.C. was supported by the 2030 Cross-Generation Young Scholars Program from the National Science and Technology Council in Taiwan (programme no. MOST 111-2628-M-006-003-MY3); National Cheng Kung University, Taiwan; and National Center for Theoretical Sciences, Taiwan. This research was supported, in part, by the Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement at National Cheng Kung University. H.-Z.L. was supported by the National Key R&D Program of China (2022YFA1403700), the National Natural Science Foundation of China (11925402), Guangdong province (2016ZT06D348, 2020KCXTD001), the Science, Technology and Innovation Commission of Shenzhen Municipality (ZDSYS20170303165926217, JCYJ20170412152620376, KYTDPT20181011104202253) and the Center for Computational Science and Engineering of SUSTech. K.W. and T.T. acknowledge support from Japan Society for the Promotion of Science KAKENHI (grant nos 19H05790, 20H00354 and 21H05233). X.-Y.Z., Y.-X.W. and B.B.Z. acknowledge support from NSF award no. ECCS-2041779.

Author information

Authors and Affiliations

  1. Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA, USA

    Jian-Xiang Qiu, Christian Tzschaschel, Anyuan Gao, Houchen Li, Yu-Fei Liu, Damien Bérubé, Thao Dinh, Sheng-Chin Ho & Su-Yang Xu

  2. Department of Physics, Harvard University, Cambridge, MA, USA

    Junyeong Ahn, Yu-Fei Liu, Thao Dinh & Ashvin Vishwanath

  3. Department of Physics, Boston College, Chestnut Hill, MA, USA

    Xin-Yue Zhang, Yu-Xuan Wang, Brian B. Zhou & Qiong Ma

  4. Department of Physics, Northeastern University, Boston, MA, USA

    Barun Ghosh & Arun Bansil

  5. Department of Physics and Astronomy and California NanoSystems Institute, University of California, Los Angeles, CA, USA

    Chaowei Hu & Ni Ni

  6. Shenzhen Institute for Quantum Science and Engineering and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen, China

    Zhenhao Gong & Hai-Zhou Lu

  7. Quantum Science Center of Guangdong-Hong Kong-Macao Greater Bay Area (Guangdong), Shenzhen, China

    Zhenhao Gong & Hai-Zhou Lu

  8. Shenzhen Key Laboratory of Quantum Science and Engineering, Shenzhen, China

    Zhenhao Gong & Hai-Zhou Lu

  9. International Quantum Academy, Shenzhen, China

    Zhenhao Gong & Hai-Zhou Lu

  10. Department of Physics, National Cheng Kung University, Tainan, Taiwan

    Shang-Wei Lien & Tay-Rong Chang

  11. Center for Quantum Frontiers of Research and Technology (QFort), Tainan, Taiwan

    Shang-Wei Lien & Tay-Rong Chang

  12. Physics Division, National Center for Theoretical Sciences, Taipei, Taiwan

    Shang-Wei Lien & Tay-Rong Chang

  13. Department of Condensed Matter Physics and Materials Science, Tata Institute of Fundamental Research, Mumbai, India

    Bahadur Singh

  14. Research Center for Functional Materials, National Institute for Materials Science, Tsukuba, Japan

    Kenji Watanabe

  15. International Center for Materials Nanoarchitectonics, National Institute for Materials Science, Tsukuba, Japan

    Takashi Taniguchi

  16. Harvard John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, USA

    David C. Bell

  17. Center for Nanoscale Systems, Harvard University, Cambridge, MA, USA

    David C. Bell

  18. Institute of Physics, Academia Sinica, Taipei, Taiwan

    Hsin Lin

  19. Canadian Institute for Advanced Research, Toronto, Canada

    Qiong Ma

Authors
  1. Jian-Xiang Qiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christian Tzschaschel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junyeong Ahn
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Anyuan Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Houchen Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Xin-Yue Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Barun Ghosh
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Chaowei Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Yu-Xuan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Yu-Fei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Damien Bérubé
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Thao Dinh
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Zhenhao Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Shang-Wei Lien
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Sheng-Chin Ho
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Bahadur Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Kenji Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Takashi Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. David C. Bell
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. Hai-Zhou Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  21. Arun Bansil
    View author publications

    You can also search for this author in PubMed Google Scholar

  22. Hsin Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  23. Tay-Rong Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  24. Brian B. Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  25. Qiong Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  26. Ashvin Vishwanath
    View author publications

    You can also search for this author in PubMed Google Scholar

  27. Ni Ni
    View author publications

    You can also search for this author in PubMed Google Scholar

  28. Su-Yang Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.-X.Q. performed the optical measurements and analysed data with help from C.T. and H. Li; J.-X.Q. performed the transport measurements with help from A.G.; A.G. fabricated the 2D MnBi2Te4 samples with help from J.-X.Q., H. Li, Y.-F.L., D.B., T.D., S.-C.H. and Q.M.; and C.H. and N.N. grew the bulk MnBi2Te4 single crystals. J.A. and A.V. developed the theory of optical axion electrodynamics with discussions with S.-Y.X.; B.G. and J.A. made first-principles calculations with help from B.S. under the supervision of H.L., T.-R.C., A.B. and A.V.; and Z.G. and H.-Z.L. did model simulations. D.C.B. performed transmission electron microscope measurements. X.-Y.Z., Y.-X.W. and B.B.Z. performed the NV centre magnetometry experiments. K.W. and T.T. grew the bulk hBN single crystals. S.-Y.X., J.-X.Q. and Q.M. wrote the paper with input from all authors. J.-X.Q. came up with the idea of optical induction of AFM. S.-Y.X. supervised the project and was responsible for the overall direction, planning and integration among the different research units.

Corresponding authors

Correspondence to Ni Ni or Su-Yang Xu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Materials thanks Joseph Orenstein, Yong Xu and Liuyan Zhao for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Reproducible RCD measurements for nine consecutive inductions with alternating induction helicities.

a, RCD as a function of temperature while warming up after induction with σ− light. b, Same as panel (a) but after induction with σ+ light. c, Spatial mapping of the optical contrast near the 8SL MnBi2Te4 flake. The square box marks the region for induction experiments. d, RCD map after induction with opposite helicity. The circle marks the spot that is subject to the induction light while cooling; The σ+ and σ− on each small panel denotes the helicity of the induction light. Experimental parameters used for data in this figure: \({\lambda }_{induction}=840\,{\rm{nm}},\,{P}_{induction}\simeq 1\,{\rm{mW}}\); \({\lambda }_{detection}=946\,{\rm{nm}},\,{P}_{detection}\simeq 30\,\mu{\rm{W}}\). Scale bars for panels (c, d) are 2 μm.

Extended Data Fig. 2 Circular dichroism in 2D MnBi2Te4.

a, Optical contrast of sample-S2 on diamond structure, which consists of four connected flakes of 5SL, 6SL, 7SL and 8SL. b, Nitrogen vacancy center measured stray magnetic field of sample S2. c, RCD spatial mapping at B = 0 using \({\lambda }_{detection}=710\, {\rm{nm}}\). The sample was cooled down with a finite B field and the B field was ramped to zero before the measurements. d, Same as panel c but using \({\lambda }_{detection}=946\, {\rm{nm}}\). No optical induction was performed in panels c-d. Scale bars (horizontal and vertical lines) are all 5 μm. We note that the NV and CD measurements were performed in different setups. Hence the spatial mappings (b and c, d) are rotated with respect to each other. e-h, Magnetic hysteresis of RCD for 5SL, 6SL, 7SL and 8SL measured at \({\lambda }_{detection}=710\,{\rm{nm}}\). i-l, Same as panels (e-h) but measured at \({\lambda }_{detection}=946\,{\rm{nm}}\). m-p, RCD spectra at B = 0 for 5-8SL. The spectrum strongly depends on the evenness or oddness of the layer number, consistent with the different physical origins of the CDs in even and odd layers. It is interesting to note that ~ 700 nm is the symmetric (antisymmetric) point for odd (even) layers. For panels (m-p), data are presented as mean values +/- SEM (n=3).

Extended Data Fig. 3 Symmetry analysis for CD in \({\mathcal{PT}}\)-symmetric AFM.

a, σ− light transmitting through a sample. Upon \({\mathcal{PT}}\) inversion, the AFM remains invariant and the light path also stays the same, but light helicity is reversed. As such, \({\mathcal{PT}}\) enforces the transmission for σ± to be identical, which means TCD =0. b, σ− light reflecting off a sample. Upon \({\mathcal{PT}}\) inversion, the AFM remains invariant but the reflection is changed to the bottom surface. This means that \({\mathcal{PT}}\) does not impose any constraint on RCD experiments, because RCD compares the reflections of σ± lights from the same side of the sample. Carrying out the same analysis exhaustively confirms that there is no symmetry that can relate the reflections of light with opposite helicity while keeping the AFM invariant. Therefore, RCD is allowed.

Extended Data Fig. 4 RCD vs. TCD measurements of the 6SL and 8SL MnBi2Te4 in sample- S1.

a,b, RCD and TCD magnetic hysteresis measurements at 946 nm. c,d, RCD and TCD spectra at B = 0 (data are presented as mean values +/- SEM, n=3).

Extended Data Fig. 5 Intuitive picture for Axion ME coupling and Axion CD.

a, The Berry curvature causes transverse electron motion in response to an external DC E field. b, Analogously, the inter-band Berry curvature causes a transverse electron motion in response to light’s \(E^{\omega}\) field upon an interband transition. Ref. 53 provides a detailed theoretical analysis for the clear geometrical origin of the inter-band Berry curvature. c, The Berry curvature induced optical ME coupling can be visualized an itinerant electron circulation in response to electric field. Specifically, upon the application of an electric field \(E^{\omega}\), Berry curvature leads to transverse electron motion. Because of the Berry curvature at ± Z is opposite, the transverse motions of electrons at ± Z are in opposite directions. This in turn leads to an itinerant electron circulation \(J^{\omega}\), which is equivalent to magnetization \(M^{\omega}\). d,e, Rotation of electric field \(E_{0}^{\omega}\) for σ± light. f, Light’s magnetic field \(B^{\omega}\) can lead to an electric polarization \(P_{0}^{\omega}=\alpha(\omega)B_{0}^{\omega}\) through the optical ME effect, which rotates light’s electric field \(E^{\omega}\). Suppose this rotation is in the clockwise direction. Then, this additional clockwise rotation would be along the same direction as the intrinsic rotation (also clockwise) for σ± light but opposite to the intrinsic rotation (counter-clockwise) for σ− light. This provides an intuitive picture for why σ± light can behave differently in an Axion insulator, a prerequisite for nonzero CD.

Extended Data Fig. 6 Distinct mechanism for the three classes of helicity-dependent optical control.

\(({\rm{E}}^{\omega} \times {{\rm{E}}^{\omega}}^{\ast})\cdot {\hat{\rm{q}}}\), \(({\rm{E}}^{\omega} \times {{\rm{E}}^{\omega}}^{\ast})\), and \(({\rm{E}}^{\omega} \times {{\rm{E}}^{\omega}}^{\ast})\cdot {\hat{\rm{Z}}}\) (panels a-c) are symmetry-equivalent to chirality, B and E ⋅ B, respectively.

Extended Data Fig. 7 Three classes of CD in chiral crystals, ferromagnets and \({\mathcal{PT}}\)- symmetric AFM.

a-c, Chiral crystals, ferromagnets and \({\mathcal{PT}}\)-symmetric AFM feature distinct nontrivial interactions with circularly-polarized light. They can only be distinguished by their transmission and reflection properties. d-f, Equally importantly, when bands with nontrivial topology or giant Berry curvature occur in these three classes of materials, the respective CD can dominantly arise from the Berry curvature properties, namely the Berry curvature k space dipole, the total Berry curvature, and the Berry curvature real space dipole, respectively.

Supplementary information

Supplementary Information

Supplementary Sections I–V.

Reporting Summary

Source data

Source Data Fig. 1

Statistical source data.

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Fig. 5

Statistical source data.

Source Data Fig. 6

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiu, JX., Tzschaschel, C., Ahn, J. et al. Axion optical induction of antiferromagnetic order. Nat. Mater. 22, 583–590 (2023). https://doi.org/10.1038/s41563-023-01493-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41563-023-01493-5

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing