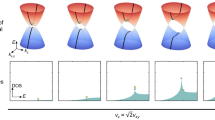
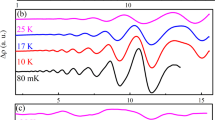
Abstract
Landau band crossings typically stem from the intra-band evolution of electronic states in magnetic fields and enhance the interaction effect in their vicinity. Here in the extreme quantum limit of topological insulator HfTe5, we report the observation of a topological Lifshitz transition from inter-band Landau level crossings using magneto-infrared spectroscopy. By tracking the Landau level transitions, we demonstrate that band inversion drives the zeroth Landau bands to cross with each other after 4.5 T and forms a one-dimensional Weyl mode with the fundamental gap persistently closed. The unusual reduction of the zeroth Landau level transition activity suggests a topological Lifshitz transition at 21 T, which shifts the Weyl mode close to the Fermi level. As a result, a broad and asymmetric absorption feature emerges due to the Pauli blocking effect in one dimension, along with a distinctive negative magneto-resistivity. Our results provide a strategy for realizing one-dimensional Weyl quasiparticles in bulk crystals.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. All other supporting data are available from the corresponding authors upon reasonable request.
References
Shoenberg, D. Magnetic Oscillations in Metals (Cambridge Univ. Press, 2009).
Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Lupatini, M. et al. Spin reversal of a quantum Hall ferromagnet at a Landau level crossing. Phys. Rev. Lett. 125, 067404 (2020).
Jungwirth, T. & MacDonald, A. H. Pseudospin anisotropy classification of quantum Hall ferromagnets. Phys. Rev. B 63, 035305 (2000).
Ferreira, G. J., Freire, H. J. P. & Egues, J. C. Many-body effects on the ρxx ringlike structures in two-subband wells. Phys. Rev. Lett. 104, 066803 (2010).
Taychatanapat, T., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Quantum Hall effect and Landau-level crossing of Dirac fermions in trilayer graphene. Nat. Phys. 7, 621–625 (2011).
Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. 17, 710–714 (2021).
Weyl, H. Gravitation and the electron. Proc. Natl Acad. Sci. USA 15, 323–334 (1929).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Xu, S. Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).
Huang, X. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Zhang, C. et al. Room-temperature chiral charge pumping in Dirac semimetals. Nat. Commun. 8, 13741 (2017).
Suzuki, T. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nat. Phys. 12, 1119–1123 (2016).
Zhang, C. et al. Quantum Hall effect based on Weyl orbits in Cd3As2. Nature 565, 331–336 (2019).
Yuan, X. et al. The discovery of dynamic chiral anomaly in a Weyl semimetal NbAs. Nat. Commun. 11, 1259 (2020).
Chen, R. Y. et al. Magnetoinfrared spectroscopy of Landau levels and Zeeman splitting of three-dimensional massless Dirac fermions in ZrTe5. Phys. Rev. Lett. 115, 176404 (2015).
Ma, Q. et al. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 13, 842–847 (2017).
Yuan, X. et al. Chiral Landau levels in Weyl semimetal NbAs with multiple topological carriers. Nat. Commun. 9, 1854 (2018).
Wu, L. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350–355 (2017).
Polatkan, S. et al. Magneto-optics of a Weyl semimetal beyond the conical band approximation: case study of TaP. Phys. Rev. Lett. 124, 176402 (2020).
Volovik, G. E. Topological Lifshitz transitions. Low. Temp. Phys. 43, 47–55 (2017).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Jiang, Y. et al. Unraveling the topological phase of ZrTe5 via magneto-infrared spectroscopy. Phys. Rev. Lett. 125, 046403 (2020).
Jiang, Y. et al. Landau-level spectroscopy of massive Dirac fermions in single-crystalline ZrTe5 thin flakes. Phys. Rev. B 96, 041101 (2017).
You, L., Zhang, Z.-Y. & Wang, Y.-X. Magneto-optic signatures in the gapped Dirac semimetal with mixed linear and parabolic dispersions of ZrTe5. New J. Phys. 23, 123033 (2021).
Wang, Y. et al. Gigantic magnetochiral anisotropy in the topological semimetal ZrTe5. Phys. Rev. Lett. 128, 176602 (2022).
Weng, H., Dai, X. & Fang, Z. Transition-metal pentatelluride ZrTe5 and HfTe5: a paradigm for large-gap quantum spin Hall insulators. Phys. Rev. X 4, 011002 (2014).
Monserrat, B. & Narayan, A. Unraveling the topology of ZrTe5 by changing temperature. Phys. Rev. Res. 1, 033181 (2019).
Morice, C., Lettl, E., Kopp, T. & Kampf, A. P. Optical conductivity and resistivity in a four-band model for ZrTe5 from ab initio calculations. Phys. Rev. B 102, 155138 (2020).
Wang, H. et al. Discovery of log-periodic oscillations in ultraquantum topological materials. Sci. Adv. 4, eaau5096 (2018).
Chen, Z.-G. et al. Spectroscopic evidence for bulk-band inversion and three-dimensional massive Dirac fermions in ZrTe5. Proc. Natl Acad. Sci. USA 114, 816–821 (2017).
Tang, F. et al. Three-dimensional quantum Hall effect and metal–insulator transition in ZrTe5. Nature 569, 537–541 (2019).
Martino, E. et al. Two-dimensional conical dispersion in ZrTe5 evidenced by optical spectroscopy. Phys. Rev. Lett. 122, 217402 (2019).
Qin, F. et al. Theory for the charge-density-wave mechanism of 3D quantum Hall effect. Phys. Rev. Lett. 125, 206601 (2020).
Zhang, C. et al. Magnetic-field-induced nonlinear transport in HfTe5. Natl Sci. Rev. https://doi.org/10.1093/nsr/nwab208 (2021).
Zhang, Y. et al. Electronic evidence of temperature-induced Lifshitz transition and topological nature in ZrTe5. Nat. Commun. 8, 15512 (2017).
Xu, B. et al. Temperature-driven topological phase transition and intermediate Dirac semimetal phase in ZrTe5. Phys. Rev. Lett. 121, 187401 (2018).
Kamm, G., Gillespie, D., Ehrlich, A., Peebles, D. & Levy, F. Fermi surface, effective masses, and energy bands of HfTe5 as derived from the Shubnikov–de Haas effect. Phys. Rev. B 35, 1223–1229 (1987).
Zhang, J. L. et al. Anomalous thermoelectric effects of ZrTe5 in and beyond the quantum limit. Phys. Rev. Lett. 123, 196602 (2019).
Cai, W. & Ting, C. S. Screening effect on the Landau-level broadening for electrons in GaAs-Ga1−xAlxAs heterojunctions. Phys. Rev. B 33, 3967–3972 (1986).
Jiang, Z. et al. Infrared spectroscopy of Landau levels of graphene. Phys. Rev. Lett. 98, 197403 (2007).
Han, X., Salehi, M., Oh, S. & Wu, L. A new type of cyclotron resonance from charge-impurity scattering in the bulk-insulating Bi2Se3 thin films. J. Phys. Appl. Phys. 55, 364004 (2022).
Akrap, A. et al. Magneto-optical signature of massless Kane electrons in Cd3As2. Phys. Rev. Lett. 117, 136401 (2016).
Mak, K. F. et al. Measurement of the optical conductivity of graphene. Phys. Rev. Lett. 101, 196405 (2008).
Abrikosov, A. A. Quantum magnetoresistance. Phys. Rev. B 58, 2788–2794 (1998).
Rodionov, Y. I., Kugel, K. I., Aronzon, B. A. & Nori, F. Effect of disorder on the transverse magnetoresistance of Weyl semimetals. Phys. Rev. B 102, 205105 (2020).
Chen, R. et al. Optical spectroscopy study of the three-dimensional Dirac semimetal ZrTe5. Phys. Rev. B 92, 075107 (2015).
Liu, Y. et al. Zeeman splitting and dynamical mass generation in Dirac semimetal ZrTe5. Nat. Commun. 7, 12516 (2016).
Galeski, S. et al. Unconventional Hall response in the quantum limit of HfTe5. Nat. Commun. 11, 5926 (2020).
Zhao, P.-L., Lu, H.-Z. & Xie, X. C. Theory for magnetic-field-driven 3D metal-insulator transitions in the quantum limit. Phys. Rev. Lett. 127, 046602 (2021).
Fu, B., Wang, H.-W. & Shen, S.-Q. Dirac polarons and resistivity anomaly in ZrTe5 and HfTe5. Phys. Rev. Lett. 125, 256601 (2020).
Choi, Y., Villanova, J. W. & Park, K. Zeeman-splitting-induced topological nodal structure and anomalous Hall conductivity in ZrTe5. Phys. Rev. B 101, 035105 (2020).
Wang, C. Thermodynamically induced transport anomaly in dilute metals ZrTe5 and HfTe5. Phys. Rev. Lett. 126, 126601 (2021).
Zheng, G. et al. Field-induced topological phase transition from a three-dimensional Weyl semimetal to a two-dimensional massive Dirac metal in ZrTe5. Phys. Rev. B 96, 121401 (2017).
Liang, T. et al. Anomalous Hall effect in ZrTe5. Nat. Phys. 14, 451–455 (2018).
Xiong, H. et al. Three-dimensional nature of the band structure of ZrTe5 measured by high-momentum-resolution photoemission spectroscopy. Phys. Rev. B 95, 195119 (2017).
Zhang, Y. et al. Temperature-induced Lifshitz transition in topological insulator candidate HfTe5. Sci. Bull. 62, 950–956 (2017).
Li, Q. et al. Chiral magnetic effect in ZrTe5. Nat. Phys. 12, 550–554 (2016).
Büttner, B. et al. Single valley Dirac fermions in zero-gap HgTe quantum wells. Nat. Phys. 7, 418–422 (2011).
Klier, J., Gornyi, I. V. & Mirlin, A. D. Transversal magnetoresistance in Weyl semimetals. Phys. Rev. B 92, 205113 (2015).
Pesin, D. A., Mishchenko, E. G. & Levchenko, A. Density of states and magnetotransport in Weyl semimetals with long-range disorder. Phys. Rev. B 92, 174202 (2015).
Xiao, X., Law, K. T. & Lee, P. A. Magnetoconductivity in Weyl semimetals: effect of chemical potential and temperature. Phys. Rev. B 96, 165101 (2017).
Könye, V. & Ogata, M. Magnetoresistance of a three-dimensional Dirac gas. Phys. Rev. B 98, 195420 (2018).
Acknowledgements
X.Y. was supported by the National Natural Science Foundation of China (grant no. 12174104, no. 62005079 and no. 62111530237), the Shanghai Sailing Program (grant no. 20YF1411700), the International Scientific and Technological Cooperation Project of Shanghai (grant no. 20520710900) and a start-up grant from East China Normal University. C.Z. was supported by the National Natural Science Foundation of China (grant no. 12174069), Shanghai Sailing Program (grant no. 20YF1402300), Natural Science Foundation of Shanghai (grant no. 20ZR1407500), the Young Scientist project of the Ministry of Education innovation platform and a start-up grant from Fudan University. H.-Z.L. was supported by the National Natural Science Foundation of China (grant no. 11925402). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation cooperative agreement no. DMR-1644779 and the State of Florida. Part of the sample fabrication was performed at Fudan Nano-fabrication Laboratory. We thank M. Orlita, M. Potemski, H. Yan, Y. Jiang, Z.-G. Chen, Z. Sun, C.-G. Duan, F. Yue, B. Tian and Y. Liu for helpful discussions.
Author information
Authors and Affiliations
Contributions
X.Y. conceived the idea and supervised the overall research. X.M., B.L. and Y.M. carried out the growth of the HfTe5 single crystals. M.O., W.W., Z.S. and Y.D. performed the magneto-infrared experiments. C.Z. and Y.W. conducted the magneto-transport experiments. W.W., X.Y., Z.Y., F.Q. and H.-Z.L. performed the theoretical analyses based on the k ⋅ p model. X.Y., W.W., C.Z., Z.S. and J.C. wrote the paper with the help of all the coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–13, Discussion Sections I–XII and Tables 1–3.
Source data
Source Data Fig. 2
Magneto-resistivity (Fig. 2a), temperature-dependent oscillation amplitude (Fig. 2c) and relative magneto-transmittance spectrum (Fig. 2e).
Source Data Fig. 3
Energy of Tα and Tβ (Fig. 3a(iv)), normalized Pauli-blocking-induced spectral weight with corresponding first-order derivative (Fig. 3a(v)) and theoretical real part of magneto-optical conductivity (Fig. 3d).
Source Data Fig. 4
Magneto-resistivity (Fig. 4e).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, W., Shi, Z., Du, Y. et al. Topological Lifshitz transition and one-dimensional Weyl mode in HfTe5. Nat. Mater. 22, 84–91 (2023). https://doi.org/10.1038/s41563-022-01364-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-022-01364-5
This article is cited by
-
The discovery of three-dimensional Van Hove singularity
Nature Communications (2024)
-
A new way to Weyl
Nature Materials (2023)