Abstract
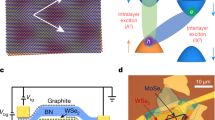
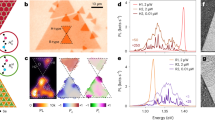
The possibility of confining interlayer excitons in interfacial moiré patterns has recently gained attention as a strategy to form ordered arrays of zero-dimensional quantum emitters and topological superlattices in transition metal dichalcogenide heterostructures. Strain is expected to play an important role in the modulation of the moiré potential landscape, tuning the array of quantum dot-like zero-dimensional traps into parallel stripes of one-dimensional quantum wires. Here, we present real-space imaging of unstrained zero-dimensional and strain-induced one-dimensional moiré patterns along with photoluminescence measurements of the corresponding excitonic emission from WSe2/MoSe2 heterobilayers. Whereas excitons in zero-dimensional moiré traps display quantum emitter-like sharp photoluminescence peaks with circular polarization, the photoluminescence emission from excitons in one-dimensional moiré potentials shows linear polarization and two orders of magnitude higher intensity. These results establish strain engineering as an effective method to tailor moiré potentials and their optoelectronic response on demand.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data represented in Figs. 1–4 are provided with the article source data. All data that support the results in this article are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Change history
15 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41563-020-0773-x
References
Yao, W., Xu, X., Liu, G.-B., Tang, J. & Yu, H. Moiré excitons: from programmable quantum emitter arrays to spin-orbit–coupled artificial lattices. Sci. Adv. 3, e1701696 (2017).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Tong, Q. et al. Topological mosaics in moiré superlattices of van der Waals heterobilayers. Nat. Phys. 13, 356–362 (2017).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Yuan, L. et al. Twist-angle-dependent interlayer exciton diffusion in WS2–WSe2 heterobilayers. Nat. Mater. 19, 617–623 (2020).
Li, W., Lu, X., Dubey, S., Devenica, L. & Srivastava, A. Dipolar interactions between localized interlayer excitons in van der Waals heterostructures. Nat. Mater. 19, 624–629 (2020).
Brotons-Gisbert, M. et al. Spin–layer locking of interlayer excitons trapped in moiré potentials. Nat. Mater. 19, 630–636 (2020).
Wu, F., Lovorn, T. & Macdonald, A. H. Topological exciton bands in moiré heterojunctions. Phys. Rev. Lett. 118, 147401 (2017).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Wang, J. et al. Optical generation of high carrier densities in 2D semiconductor heterobilayers. Sci. Adv. 5, eaax0145 (2019).
Rivera, P. et al. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotechnol. 13, 1004–1015 (2018).
Li, Y. et al. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Jauregui, L. A. et al. Electrical control of interlayer exciton dynamics in atomically thin heterostructures. Science 366, 870–875 (2019).
Wu, W. et al. Piezoelectricity of single-atomic-layer MoS2 for energy conversion and piezotronics. Nature 514, 470–474 (2014).
Lee, J. H. et al. Reliable piezoelectricity in bilayer WSe2 for piezoelectric nanogenerators. Adv. Mater. 29, 1–7 (2017).
Mcgilly, L. J. et al. Visualization of moiré superlattices. Nat. Nanotechnol. (in the press).
Liu, G. et al. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 44, 2643–2663 (2014).
Ajayi, O. et al. Approaching the intrinsic photoluminescence linewidth in transition metal dichalcogenide monolayers. 2D Mater. 4, 31011 (2017).
Raja, A. et al. Dielectric disorder in two-dimensional materials. Nat. Nanotechnol. 14, 832–837 (2019).
Yu, H., Liu, G.-B., Gong, P., Xu, X. & Yao, W. Dirac cones and Dirac saddle points of bright excitons in monolayer transition metal dichalcogenides. Nat. Commun. 5, 3876 (2014).
Yu, T. & Wu, M. W. Valley depolarization due to intervalley and intravalley electron-hole exchange interactions in monolayer MoS2. Phys. Rev. B 89, 205303 (2014).
Glazov, M. M. et al. Exciton fine structure and spin decoherence in monolayers of transition metal dichalcogenides. Phys. Rev. B 89, 201302 (2014).
Wang, J., Gudiksen, M. S., Duan, X., Cui, Y. & Lieber, C. M. Highly polarized photoluminescence and photodetection from single indium phosphide nanowires. Science 293, 1455–1457 (2001).
Lefebvre, J., Fraser, J. M., Finnie, P. & Homma, Y. Photoluminescence from an individual single-walled carbon nanotube. Phys. Rev. B 69, 75403 (2004).
Gillen, R. & Maultzsch, J. Interlayer excitons in MoSe2/WSe2 heterostructures from first principles. Phys. Rev. B 97, 1–7 (2018).
Okada, M. et al. Direct and indirect interlayer excitons in a van der Waals heterostructure of hBN/WS2/MoS2/hBN. ACS Nano 12, 2498–2505 (2018).
Liu, F., Li, Q. & Zhu, X. Direct determination of momentum-resolved electron transfer in the photoexcited van der Waals heterobilayer WS2/MoS2. Phys. Rev. B 101, 201405(R) (2020).
Rivera, P. et al. Valley-polarized exciton dynamics in a 2D semiconductor heterostructure. Science 351, 688–691 (2016).
Bi, Z., Yuan, N. F. Q. & Fu, L. Designing flat bands by strain. Phys. Rev. B 100, 35448 (2019).
Ni, Z. H. et al. Uniaxial strain on graphene: Raman spectroscopy study and band-gap opening. ACS Nano 2, 2301–2305 (2008).
Gui, G., Li, J. & Zhong, J. Band structure engineering of graphene by strain: first-principles calculations. Phys. Rev. B 78, 75435 (2008).
Guinea, F., Katsnelson, M. I. & Geim, A. K. Energy gaps, topological insulator state and zero-field quantum Hall effect in graphene by strain engineering. Nat. Phys. 6, 30–33 (2009).
Castellanos-Gomez, A. et al. Local strain engineering in atomically thin MoS2. Nano Lett. 13, 5361–5366 (2013).
He, K., Poole, C., Mak, K. F. & Shan, J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett. 13, 2931–2936 (2013).
Kou, L., Frauenheim, T. & Chen, C. Nanoscale multilayer transition-metal dichalcogenide heterostructures: band gap modulation by interfacial strain and spontaneous polarization. J. Phys. Chem. Lett. 4, 1730–1736 (2013).
Edelberg, D. et al. Approaching the intrinsic limit in transition metal diselenides via point defect control. Nano Lett. 19, 4371–4379 (2019).
Acknowledgements
The PFM imaging experiments and PL measurements were supported by the Center for Programmable Quantum Materials, an Energy Frontier Research Center funded by the US Department of Energy through grant DE-SC0019443. Sample preparation and SHG characterization were supported by the Center for Precision Assembly of Superstratic and Superatomic Solids, a Materials Science and Engineering Research Center (MRSEC) through National Science Foundation (NSF) grant DMR-1420634. The power-dependent measurements on many-body effects (Supplementary Figs. 12–14) were supported by the NSF through grant DMR-1809680. Building of the confocal PL spectrometer was supported in part by the Office of Naval Research under grant N00014-16-1-2921. D.H. acknowledges the generous support from the Simons Foundation (579913).
Author information
Authors and Affiliations
Contributions
X.Y.Z., Y.B. and L.Z. conceived this work. Y.B., L.Z., J.W. and W.W. performed the experiments. L.M., J.A., F.L., P.R. and N.R.F. participated in various stages of sample preparation and characterization. D.H. and C.F.B.L. carried out strain field analysis, with supervision from D.N.B. X.C.Y. and W.Y. carried out model Hamiltonian analysis. X.Y.Z. supervised the project, with inputs from A.P., J.H. and X.X. X.Y.Z, W.Y., X.X., J.H. and A.P. participated in the interpretation of experimental findings. X.Y.Z. and Y.B. wrote the manuscript, with inputs from all coauthors. All authors read and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
All authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Text 1–3 and Figs. S1–S24.
Source data
Source Data Fig. 1
Experimental data points of PL spectra shown in Fig. 1e.
Source Data Fig. 2
Fitting data points of the strain field shown in Fig. 2k–l.
Source Data Fig. 3
Experimental data points of PL spectra shown in Fig. 3a–e, experimental and fitting data points of linear polarization responses shown in Fig. 3f–j.
Source Data Fig. 4
Experimental and fitting data points shown in Fig. 4a–c.
Rights and permissions
About this article
Cite this article
Bai, Y., Zhou, L., Wang, J. et al. Excitons in strain-induced one-dimensional moiré potentials at transition metal dichalcogenide heterojunctions. Nat. Mater. 19, 1068–1073 (2020). https://doi.org/10.1038/s41563-020-0730-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-020-0730-8
This article is cited by
-
Tuning commensurability in twisted van der Waals bilayers
Nature (2024)
-
Heterostructures coupling ultrathin metal carbides and chalcogenides
Nature Materials (2024)
-
Room-temperature quantum emission from interface excitons in mixed-dimensional heterostructures
Nature Communications (2024)
-
Twistronics and moiré excitonic physics in van der Waals heterostructures
Frontiers of Physics (2024)
-
Unveiling strain-enhanced moiré exciton localization in twisted van der Waals homostructures
Nano Research (2024)